

基于Buck变换器的大小信号模型
描述
几个网红问题
之前的文章介绍了Buck在模拟控制中,常见的PWM调制与对应的控制方式:
谈及控制必有环路,而提到环路则会条件反射想到小信号建模。 《模拟电子技术》就曾详细介绍三极管/ MOSFET组成的放大电路其大小信号分析,对以Buck为代表的开关电源来说同理,有小信号模型也必然有大信号模型,那么:
| 问题1 | 大小信号模型各自代表了什么含义,能解决何种问题? |
|---|---|
| 问题2 | 为何一谈到环路,大家就默认使用小信号模型,而不顾物理意义涵盖更广的大信号模型? |
| 问题3 | 教科书上传统的“平均模型”存在哪些悬而未决的问题? 为何说小信号环路的“穿越频率/截止频率”要设计在开关频率的1/10-1/5范围内? |
| 问题4 | 教科书外其他建模的手段都有哪些,如何分类及和“平均模型”的相互联系? |
| 问题5 | 大信号稳定性和小信号稳定性的关系? 如何看待低频极限环振荡和次谐波振荡? |
笔者曾在大四研一入门建模的阶段被这些问题困扰,本文想继续围绕模拟控制的Buck电路,不引入任何公式,以综述性质讨论它们的答案。
大信号与小信号的关系
观察一条曲线函数f(x),位于该曲线上有一点(X0,Y0),可在该点求取微分作切线,从而实现局部的线性化,得到一条在X0处附近,小扰动范围内和原先曲线等效的直线。
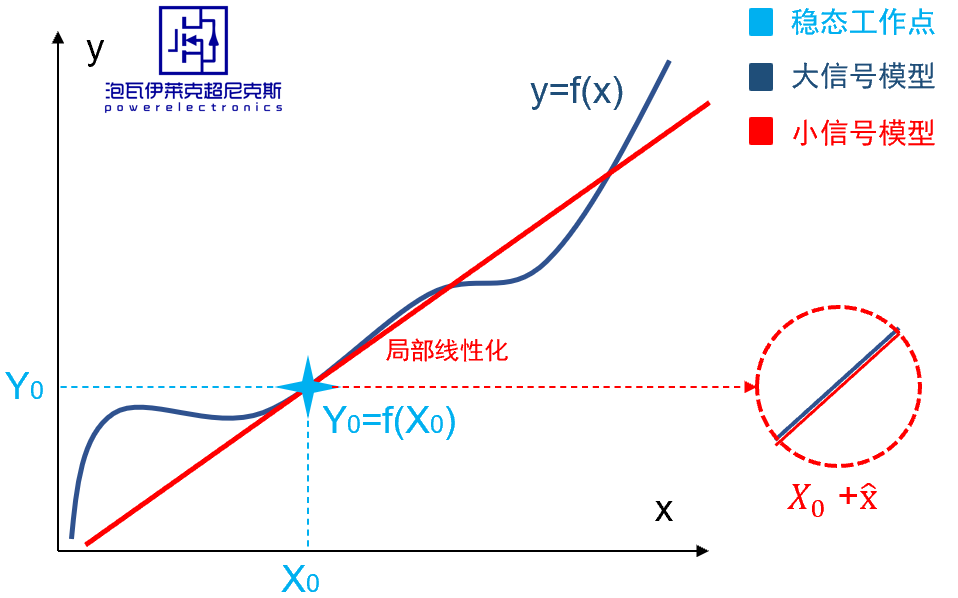
实际的开关变换器系统,包含多个状态变量和输入输出,远比一元函数复杂,但稳态工作点和大小信号的内涵是类似的。 一元函数曲线上每个点相当于每个稳态工作点,x在曲线上大幅移动相当于跨越多个稳态工作点的变工作点过程,而x停在X0处附近作小信号扰动,从而局部线性化,恰相当于在某个稳态工作点附近注入小信号扰动的输入,从而求取对应输出的,线性化的小信号模型。
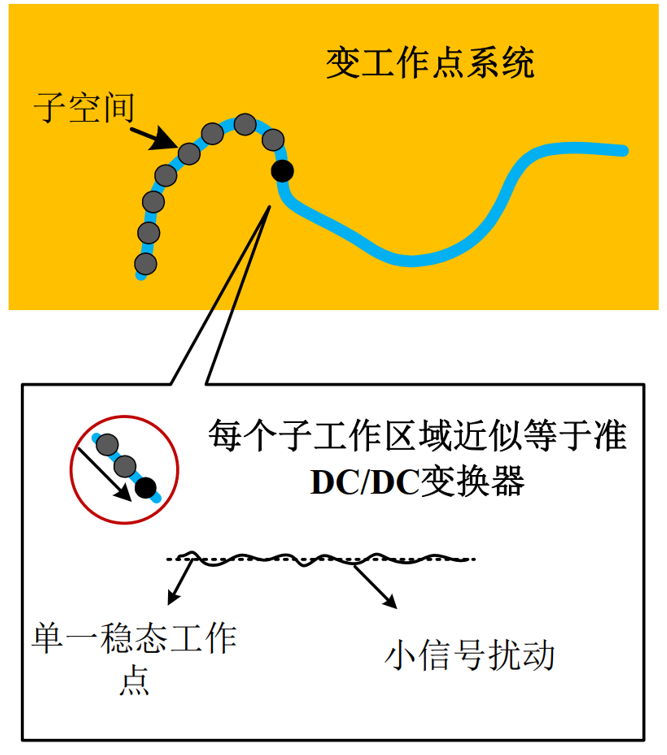
| 稳态模型 | 稳态分析(DC分析) | 描述开关电源稳定运行状态用作稳态分析 |
|---|---|---|
| 功率开关器件、储能元件及变压器等设计的基础 | ||
| 大信号模型 | 大信号分析 | 可描述大信号扰动下,开关电源变工作点(跨越多个稳态工作点)性能的非线性模型 |
| 是无数个稳态工作点的组合,在整个信号范围内均有效,能够描述全局的动力学行为和变化规律 | ||
| 小信号模型 | 小信号分析(AC分析) | 在某个稳态工作点附近注入小扰动信号,进行扰动分离和线性化处理后,得到的频率响应模型 |
由此回答 问题1和2 ,按某稳态工作点局部线性化得到的小信号模型设计的环路,严格来说只能适用于该稳态工作点附近的稳定性与动态分析,并不能用于电路有大幅波动,使得工作点偏离从而连续跨越多个稳态工作点的情况 ,如大摆幅动态,零状态启机等工况,主要原因在于不同工作点的小信号模型可能完全不同,使用同一套控制环路参数,可能导致部分工作点附近的动态表现远不及预期,甚至不稳定而发散。 这些情况应当使用大信号模型处理。
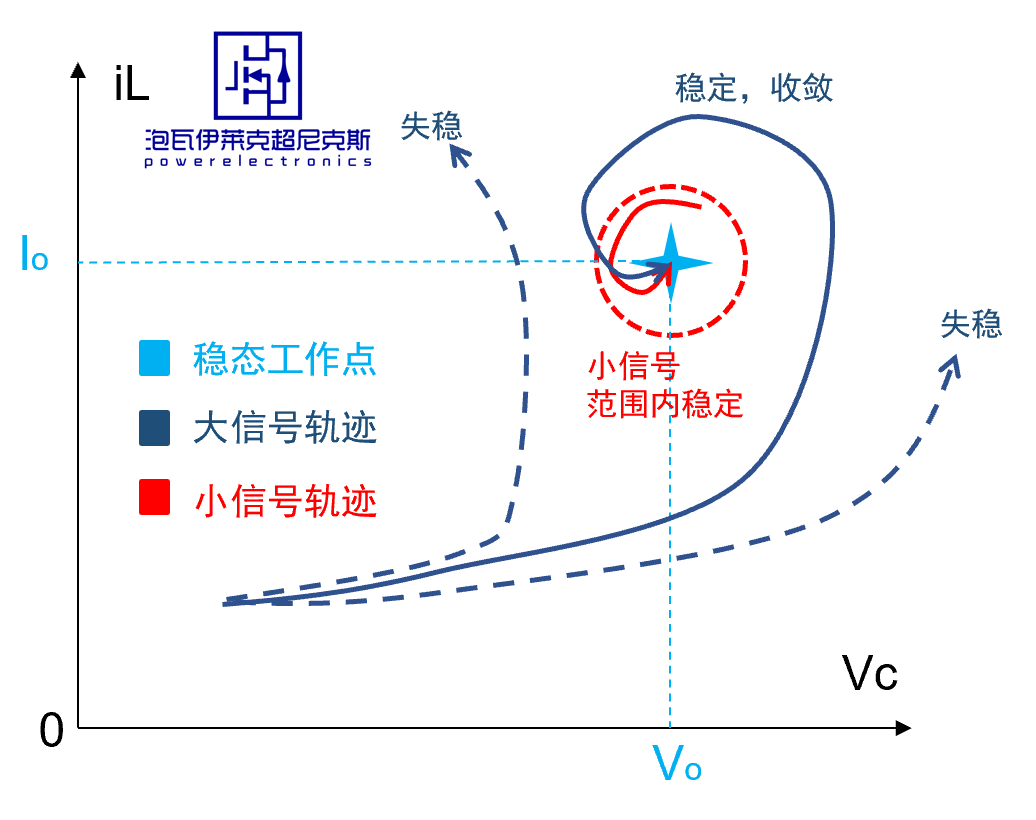
然而,为了避免处理大信号这样的非线性系统, 实际工程中只要参数设计得合理,负反馈控制系统本身就有一定的“鲁棒性”,且功率主电路的非线性并不十分强烈,使用同一套环路参数穿越多个工作点往往也是可行的,虽然一定不是最优的。
开关变换器的模型特点
针对我们最熟悉的线性时不变(LTI)系统,经典控制理论基于拉氏变换和频率特性传递函数的形式,提供了大量的分析工具,如波特图和稳定裕量判据等。 开关变换器是非线性,时变,高阶,离散,病态的系统,尤其非线性和时变这两大特点,阻碍了经典控制理论模型的建立和使用,必须找到办法逐一解决。
| 非线性 |
|---|
| 执行机构如PWM调制器,存在上下限幅行为,在大幅波动情况下特性发生改变* 每个周期中,开关管会在电阻区和截止区之间切换,需要分段解析* 元器件本身的非线性 |
| 时变 |
| PWM调制器在高频调制下,会引起时变效应 |
| 高阶 |
| 考虑杂散参数或使用含多个LC的复杂拓扑,独立储能元件个数多,存在多状态量回路 |
| 离散 |
| 开关管开和关期间,电路拓扑结构不同* PWM调制器有采样保持器特性 |
| 病态 |
| 功率主电路的“时间常数”远大于控制环路的“时间常数”,且整个系统中存在PWM控制脉冲的边沿/周期,驱动和开关脉冲的边沿/周期,电磁能量脉冲的边沿/周期,传感器采样周期,快速或慢速负载变化的边沿/周期等不同时间计量单位,是多时间尺度系统 |
传统平均模型及其缺陷
如下展示了传统的开关平均模型求取大信号模型和小信号模型手法及对应关系。
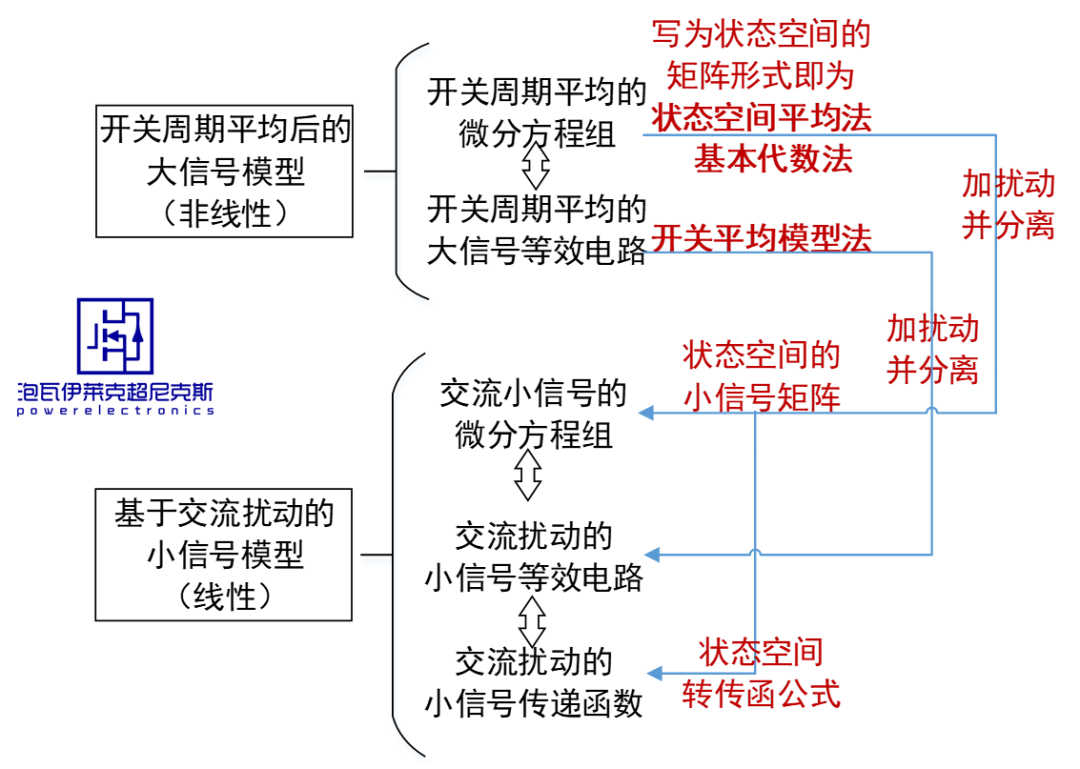
以Buck为例,为了把主电路中非线性的开关网络直接平均化,会要求满足“低频”假设和“小纹波”假设。 电路中看不到开关频率及谐波及其边频带的任何信息,从而移除开关动作造成的非线性影响。
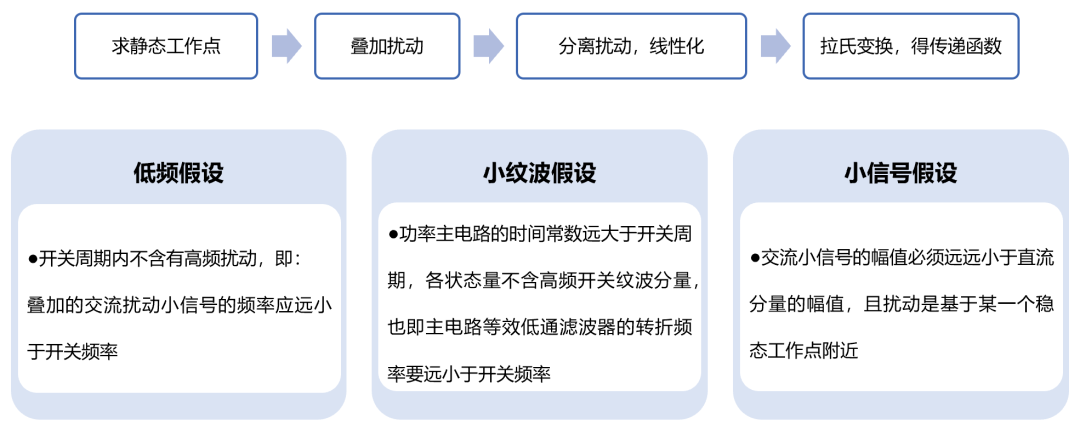
这种平均思想的代价也是显而易见的:线性化后的频率特性无法反应高频(开关频率附近)的特征。 由于环路的带宽远离开关频率,设计者对高频特性并不关心,这种假设是完全可以接受的。
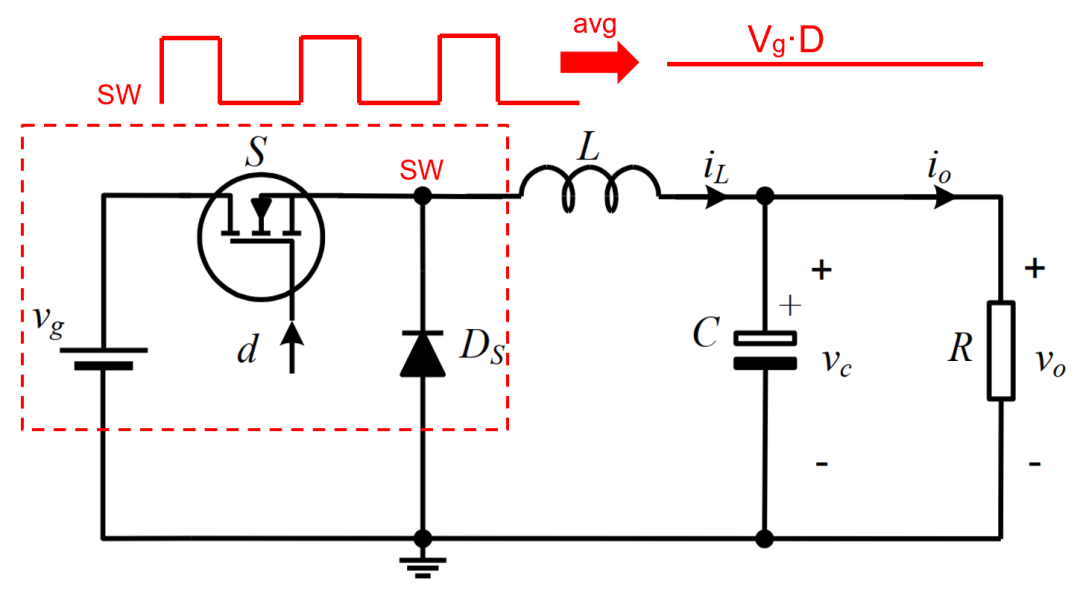
需要注意,Buck类型的变换器,包含的非线性开关网络是最容易平均简化为线性模型的,也导致了Buck类平均模型导出的小信号模型与稳态工作点无关,其他拓扑势必会更加复杂。
上述均是针对功率主电路中的非线性开关网络的,并未包含PWM调制器的处理。 除非是一个完全由方波发生器产生PWM而开环运行,一个闭环控制的环路必包含PWM调制器的模型。
下图描述了“基于平均值的比较行为”的PWM调制器,这种最基本的调制方式可直接对应到单电压环模式/平均电流模式。 图中红色信号verr为补偿器的输出作为调制波,蓝色信号为开关频率的载波vsaw。
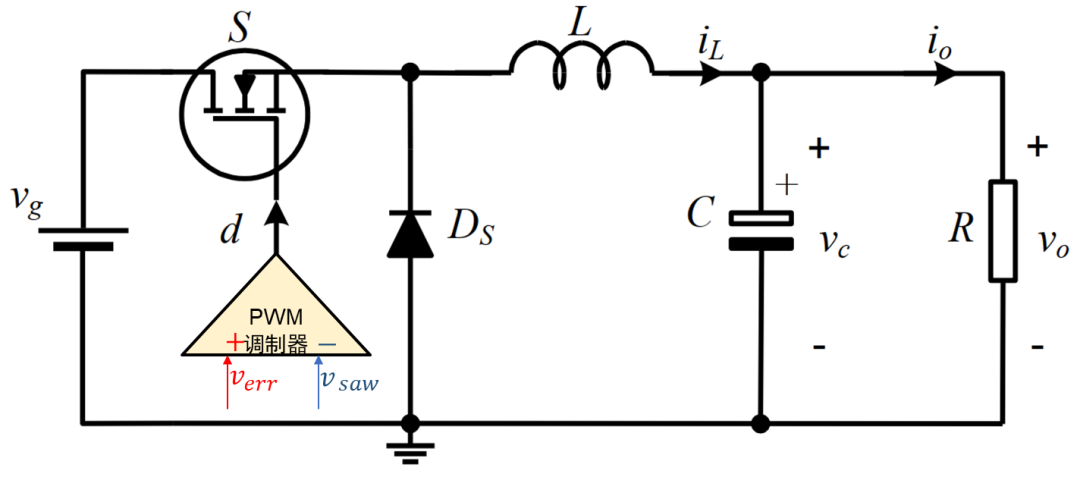
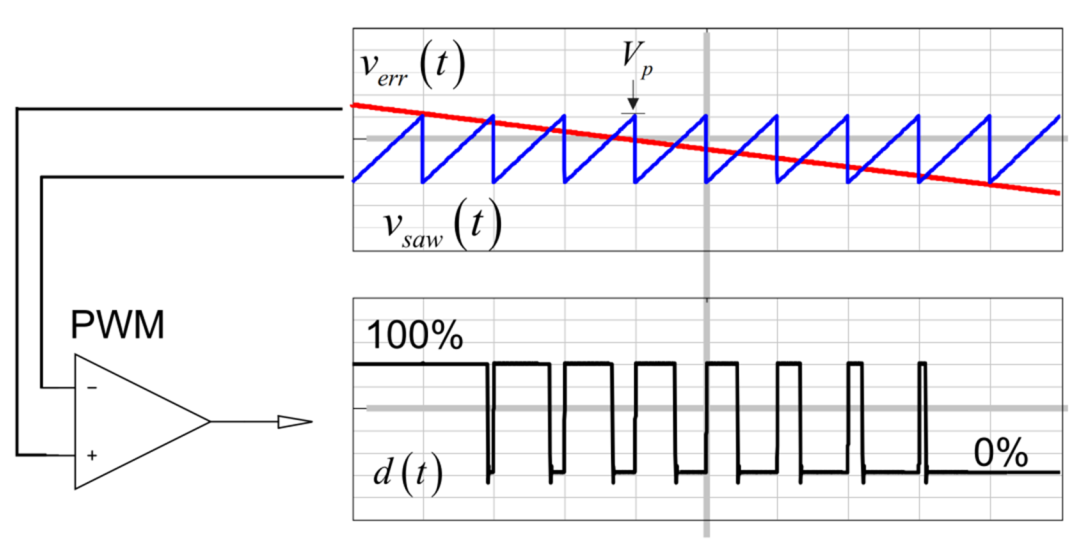
当调制波verr缓慢变化(频率较低)时,PWM调制器被建模为一个纯比例环节是完全合理的。 该环节配合主电路的平均模型,结合补偿器,一起组成了传统平均法完整的闭环环路。
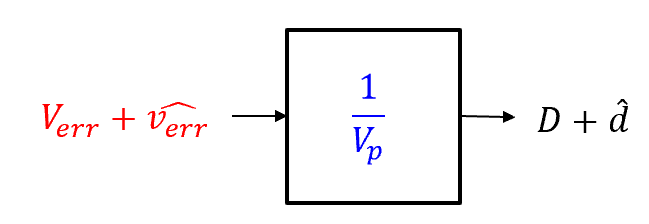
然而,当调制波verr快速变化(频率较高)时,PWM调制器的输出与调制波输入的时刻相关,系统是时变系统,难以用传递函数描述。
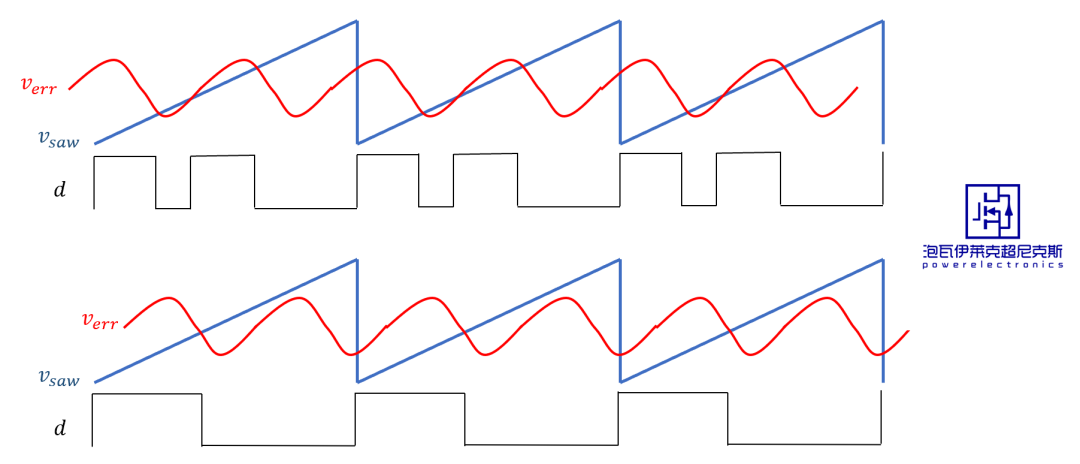
为了方便推导小信号模型,假设调制波verr近似为低频信号,故而PWM调制器和整个系统可当作时不变系统处理,这便是平均模型成立的 “时不变”假设 。
需要注意, “时不变”假设是闭环环路进一步限制传统平均模型的有效频率范围的核心因素 ,相比非线性的开关网络,它会在更低的频率处体现出平均模型的失准。
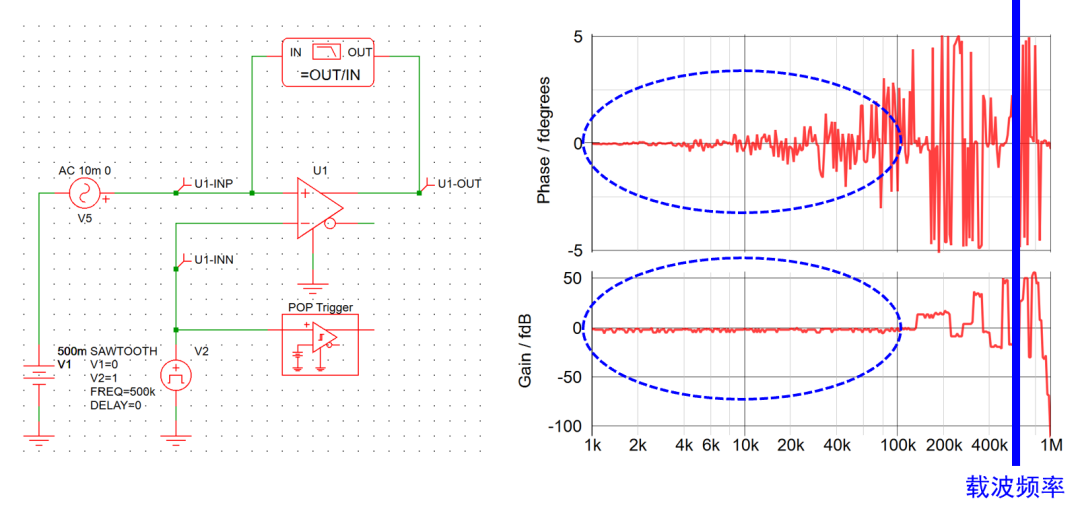
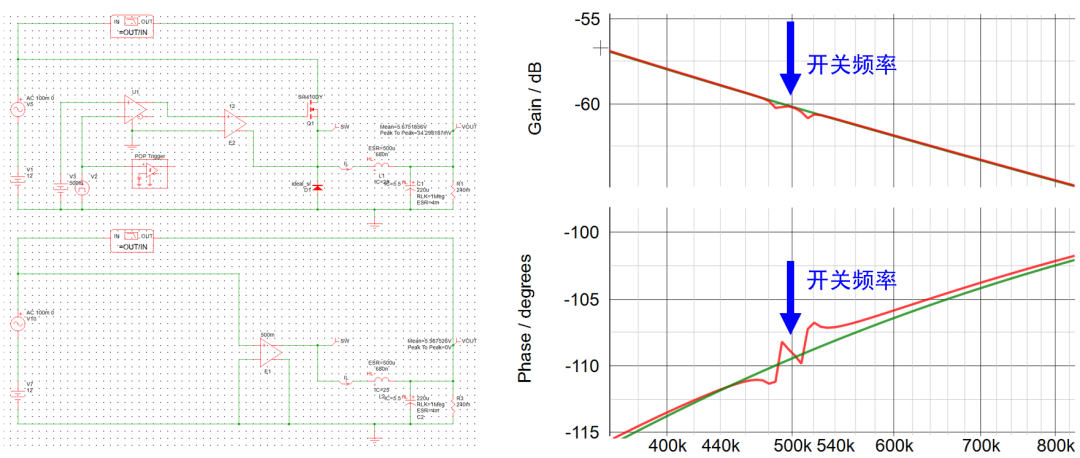
由此回答 问题3 ,当实测频率特性时,注入的扰动输入频率较高时,PWM调制器的时变特性会导致依据传统平均模型求得的小信号模型,在fsw以内并不高的频率处开始,Phase曲线和实际相比已经失准,导致环路的设计只能被限制在相对低频的位置。
因此,使用传统平均模型指导环路设计时,穿越频率一般被限制在开关频率的约1/10~1/5处。 另一方面,实际的开关变换器系统环路很多是类二阶系统,这个位置的带宽设计也是帮助实现充足相位裕量的权衡之举。
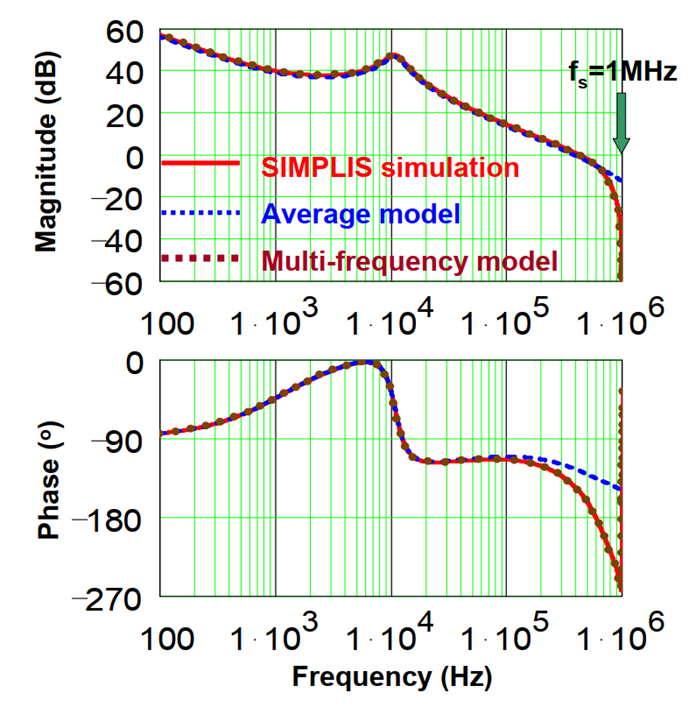
若找到适用于时变系统的建模方法,最后的小信号模型便可解除低频有效的限制,如上图中的“多频率模型”。
同样的,如果能找到突破“低频”,“小纹波”,“小信号”三个假设的其他建模方法,自然可以提高建模的精确度。 下一节将将要介绍这些多样的建模方法。
解析法建模的分类和举例
除了适用于计算机仿真的数值计算建模手法,回答问题4,从理论角度通过解析法建模主要有以下手段。
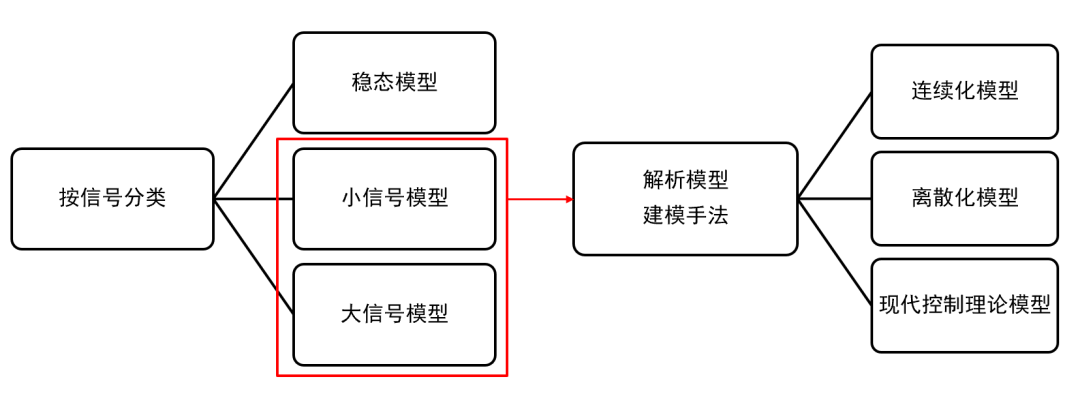
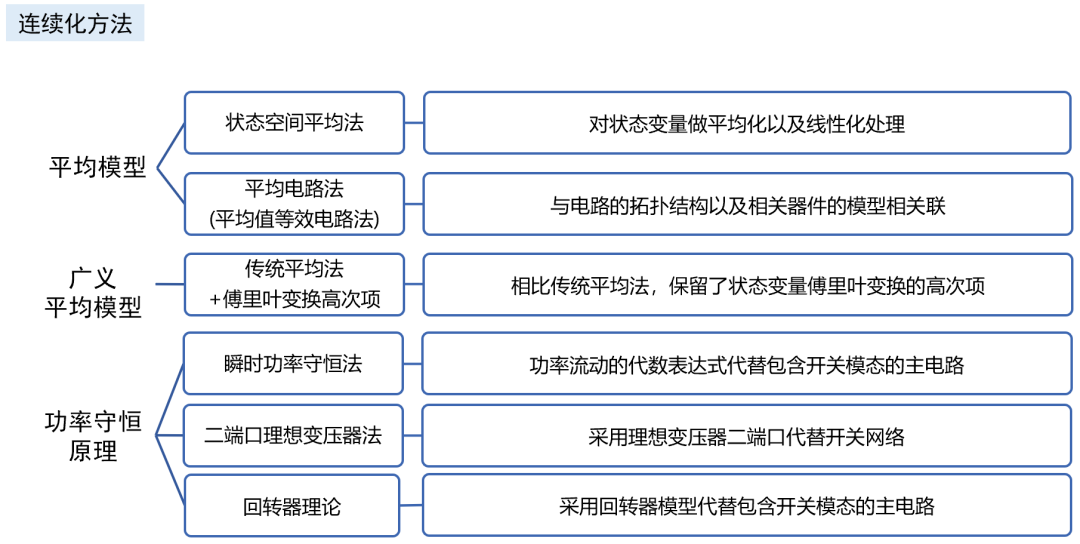
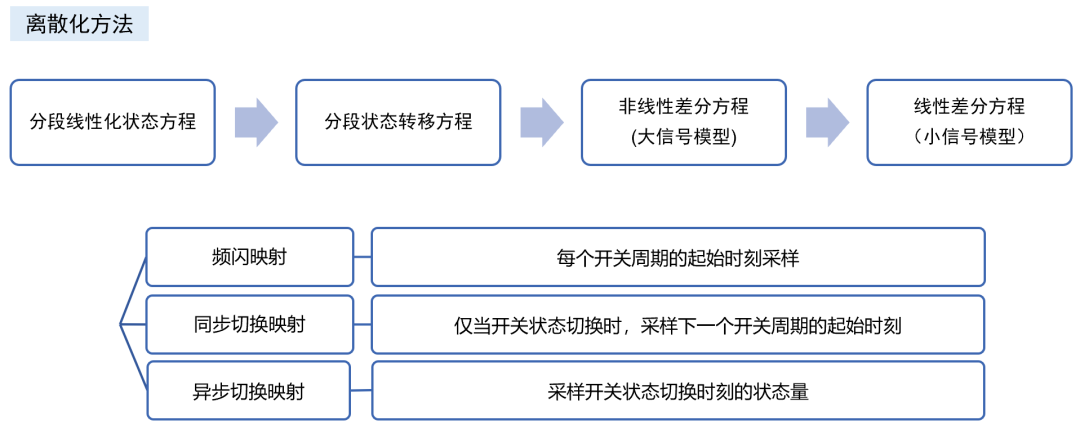
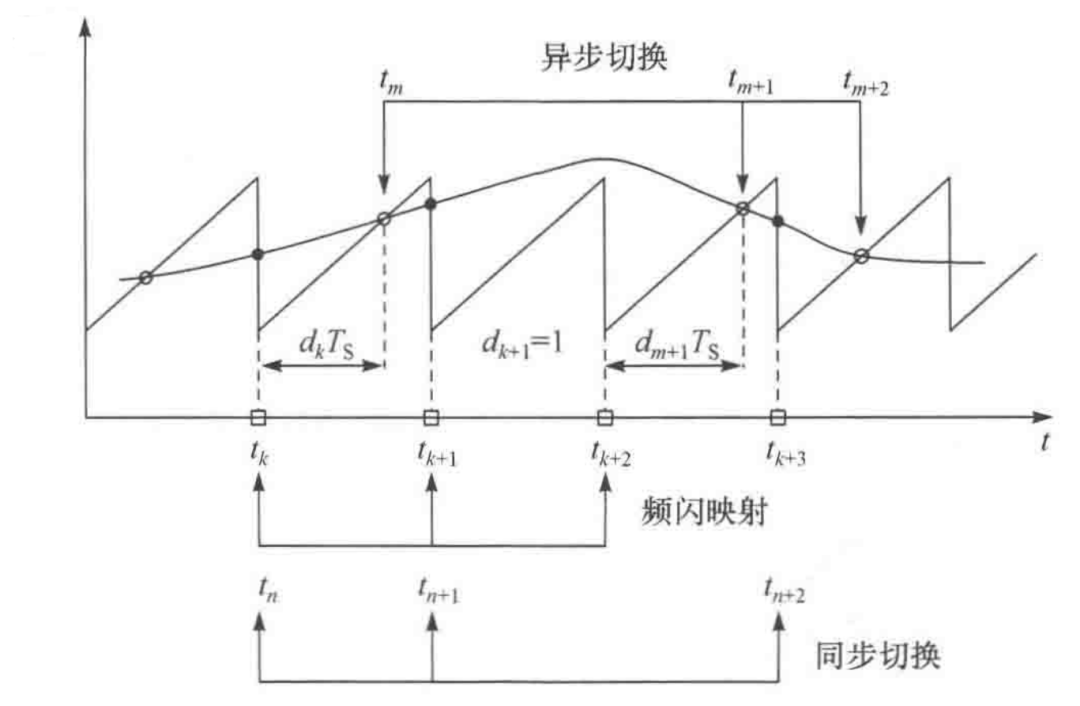
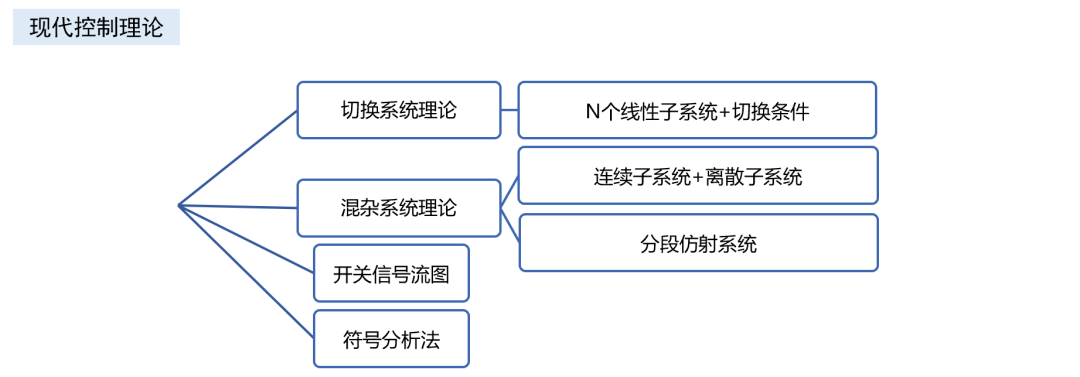
除了最经典的开关平均模型,最常见的应当是离散采样迭代模型 ,离散模型遵循了PWM调制器作为采样保持器的本质,不必拘泥于满足平均模型的“低频”“小纹波”“小信号”等所有假设,能 求解精准的大信号非线性动力学行为模型 ,并还原出1/2*fsw频率处的小信号模型。 它和平均模型的转换关系如下。
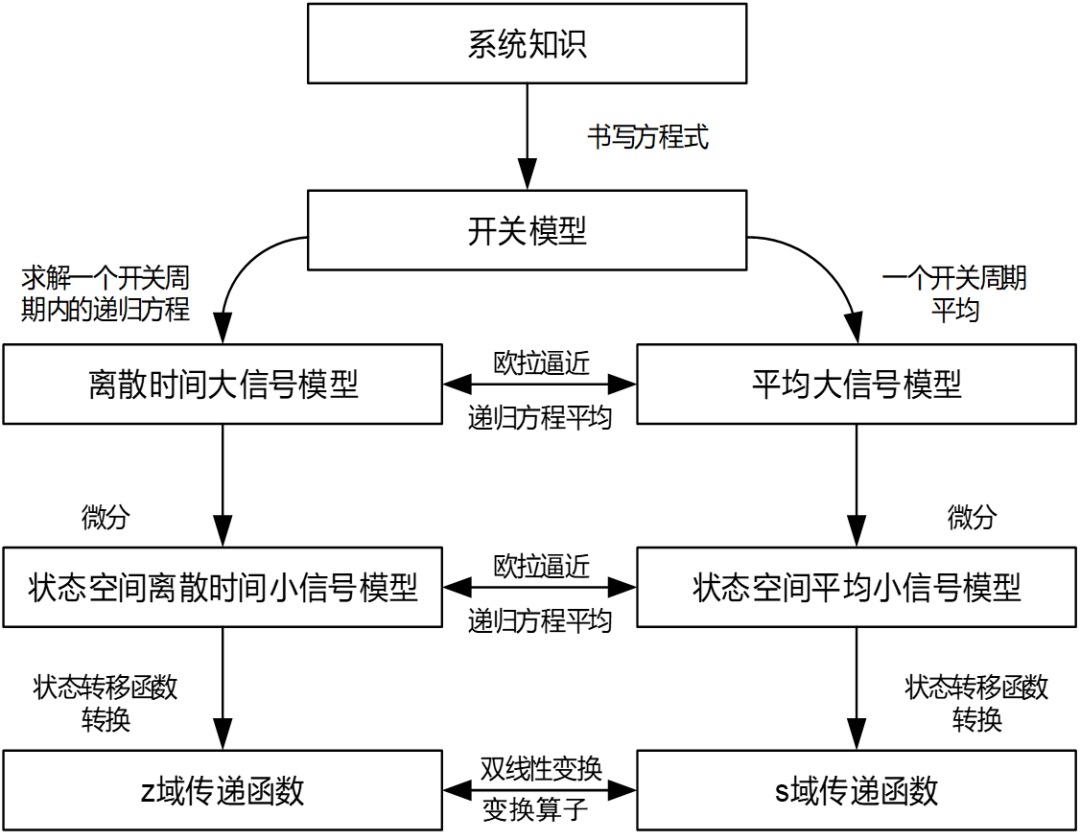
建模方法的发展历史
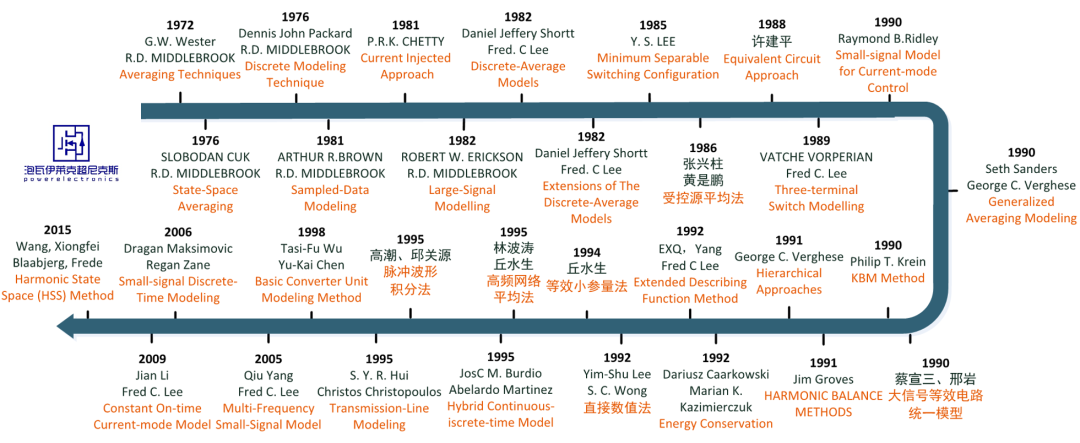
选取部分被引量较高的、有代表性的建模方法,按时间线罗列如下。
选取具有较强主观性,仅供参考,如有遗漏还请包涵
大信号稳定性和小信号稳定性
既然我们可以借助离散模型,建立精准的动力学行为模型,利用非线性系统的分析手段,势必可以发现开关变换器更多的动态运行规律。
和线性系统的稳定性定义不同,非线性系统存在多个平衡态(包含平衡点或周期平衡态),其 稳定性一般指平衡态的局部稳定性 (可进一步明确局部的范围有多大),可用如下方法判断:
- 平衡点:李雅普诺夫Lyapunov稳定性
- 周期平衡态:庞加莱Poincare稳定性
回答 问题5 , DC-DC开关变换器,其非线性的大信号模型,平衡点的局部稳定性,类似于稳态工作点,线性化后小信号模型的稳定性,区别在于 非线性的大信号可以借助李雅普诺夫函数的构造进一步明确局部的范围大小,而不仅仅是小信号模型中模糊的"附近"。
非线性系统的大信号 失去平衡态后,其动力学行为可用分岔与混沌理论进行解释和预测 ,典型的分岔行为有:
- 霍普夫hoph分岔,不期望的周期平衡态,也就是“极限环”低频振荡
- 倍周期分岔,也就是次谐波振荡
如下给出了发生低频振荡,和次谐波振荡的波形实例。
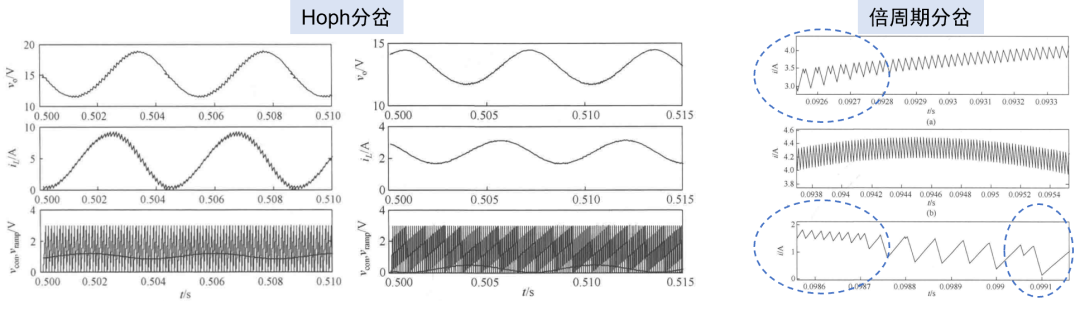
在失稳之前直到临界稳定状态,小信号模型依然有效,可以预测临界稳定的条件。
在失稳之后,意味着不能稳定在该稳态工作点,小信号模型失效,在大信号上可能表现为低频振荡(霍普夫hoph分岔)或次谐波振荡(倍周期分岔),以及其他更复杂的动力学行为。
通过对小信号模型临界稳定的具体特征进行识别,可以在一定程度上预测失稳以后的行为。 但其充要条件必须严格来自于分岔与混沌理论的推导,极少文献对此进行严格证明。
- 如下为小信号波特图,预测Buck电压模式控制中,低频振荡(霍普夫hoph分岔)临界条件(Kp足够大)的实例。
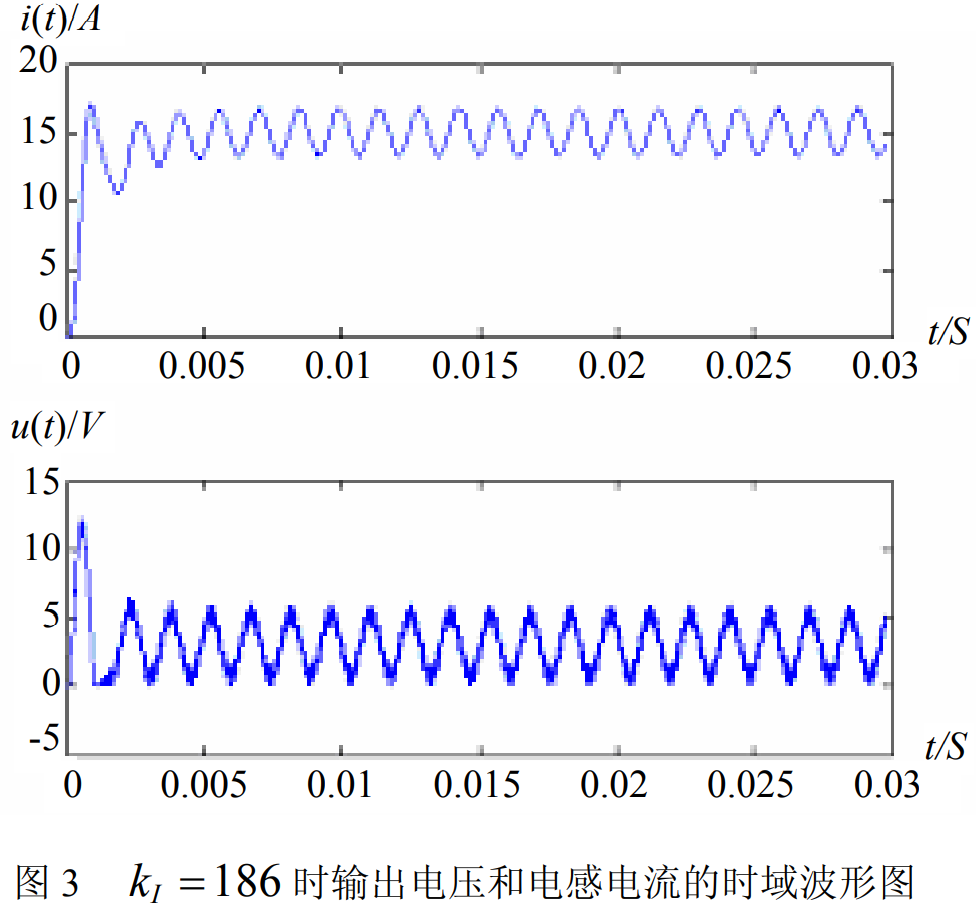
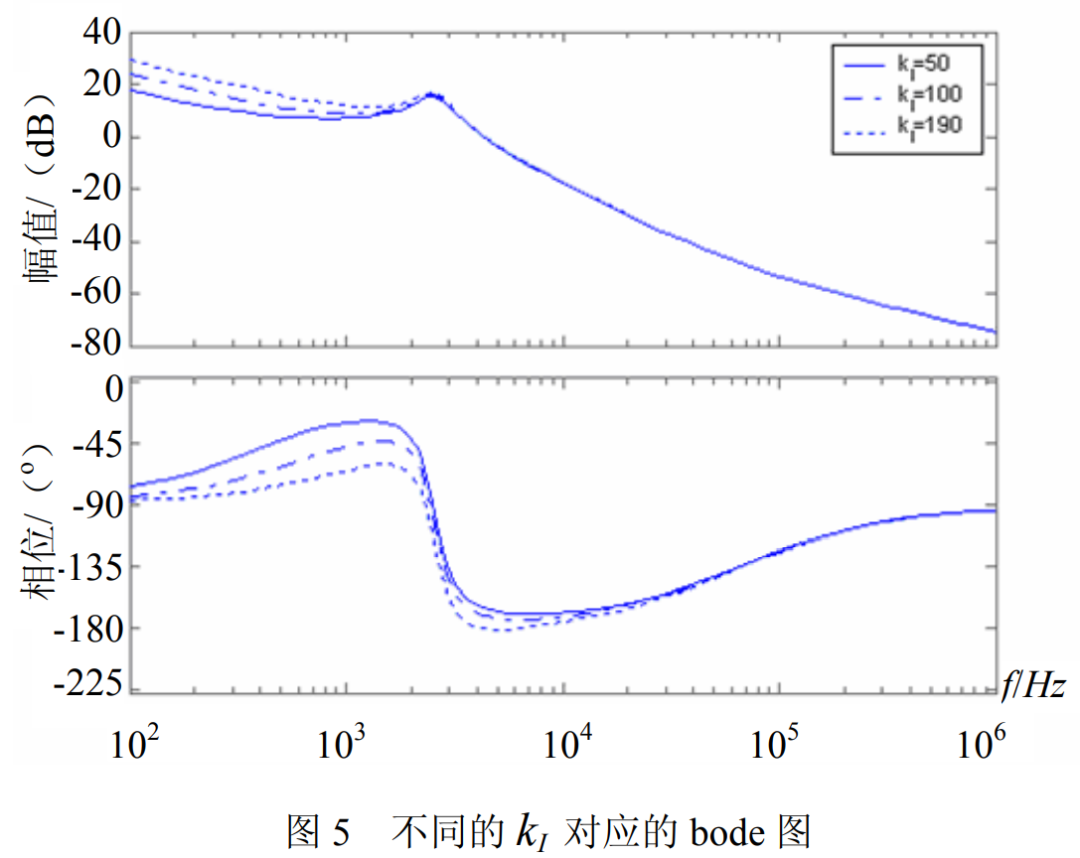
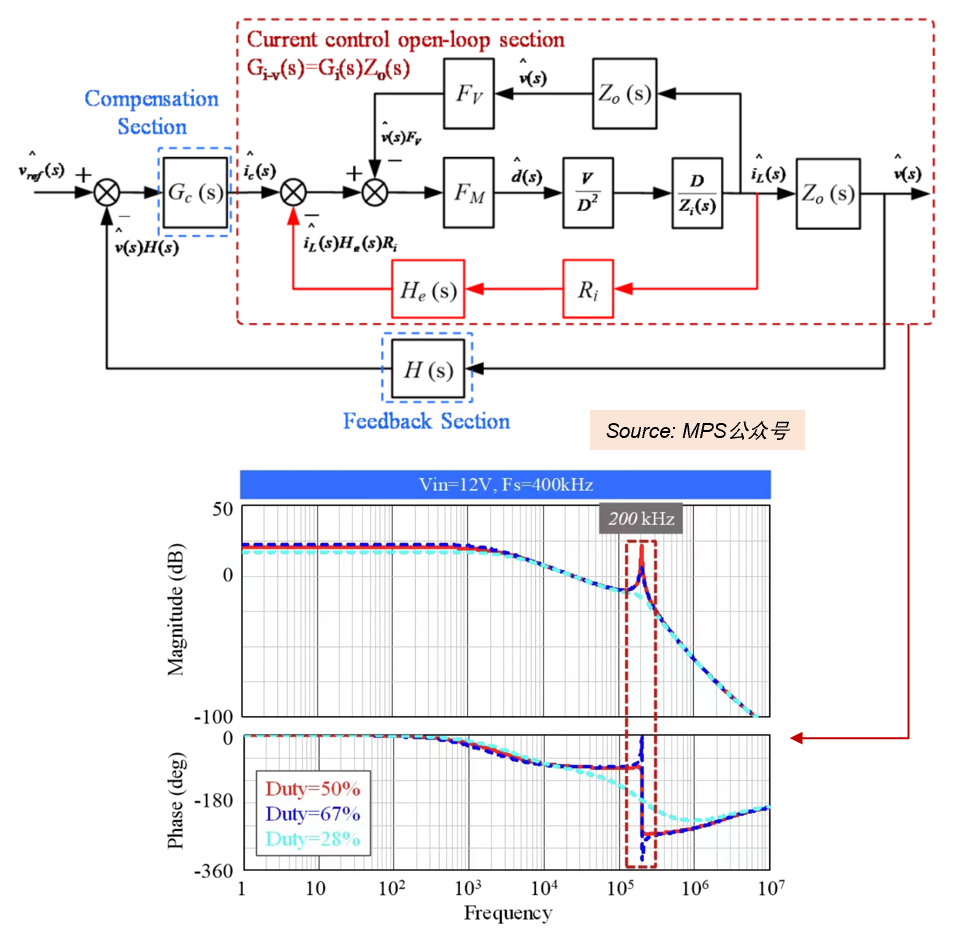
- 如下为小信号波特图,预测Buck峰值电流控制中,次谐波振荡(倍周期分岔)临界条件(D=0.5)的实例。
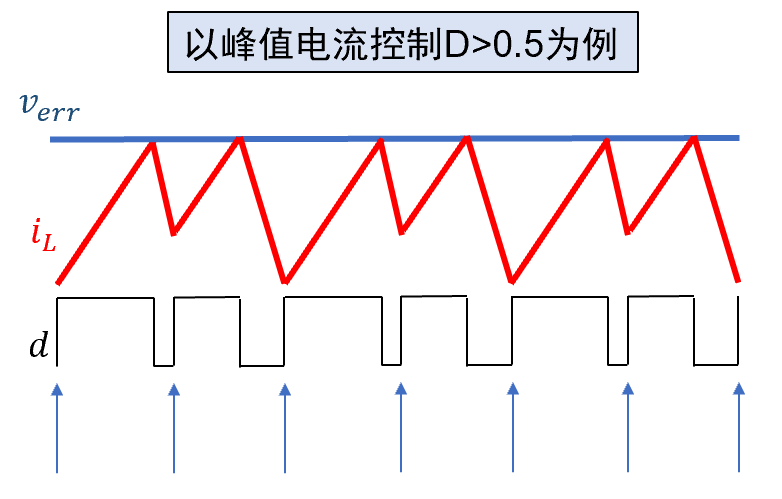
-
误差放大器的大小信号环路2023-03-17 5465
-
BUCK变换器设计2021-11-16 1706
-
Buck变换器的工作原理与设计的学习课件免费下载2020-12-07 1485
-
buck级联推挽变换器小信号建模的问题2020-11-17 4023
-
谐振变换器到底是什么及理想和非理想buck变换器的模型介绍2020-11-07 11576
-
buck变换器介绍_buck变换器设计2018-01-10 9457
-
Buck变换器的CCM等效电源平均电路模型2017-12-19 1952
-
DCM_Buck_Boost变换器的建模与控制设计讲解2016-01-04 1730
-
【分享】Buck变换器的设计与仿真2015-05-25 11057
-
BUCK变换器2012-08-14 4107
-
Buck变换器参数辨识的分析2009-06-30 1771
全部0条评论

快来发表一下你的评论吧 !

