开关电源学习笔记

观察点

为了仿真变换器加上补偿网络后的传递函数，可以直接把环路在误差电压处断开，以占空比信号为输入，误差电压为输出，进行交流分析。 所谓的断开，其实可以与之前一样，接入一个大电感和大电容即可。

 

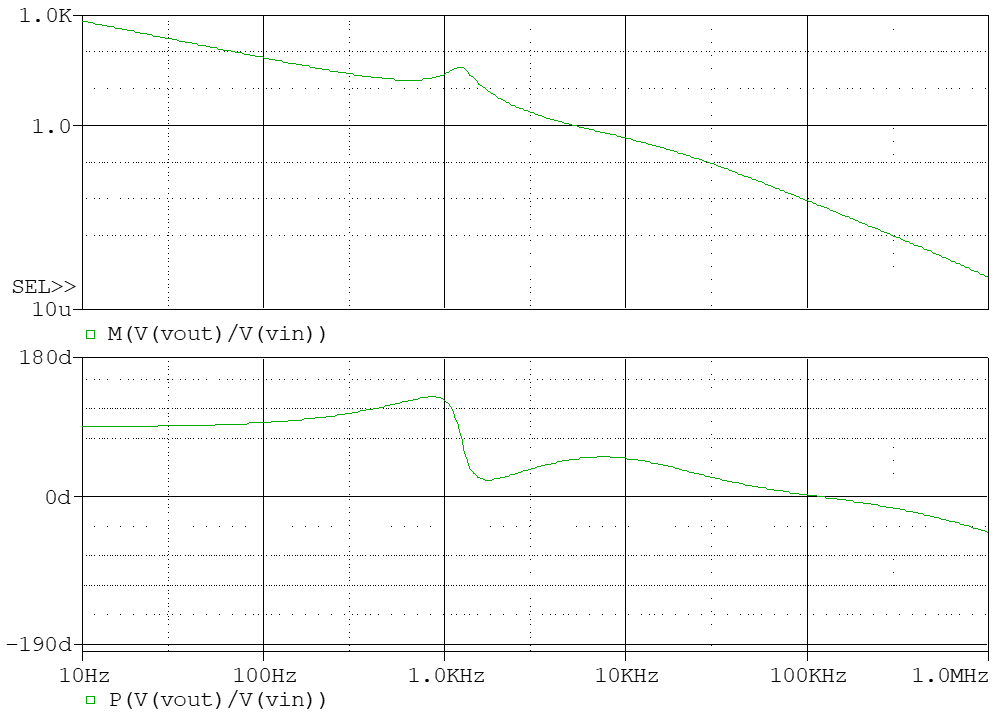
注意这里忽略了放大器引入的相移，因此相位从正的开始，相位裕度以与0°线的距离计算。 可见补偿后的系统相位裕度抬高了。

频域参数

当输出信号和控制信号之间的相位差减少为0°，则变成正反馈振荡器。

交叉频率处的输出容抗可以近似表示闭环输出阻抗，所以可以近似计算出输出瞬态阶跃电流作用下的输出电压脉冲

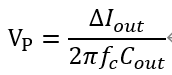
根据这个式子以及稳态纹波需求，可以确定交叉频率的取值。 不过对于有RHPZ的拓扑，一般就直接选定为RHPZ所在频点的30%，同时又应该保证交叉频率在LC谐振频率的5倍以上，给设计带来困扰。 对于没有RHPZ的拓扑，可以直接设定为开关频率的20%以下。 脉冲峰值固然与上式有关，不过恢复时间则由相位裕度决定。

构建补偿网络

构造零极点的知识均已知晓。 值得一提的有构造RHPZ的方法，就是将原输入信号与高通滤波器后的信号相减

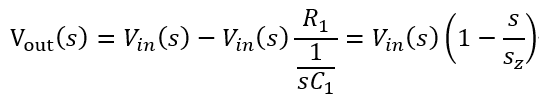
零点频率即RC分之一。

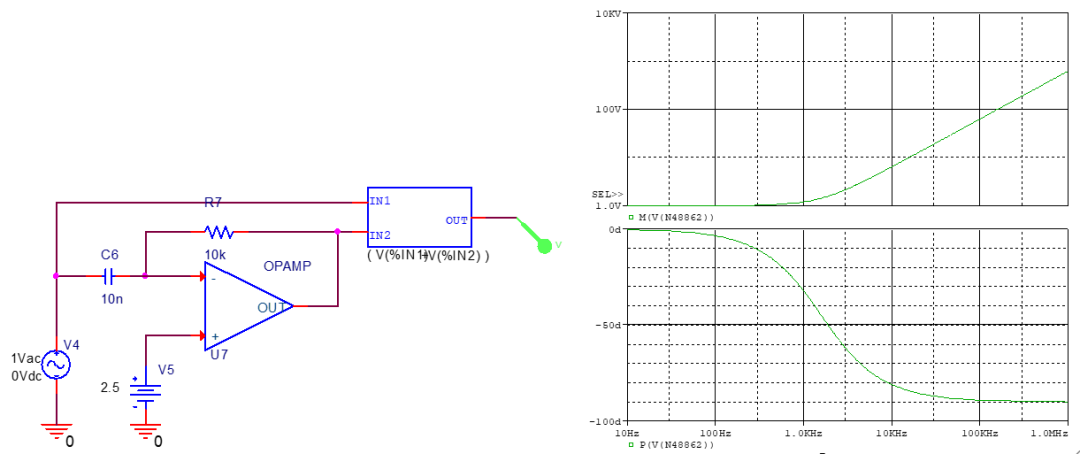
RHPZ是变换器间接能量传输的结果。 在CCM的Boost变换器中表现为，如果负载出现向上的阶跃，造成占空比信号变大，即减小，即电感向负载供电流的周期减小。 但是电感电流不会马上增大，而是以固定步长增加，这个过程中输出电流可能会反而比原来更小，这就是RHPZ的影响。 如果系统响应很快，那么在负载跃变瞬间，反馈环的占空比输出会因为输出电压的反向减小而迅速增大到1，使变换器无法工作，这也是Boost变换器环路设计要降低交越频率的原因。 一般选择在最低RHPZ的1/3处。 DCM时变换器仍存在RHPZ，但其被推到高频处，因此环路设计的困难相应降低。

各个频率响应对应的有源电路网络依次示下：

积分器

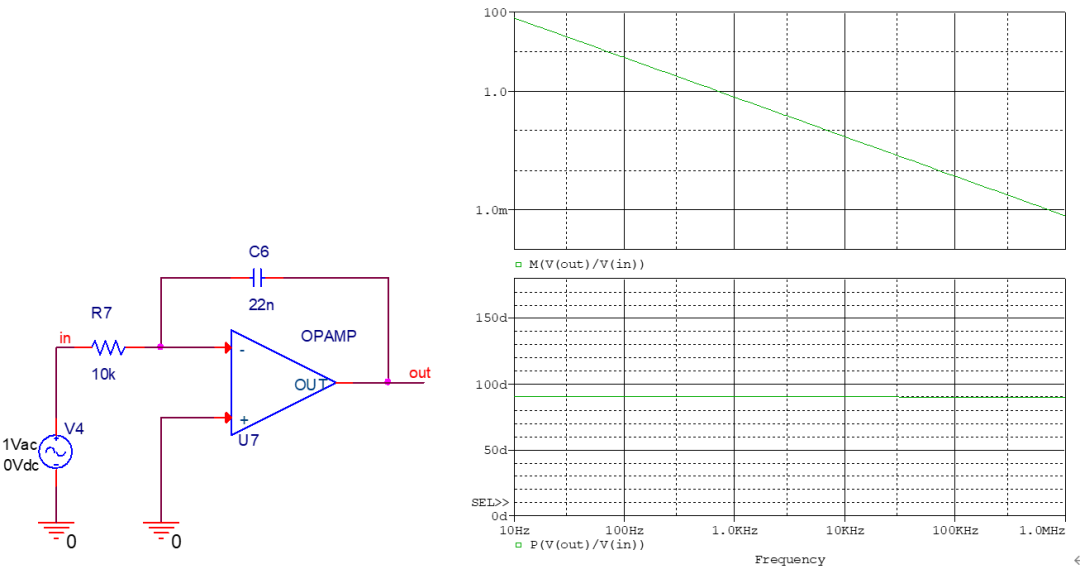
零极点

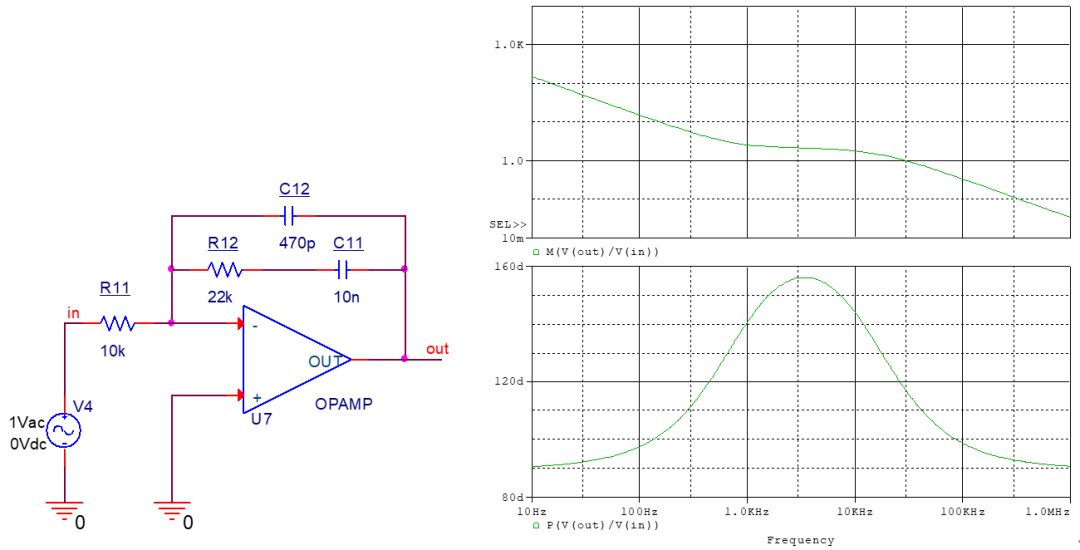
极点位置为

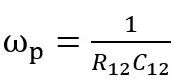
，零点位置为

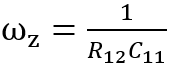
，并且有积分器的效果。 这种补偿网络的特点是中频部分存在一个固定增益区，并且该区域的相位具有超前性质，相位的最大值出现在频率为

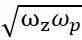
处。 用于电流模式和DCM。

零极点对a

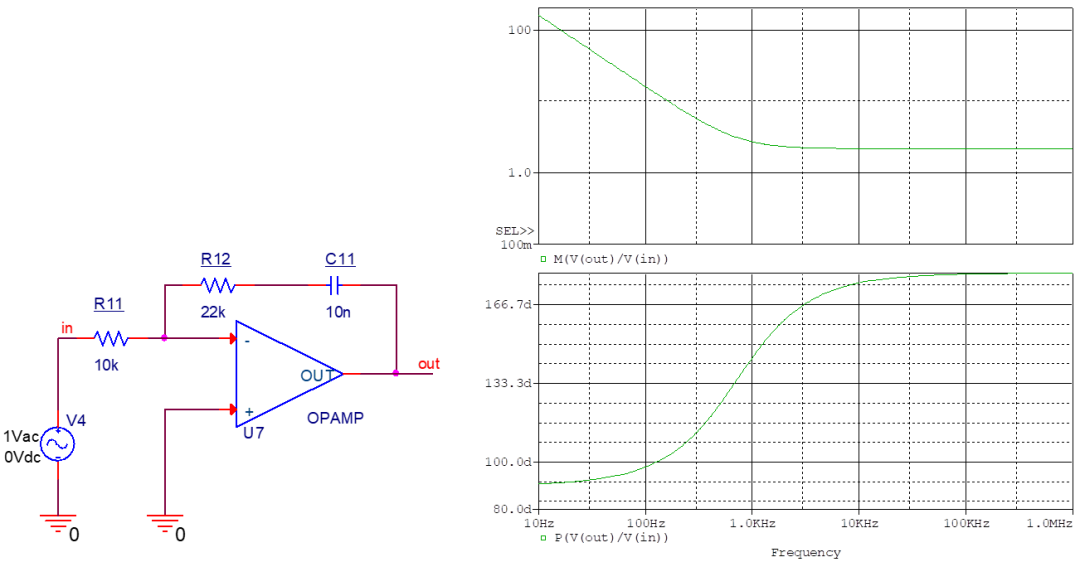
这是上面的特殊情况，即C12为0时，极点被排除，因此不存在高频段的增益下降，相位也一直接近同相。 在无需考虑ESR零点的场合可以用这个简化的补偿器。

零极点对b

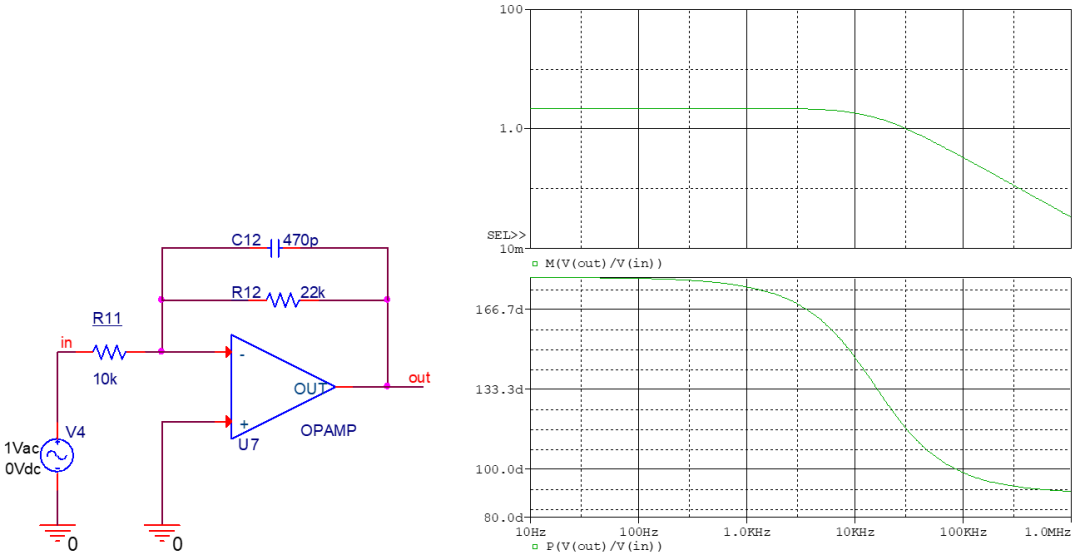
这也是上面的特殊情况，令C11为无穷大，则变成一个原点处的零点，相当于与积分器的效果相抵消，因此低频至中频都为固定增益。 明显的缺点是直流增益太低，稳态精度无法保证。

两个零极点对

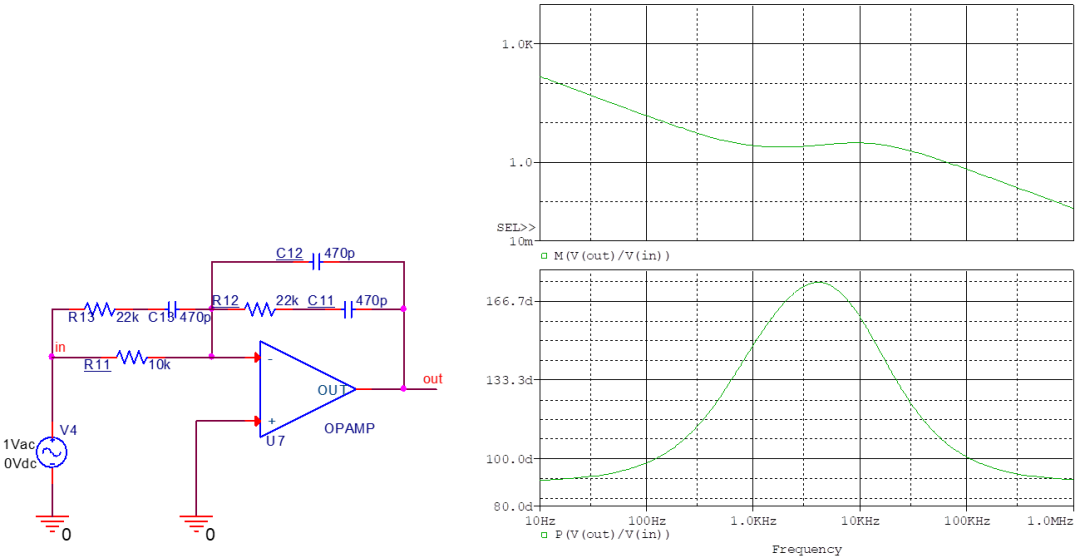
传递函数为

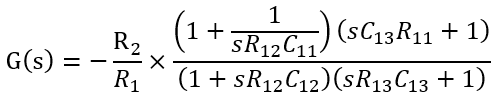
式中就可以看出零极点位置和直流增益。 比起单个的零极点对，两个零极点对提供了更大的直流增益和更大的超前相角，因此是最完备的一种补偿网络。

注意，实际的运算放大器必定自身附带一个低频的极点，其本身的增益就随频率的增大而减小，所以实际设计时还需要根据具体的运放进行参数设计。

K因子

一种从变换器开环特性得到k因子等参数值后，直接推导各类型补偿网络组件参数的方法。

首先看各类型补偿网络需要考虑的补偿参数。

积分器：极点在原点处，所以它只能通过平移增益曲线，改变系统的交叉频率，并引入一个90°的相移。

零极点对：除了具有积分器的平移曲线的效果外，还引入了一个超前相位，某点引入的相位增加量计算为

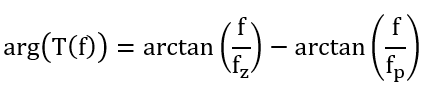
因此在交叉频率处，用k因子的方法可以令极点频率为kf，零点频率为k分之一f，则相位增加量

解出

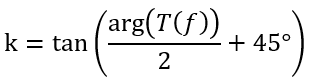
根据所需要的相位裕度和变换器本身的相移，加上积分器引入的90°相移来确定

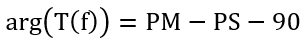
书中给出了不同k值下该补偿器的响应，k=1时退化为积分器，随着k增大，零极点距离增大，超前的相位增大，而直流增益减小。

双零极点对：与上面相似，这里假设双零点重叠，双极点也重叠，那么令极点频率为倍的f，则

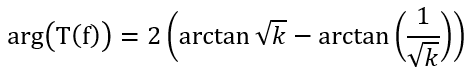
解出

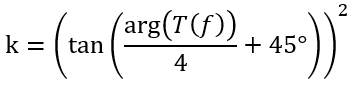
接下来的式子和关系与上述一致。

K因子设计步骤

1、获得变换器交流响应。

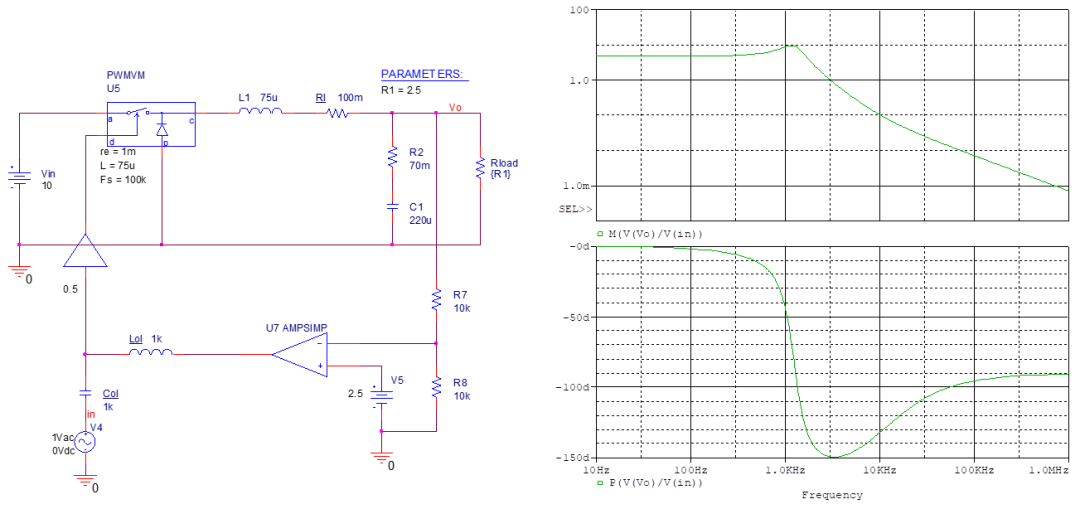
用游标看出交叉频率为3kHz，相移149°。

2、选择交叉频率和裕度。

开关频率为100kHz，而LC峰值频率为

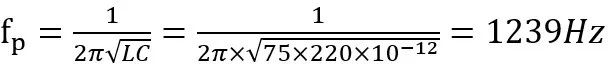
如前所述应该选取6k以上的交叉频率，但是书中选取了5k，先按书中选取，后面再观察不同。

若选取5k，先观察变换器响应中5k处的数据，得到相移为-146°，增益为-9.2dB，期望的相位裕度为45°。

3、选择补偿器类型。

可见到变换器的响应相位滞后达到180°，稳妥起见可以选择双零极点对补偿器，最高可以补偿180°超前相位。

4、应用公式计算组件。

运用上页的公式，计算出k因子和元件参数

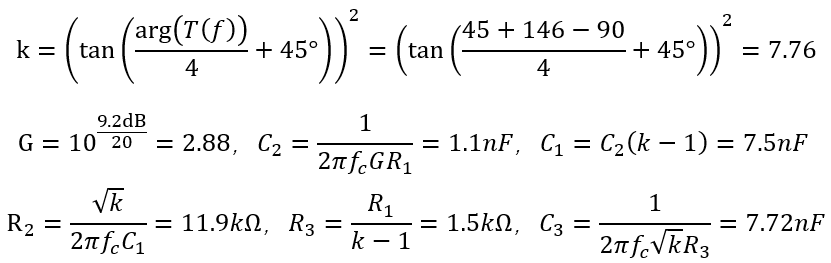
顺便可以计算出补偿器提供的零点和极点频率分别为1.8k和14k。

5、连接补偿器后开环扫描。

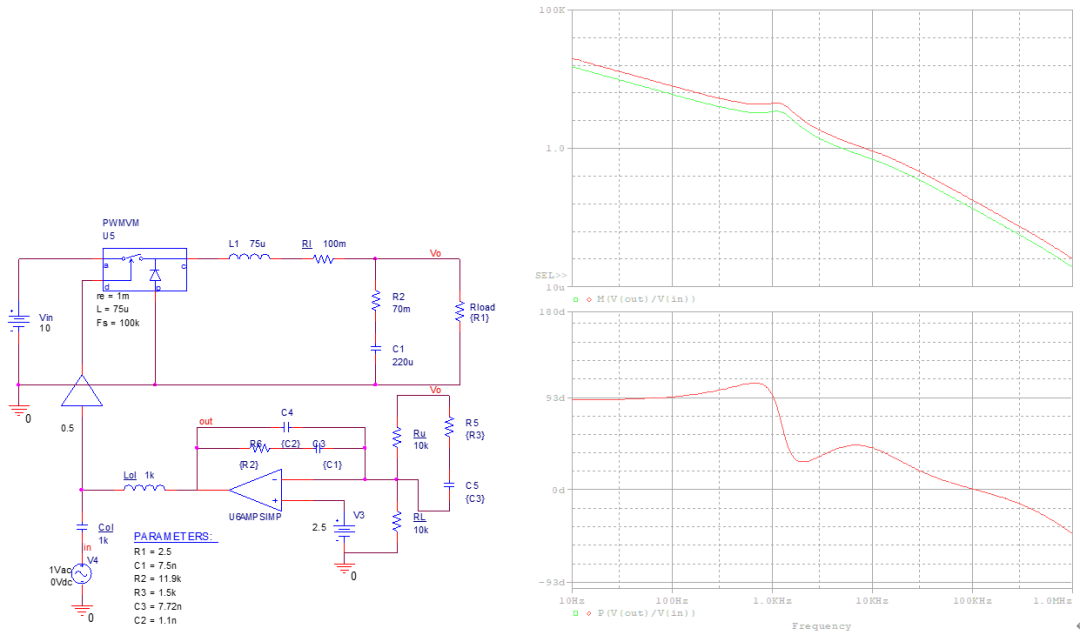
标准输入并带满载情况下的开环响应，交叉频率为5kHz，相位裕度为43°。 变化输入电压为20V，即图中红线所示，环路增益增加了1倍，即曲线被抬高了3dB，因此交叉频率变为8.45kHz，相位裕度为44°。

6、变化ESR和负载检查相位裕度。

以上测得是负载电阻为2.5Ω即电流为2A时的响应，若增大电阻至进入DCM模式，观察补偿器的功能是否受影响。 下图看出，因为变换器在低频处退化为一阶系统，低频段增益减小，所以交叉频率明显降低，分别为613Hz和1kHz，相位裕度分别为39.5°和59.5°，在不同输入电压下的相位裕度相差更大了，即对输入电压更加敏感。

如果变化电容的ESR，道理相同，负载恢复满载情况，若取值变为200m时如下图，交叉频率变为7.83kHz和15.56kHz，相位裕度变为74°和55°。 可见ESR的增大会使得其零点提前出现，使得交叉频率后移，并且提高中频段的相位。

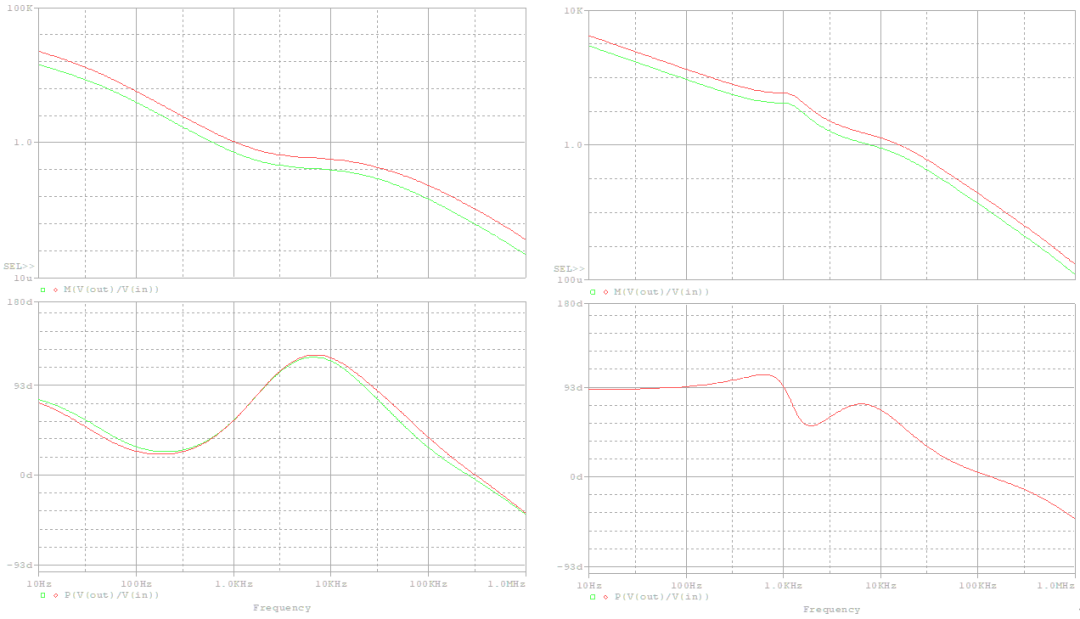
负载为50Ω时 ESR为200m时

7、观察瞬态响应。

前面给出了一个近似估计电流上升阶跃下，电压响应尖峰的计算式

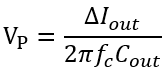
如果作0.1A到2A的阶跃，大致算出峰值为

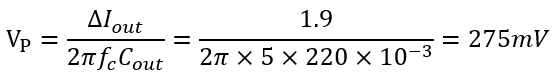
即从5V下降到4.725V。 搭建仿真模型，用ABM+脉冲信号源实现负载切换，结果如下

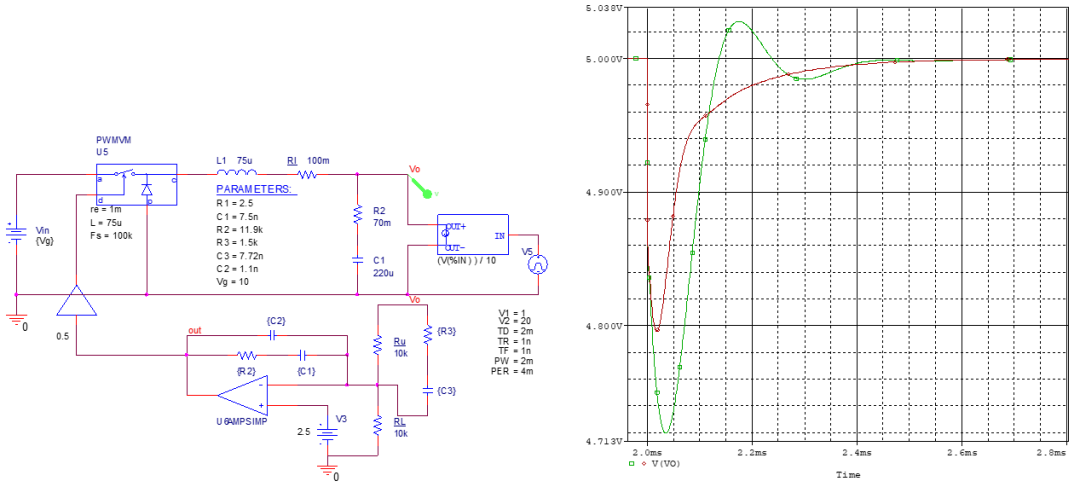
电压跌落为4.713V，与计算值近似相等，误差可能来自ESR等。 书中给出该式，只说明用来计算欠脉冲，若用来计算电流下降阶跃下的电压超调，则似乎不符合仿真结果的5.24V。

下图给出了全貌，明显，DCM下到CCM的切换很快，建立时间大约0.4ms，而DCM切换到CCM则很慢，需要大约5ms。

图中同样以红线示出了20V输入电压下的瞬态响应，说明Buck变换器中确实是以最低输入电压为最恶劣条件，而高输入电压下具有更好的动态性能。

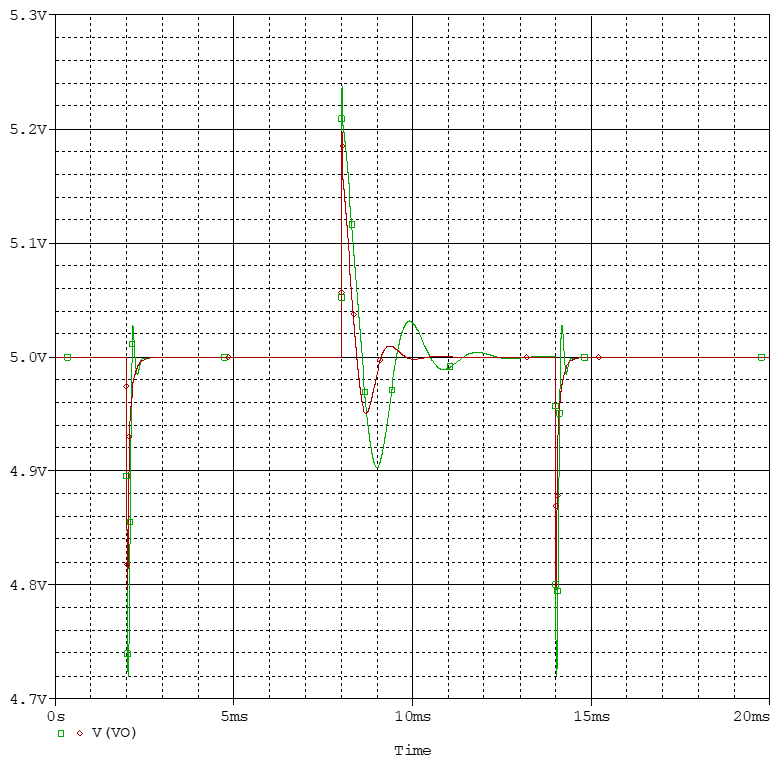
除了输出电压响应外，还应观察误差电压的瞬态响应，这才是变换器在控制意义上的输出。

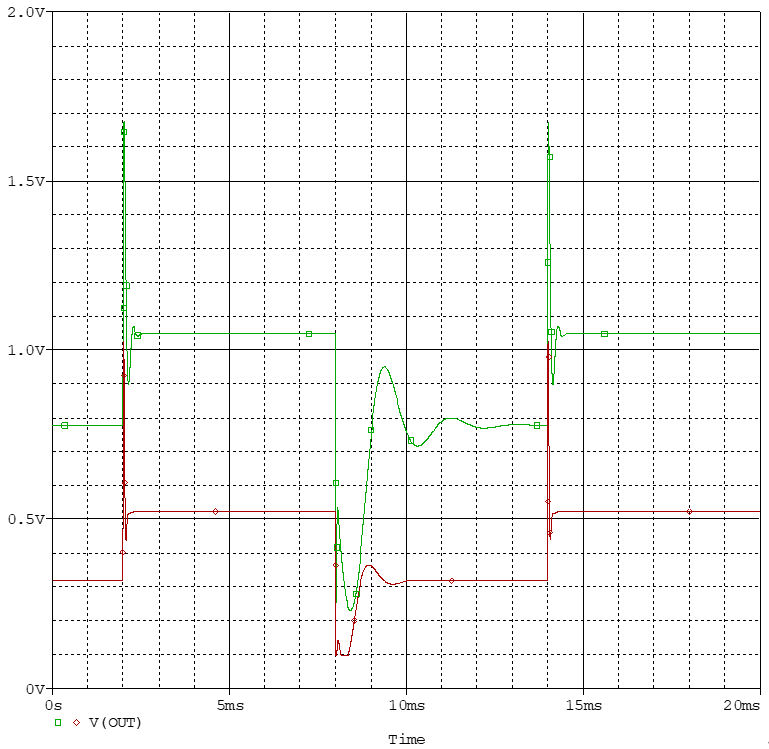
书中到后面也说明了当交叉频率为8kHz时，响应峰值降低为171mV，系统性能应是有所改善。 重复上述步骤，8k处的曲线数据为相移137°，增益-16.5dB，同样选择45°裕度，双零极点对补偿器，列式如下。

 

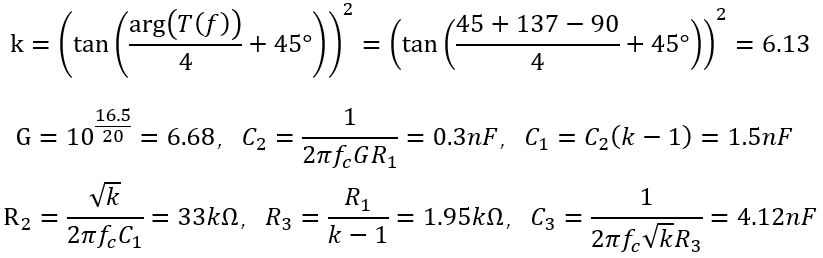
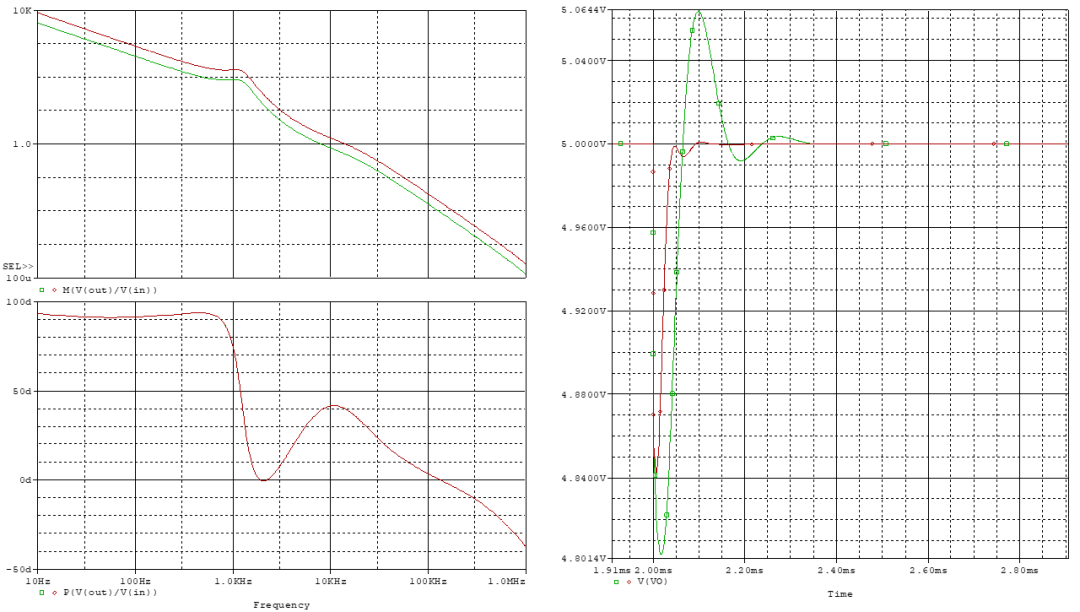
得到曲线如上，与前述相同，用输入电压分别为10V和20V时进行对比，10V时，交叉频率为7.98kHz，相位裕度为42°。 再观察瞬态响应，理论计算的峰值应为，图中为4.8V左右，相差不大，说明该估计式具有足够的精确度。 仔细观察上图中的相位曲线，可以看出一些问题。

K因子法的缺陷

该方法虽然简单，它对响应曲线形状忽略不计，即忽略了可能存在的谐振峰，而只考虑交叉频率。 这样有可能在交叉频率之前出现相位裕度减小到0的情况，如上图所示。 在交叉频率较高为8k时，出现了相位降低到0，增益仍为10以上的情况，这样在该频点很容易就有振荡现象，称为条件稳定。 这种问题出现的原因是K因子法在放置零极点时只考虑交叉频率的实现，而并未考虑零点位置与LC极点位置大致重叠这一要求，所以就会出现无法抵消LC极点引起相移的问题。 所以K因子法好虽好，若要妥善设计，还是应该采取一般的零极点放置法进行配置。

这种一般的方法，精确放置了每一个零极点，可以制作专用的计算表格。 书中提供了一种利用仿真软件进行参数计算的图纸，似乎只能用Ispice，Pspice尚不知可否。

用放置零极点的方法，就不会出现条件稳定性的问题了，图如下，相位裕度为36°。 这种方法的缺陷也正是K因子法的优点，即交叉频率无法精确定位； 另外，书中的理论和实验也表明，K因子法放置的零点频率较高，瞬态响应也会快于放置零极点的方法。 所以各存利弊。

电流模式补偿网络

以上讨论的内容均针对二阶的电压模式Buck电路。 对于电流模式控制来说，变换器的模型在低频呈现为一阶系统。

回顾一下电流模式控制的相关设置。 为避免次谐波振荡，需要加入斜坡补偿，在输入电压为10V时，电路中电感电流的上升和下降斜率一样都为66mA/μs，补偿斜率可以为其一半。 若采集电阻阻值为0.4Ω，则补偿斜坡电压为13.3kV/s。

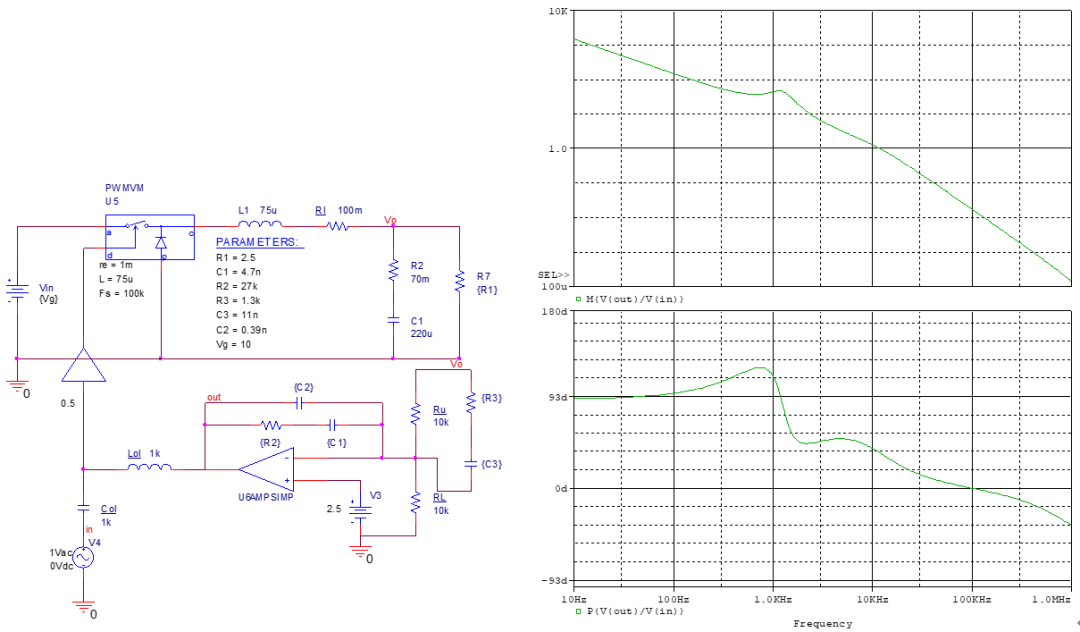
同样运用K因子法，选择交叉频率为10kHz，相位裕度为80°。 先观察开环曲线。

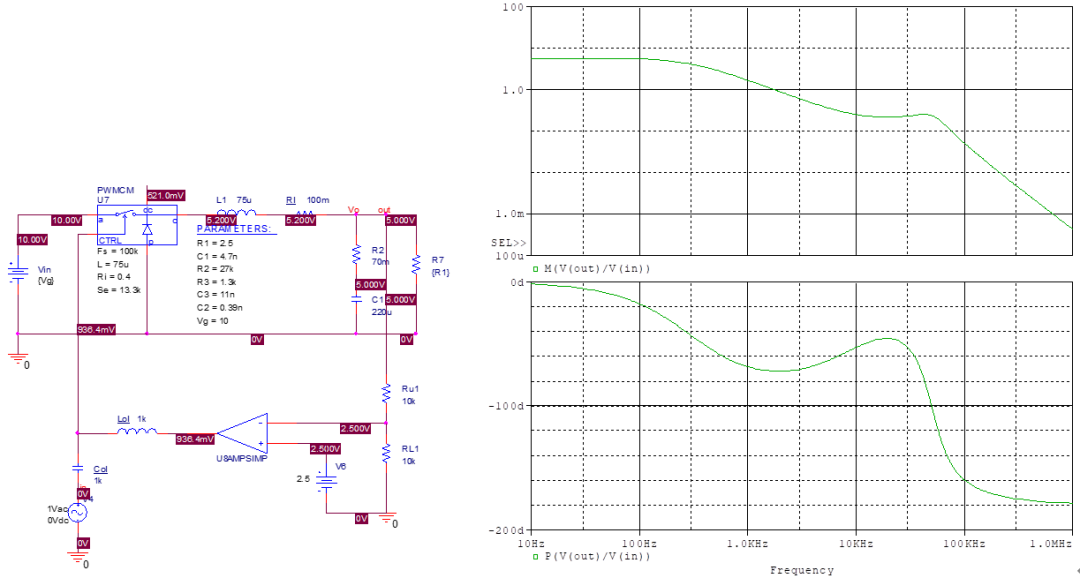
得到10kHz处相位为-52°，增益为0.25=>-12dB。 因为相位滞后在90°以内，可以用零极点对的补偿器（2型）。

计算式如下

 

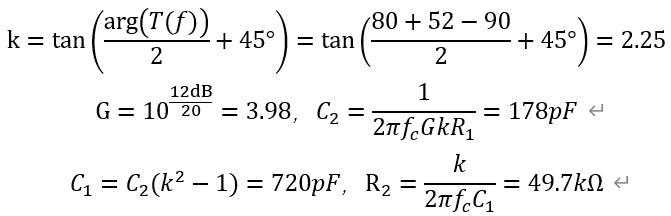
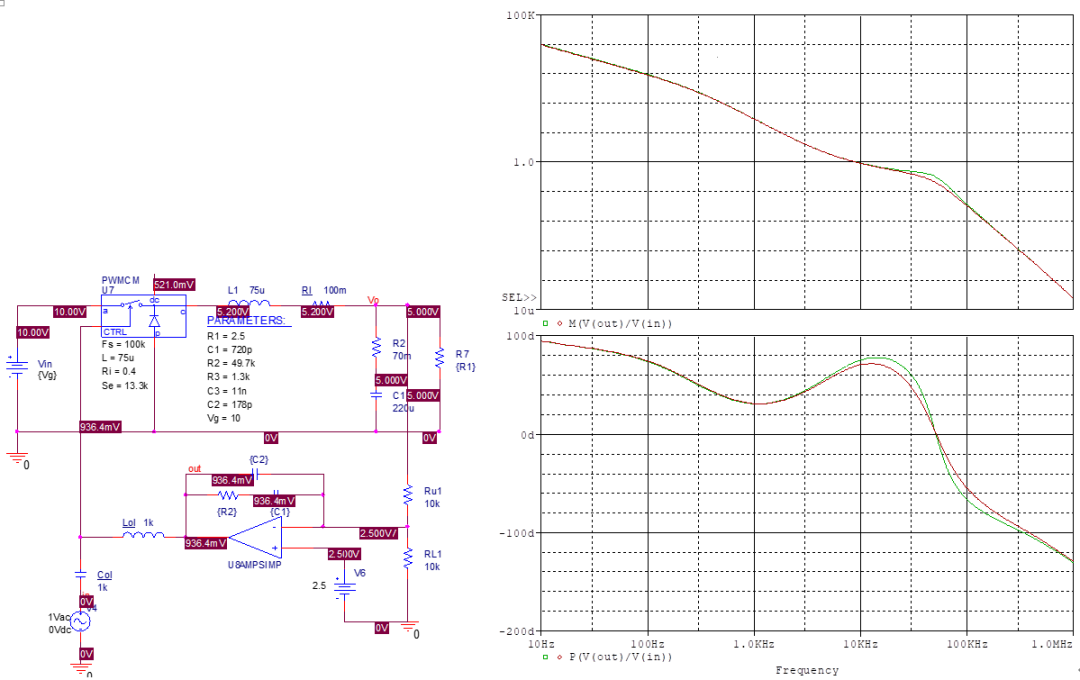
得到补偿后的特性曲线如图。 交叉频率为9.1kHz，相位裕度74°。 值得注意的是在输入电压分别为10V和20V时，两条曲线几乎重合，这是因为电流模式控制下，理论上的音频敏感度就是0，即输入电压的变化不会对系统造成影响。 略去了负载阶跃测试，因为可知道电流模式控制下系统在低频变为一阶系统，自然在阶跃作用下是不会产生振荡的，但峰值电压由输出电容决定，对电压模式和电流模式都是一样的。

此例可以看出K因子法对电流模式的设计还是很有优势的，因为一阶系统的特点，系统本身的相移就不大，所以不会出现条件稳定性的问题。

实际设计之TL431反馈

实际工业应用中已经很少用运算放大器设计补偿电路，而是将其与基准源合二为一，利用TL431内部的集成误差放大器就可以设计出高性能的补偿电路。 TL431的参考电压为2.5V，TLV431为1.24V，且电流更小。

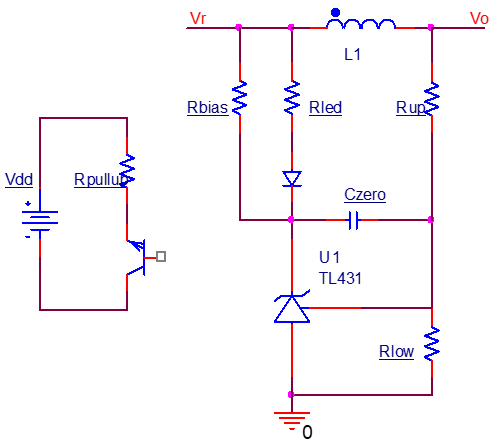
在一般的反馈环路中，连接光耦LED的支路为快支路，分压网络为慢支路，如图所示。 对于小信号的研究，由于TL431的动态电阻与Rled比起来小得多，忽略后由KVL得

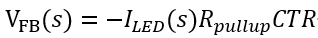
VFB为最终反馈回到芯片FB引脚的电压。

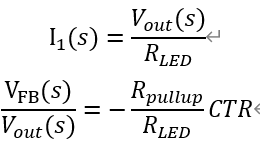
就得到了快通道的传递增益，在高频区难以降低，使放置零点成为一个问题。

整个反馈可以看作快慢通道的叠加，与慢通道叠加后，推导反馈环路的传递函数

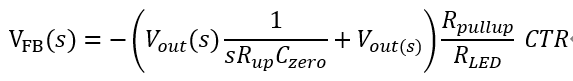
即

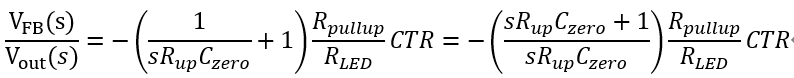
表明了系统中存在原点处极点和一个零点。

必须要明白的一点是，这个电路是实现前面所述补偿网络的方法。 对比零极点对补偿网络，还缺少一个非原点处的极点，可以直接在光耦的输出与地之间接入电容。 得到的零极点位置分别为

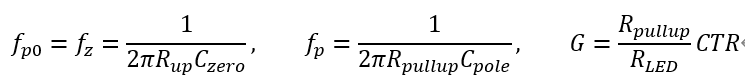
注意到第一条式子的关系，所以曲线的斜率刚好在0dB处发生转折，结果就是中频增益G与零极点位置无关。

下面用TL431实际设计补偿器。

K因子+431

用k因子法直接把零极点放置在

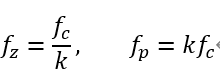
构造零极点对的补偿器做法较为简单，基本上与前述的一般方法一致，直接代入计算即可，得到的响应与前面用运放搭建的结果是一致的。

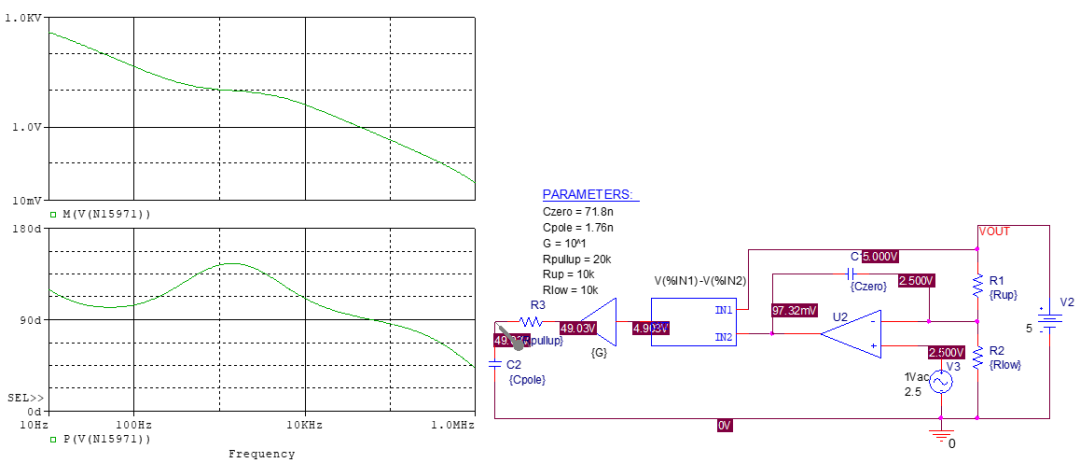
如果搭建双零极点对补偿器，则需要考虑快通道的影响，即高频区存在的增益，它使得直接在上位反馈电阻并联零点的做法没有作用。 因此需要在快通道的LED电阻直接并联RC网络，并联后，原本LED电阻的位置上阻抗变为

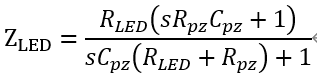
完整的传函变成

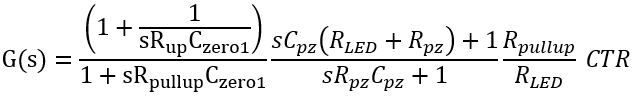
可得到两对零极点的位置。 如果零点和极点的位置都重合，可以求出

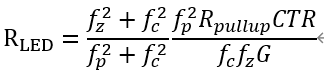
G为期望的交叉频率处增益。 之后就可以根据零极点位置求出RPZ和CPZ的值。

一般不会用TL431搭建这种补偿器，因为LED电阻对零极点位置存在影响，还是用运放搭建较好。

TL431偏置电流

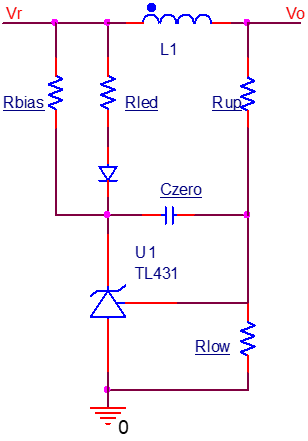
431需要一个从阴极流入的电流满足要求，必须大于1mA，否则其开环增益会大大减小，使稳压效果变差。 一般不能依靠LED电阻提供的电流，因为光耦的CTR会使期望的电流衰减，最后不能达到1mA的要求，所以应该另外增加偏置电阻，通过输出电压直接拉一个电阻到TL431阴极，或者在LED两端并联一个电阻都是可行的。

在仅仅靠LED电流提供偏置时，要考虑最大的光耦传输比。 先计算光耦输出端需要的电流值为

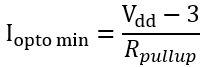
其中Vdd为控制器的逻辑电平，3V是假定反馈引脚的电压上限值。 则LED的电流最小可能是

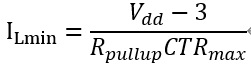
假设Vdd=5V，上拉电阻10k，CTR最大为100%，此时电流200μA，不满足要求。 所以要加入偏置，由最小电流要求得到偏置电阻的取值

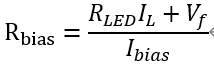
其中Vf为LED的压降，典型值为1V。 若要求偏置电流2mA，LED电阻2.2k，Vdd=4.8V，CTR取典型值为30%，得到偏置电阻为830Ω。

此外还有一个地方的偏置电流需要注意，即从电阻分压过来的电流，进入TL431的参考节点。 进入该节点的电流数据表给出为2~4μA，据此可以计算低端电阻值

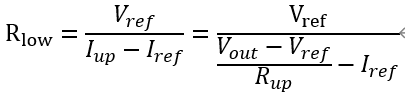
不过如果选择高端电阻的电流远大于μA级别，比如为1mA，就可以忽略这个电流值了。 对于低功耗应用来说，还是应当设定为更低的电流值，这时需要考虑这个电流的限制。

关于光耦

光耦的输出端中，集电极和基极之间存在较大的电容，会影响可用带宽，此带宽由电容和上拉电阻共同决定。 从数据表中给出的下降时间和测试电阻值可以计算出结电容值

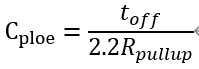
一般为nF级别。 因此对要求较大带宽的电源，光耦会造成较大的影响，或者使用阻值很小的上拉电阻。

另外，光耦还存在着一个高频的极点。

跨导放大器

输出电流为两个输入电压差的倍数。 特别之处在于跨导放大器不存在局部反馈，相当于开环运行，输入端也没有虚地的情况，而且分压电阻的下位电阻在环路中起作用。 常在PFC中应用。