基于FPGA进行DNN设计经验总结

深度神经网络（deep nearal network）是机器学习发展20年来取得的最大突破，比如在语音识别方面，相比于传统方法，其将错误率降低了30%；

而在2011年的图片识别竞赛上，将错误率从26%降低到3.5%，这些使得处于发展低谷的人工智能突然热门起来，从学术界扩展到工业界，甚至在google的alpha go击败了顶级围棋大师李世石后，人工智能成为全民讨论的热门，所有的程序员都梦想转行机器学习。

DNN中应用最广泛的是CNN和RNN，CNN是一种卷积网络，在图片识别分类中用的较多，RNN可以处理时间序列的信息，比如视频识别和语音识别。

这些DNN结构通常很深，计算量也很大。比如VGG16用来处理1000种图片类别，有550MB的权重数据，完成一个分类就需要31Gop（operations）。

为了降低计算量和访问内存时间，有两种方法：量化和降低权重。量化是减小权重或者激活数据的精度，比如从32bit浮点量化到8bit甚至1bit，就减小了数据量。降低权重包括剪枝和结构简化，这两种方法可以去除多余的权重参数。

DNN包括训练和推理两个阶段，训练是一个学习过程，通过不断的对权重进行迭代更新而使得网络获得智能。而推理阶段是给出一定输入后，网络会根据之前学习到的知识，输出准确结果。

为了使得结果具有更高准确率，训练是进行浮点运算，同时涉及到大量的微分运算，所以训练通常由GPU完成。但是训练是一次性的，当训练完成，网络就可以直接用于推断而不需要再进行训练。

FPGA就是用于推理过程，相比于CPU，具有更加灵活可编程的特点。可以针对DNN的特性增加运算并行度，调整内存访问，比CPU获得更高的实现效果。本章对自己基于FPGA进行DNN设计的经验做一个总结，包括对网络模型的一些体会，以及FPGA设计架构的一些思路，抛砖引玉。

1

DNN模型

不论是CNN还是RNN，一个共同特点是整个网络是由几个相同的单元联结形成的。CNN中基本的单元是神经元，一个神经元包含一个权重和激活函数，其中权重是对输入信息进行卷积（图1.1），几乎大部分运算量都集中在卷积运算中。

激活函数是对卷积后的结果进行非线性运算，激活函数有很多，像Relu，sigmoid等。基本的CNN网络结构如图1.2，网络每层都由多个神经元构成，每个神经元的输入来自上一层的输出，本层输出作为下一层的输入。

每层的输入通道是上一层神经元的个数，输出通道是这一层神经元个数。每个神经元对应不同输入通道的数据都有不同的权重数据（即kernel），这些权重和对应输入通道的图像完成卷积之后再求和，最后通过非线性激活函数给出输出通道的值。我们用伪代码来表示一层网络的运算过程：

For(int o=0;o

其中内四层循环是图像和权重的卷积运算，FPGA就是利用这6层循环进行加速。从这伪代码中可以看出每个乘法都是相互独立的，不会依赖于其他运算，而加法包含两种，一种是在卷积运算中，另外一种是每个输入通道卷积后的数据要求和。

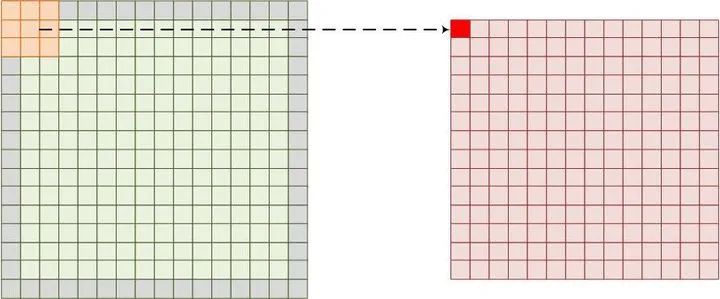
图1.1 图像卷积

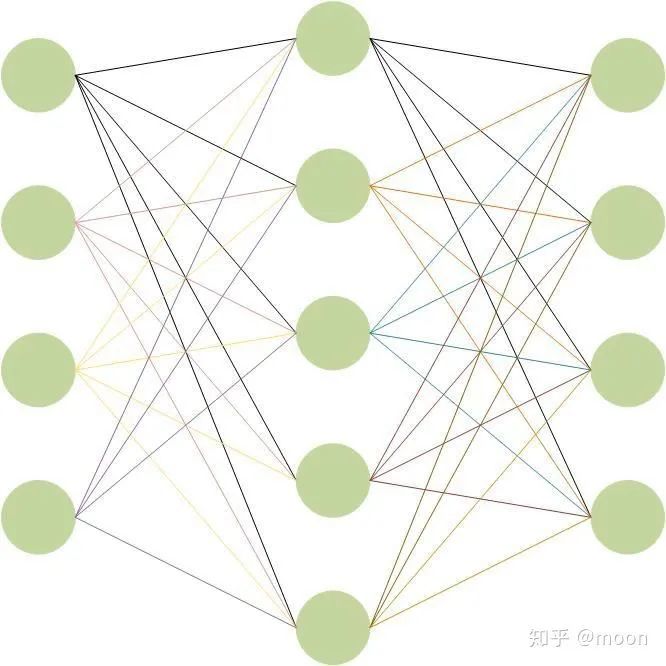
图1.2 CNN网络结构

另外一种比较常用的网络是RNN，这是一种循环神经网络，具有记忆功能，可以处理时序信息。这里重点介绍一下LSTM网络，LSTM也是一种RNN。但是其增加了多个门控：记忆门，输入门，输出门等。这些门解决了梯度消失和发散的问题，能够处理更长时序的信息。所以在语音识别和视频识别方面有重要应用。LSTM原理的介绍可以参见本公众号历史文章《LSTM原理》。FPGA更多的关心其中有哪些运算，LSTM中主要包含矩阵乘法，向量求和，激活操作，向量点乘等。矩阵乘法消耗最多的运算资源，如何优化这种运算是FPGA实现加速的关键。

对于矩阵乘法，根据其乘法顺序有一下几种方式。

1） 小矩阵x小矩阵

A每次获得nxm块数据，和B的mxv块数据相乘，然后A移动nxm块，B向下移动mxv块，再次相乘并且和之前结果累加，当A移动到右端，B同时移动到底端，完成C中nxv矩阵块。A中数据复用率在V次。

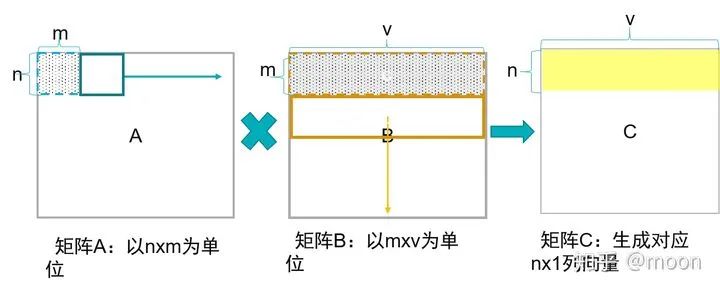
图1.3 小矩阵x小矩阵

2） 列向量x行向量

A每次获得nx1列向量，B获得1xn行向量，二者进行叉乘，得到nxn个矩阵数据，然后A向右移动，同时B向下移动，二者叉乘结果和上一次进行累加，最后当A移动到右端，B到底端，得到了一个nxn大小的C矩阵块。A中数据复用率在n次。

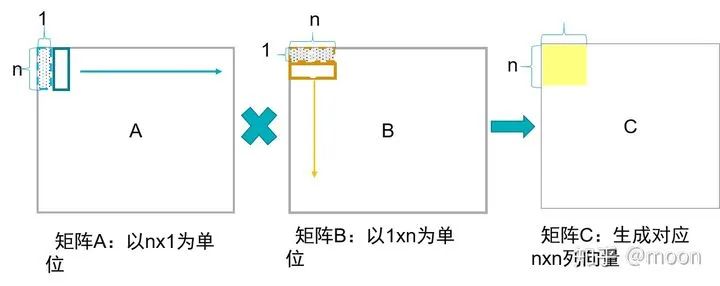
图1.4列向量x行向量

对比这两种计算方式，第一种A数据复用率取决于B矩阵列大小。A可以看做权重，B看做输入的图像或者声音信息，如果输入信息“宽度不够”，那么权重利用率低，就会造成运算比搬运数据慢，造成带宽瓶颈。第二种方式A仅仅需要n个数，就能参与n*n次乘法，利用率较高。这能够很大缓解带宽瓶颈。但是如果B的宽度较小或者B为向量，那么就会造成算力较低，搬运进n个数只能计算n次乘法。如何选择需要根据实际情况来决定。

2

量化和减少权重

虽然浮点数能够表示更高的数据精度和更大的数据宽度，但是浮点数据占用的存储资源和运算资源都较大，造成推理时间较长。随着网络的复杂和加深，对推理延时的要求越来越高，因此通过必要手段来压缩网络模型，降低推理延时显得非常重要。压缩网络模型主要有两种方式：量化和减少权重。

1） 定点化。

通过仿射变换将浮点数等效的映射到定点数空间，比如对于一个分布范围在（Xmin, Xmax）的权重数据，需要映射到（0，N-1）区间，其中N是定点可以表示的数据范围。浮点数就可以通过一个尺度和偏移量来表示为：

其中Z为0点偏移量，也是定点数据，S为尺度大小，用浮点数表示。在计算卷积的时候，就可以将尺度因子提取出来进行后处理，而乘法和加法运算使用定点完成。比如对于一个卷积运算可以表示为：

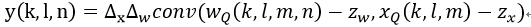
2） 二值化

二值化就是将参数量化到两个值{-1， 1}，和一个尺度参数。二值化网络大大降低了运算和参数存储，但是也对网络精度有很大削弱，所以应用范围很窄，比如用在MNIST和CIFAR-10这样比较小的数据集中。对于定点乘法一般都是用DSP实现，所以算力大小受到了FPGA中DSP数量的限制。而二值化网络的乘法运算可以通过简单的逻辑来实现，不在受限于DSP资源，可以大大提高算力。将浮点转化为二值有两种方式，一种是设定阈值，超过阈值设为1，小于设为-1。即：

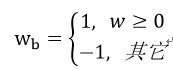
其中概率为：

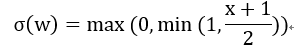
随机rounding不会导致参数分布发生偏移。

1） log量化

在一个2为底的对数表达中，参数被量化为一个2的幂次数据和尺度数。对数表达可以通过少量的bit位数涵盖宽阔的数据范围。比如3bit数据，最大为8，用2的幂次表达可以涵盖从0到255个数据范围。使用了log表达的乘法就可以用移位操作来实现了，这大大节省了DSP的使用。

量化的方式主要分为两种：一种是训练后量化，一种是在训练过程中量化。训练后量化省去了重新量化，但是可能对精度造成较大损失。训练过程量化，是在进行前向网络计算的时候，使用量化参数，而在反向传播过程中存储了浮点参数，更新浮点参数。过程如下：

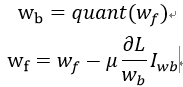
减少权重的方法也有很多，比如剪枝和结构化参数。剪枝是去除不重要的神经元连接，大大减少了权重数据，而结构化参数是通过设定阈值，让某一块的参数集体为0，这样降低了参数存储和计算量。这两种方法的详细介绍请见公众号之前的文章。

3

FPGA中并行方法

CNN中可以进行并行化运算的结构有：输入通道，输出通道，图像卷积。这其中输出通道之间是没有依赖关系的，而输入通道的结果是需要求和的。图像卷积每行输出像素之间没有依赖关系，但是每个结果像素是对应原来图像多个像素的。即一个卷积核涵盖大小的像素和对应卷积核相乘后累加。

神经网络中输入输出通道数量通常都较大，从输入输出通道上并行是一个很好的加速方法。比如我们选择4个输入通道和4个输出通道，如图3.1所示。

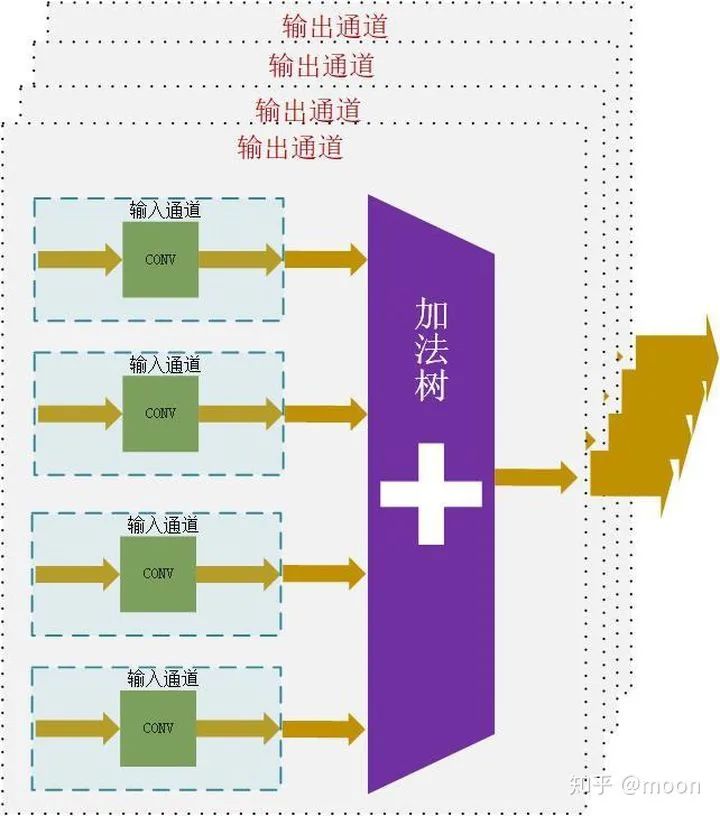
图3.1 输入输出通道并行化

这样就可以同时并行4x4个卷积运算，对于一个网络层为16（输入通道）x16（输出通道）的卷积运算，应用上述结构，就可以这样拆分来运算（图3.2）：每次都完成4x4通道运算，因为有16个输入通道，进行4次这样的运算，就可以输出4个输出通道数据。以同样方法进行4次就实现了16x16网络层的卷积运算。

因为输入通道之间需要求和运算，所以使用了加法树。随着输入通道变大，加法树级数会变深。假设使用2输入加法模块，那么上述4通道结构的加法树级数就是2。

在进行FPGA设计的时候这是一个需要考虑的问题，输入通道越多，加法树的fan-in越大，那么在高速时钟情况下，不同路径时间的延时就会影响时序性能了。如果输出通道变大，那么feature map数据的扇出就会变大，因为同一个feature map是被所有输出通道共享的。

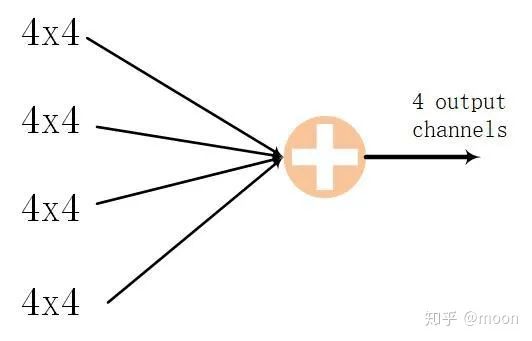
图3.2 通过4次4x4运算，然后求和完成4输出通道数据

输入输出通道的并行数收到了网络层大小以及fan-in和fan-out的限制，不可能太大。所以要增加并行度还需要继续探索图像卷积。首先我们想到卷积不是多个像素和卷积核进行乘法嘛，那么我们也将这些乘法并行起来就可以啦。但是这样存在一个问题就是：卷积核大小是不固定的，比如3x3卷积核中9个乘法被同时执行，那么等到了1x1卷积核，就会只有1个乘法器被使用，降低了乘法器利用率。因此这样并行不灵活。并行运算最好找到不存在依赖关系的运算。每行像素的输出是并行的，没有依赖关系的。那么就可以同时进行多行的卷积运算，而一个卷积核内的乘法和加法就可以用一个乘法器和累加器来做，这样就能适应不同卷积核大小的运算。多行并行运算如图3.3。

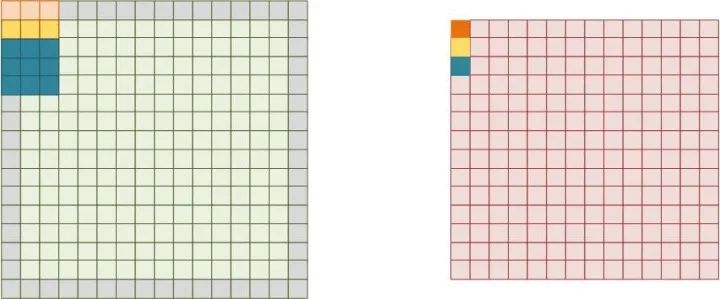
图3.3 3行卷积并行运算

采用以上输入输出通道的架构，缺点就是fan-out和fan-in较大，加法树级数较大。有没有什么方法可以降低fan-in和fan-out呢？如果将输入通道的求和也使用累加来实现，那就变成只有一个PE完成卷积运算以及不同通道的求和。但是一个PE却降低了并行度，那么可以想到增加串行的PE数量来增加输入并行度，即演变为一列PE来实现输入通道求和。由于PE排序上的空间限制，导致后边一个PE的计算相比于前一个PE要有1个周期延时，如果将数据从从PE间的移动打一拍，那正好可以在第二个PE计算出来的同时完成和前一个PE的求和，这就是脉动的关键所在。更具体的脉动阵列讲解请看公众号之前文章。

图3.4 加法树转化为脉动结构

4

存储结构

即使经过了量化和剪枝等处理，网络的参数也非常大（如表4.1），这在有限的FPGA资源下是无法全部存储于片上的。因此需要一个片外存储器（DDR）来存储权重和信息数据，在需要数据的时候从片外搬上片上来进行计算，并将结果存储到片外存储器。

表4.1 几种网络压缩前和压缩后大小对比

表4.2 几种Xilinx器件存储资源

这时候影响网络推理延时的因素就不仅仅包含算力的大小了，还需要考虑片上存储大小，ddr带宽，权重和信息数据复用率的影响。带宽和算力对推理延时的综合作用可以通过roofline图来表示。所谓“Roof-line”，指的就是由计算平台的算力和带宽上限这两个参数所决定的“屋顶”形态。

Roofline的纵坐标表示算力，屋顶代表了FPGA所能达到的最大算力，横坐标表示每byte数据可以参与多少次运算，表示了权重和信息数据的复用率。由roofline划分出两个瓶颈区域，一个是算力瓶颈，一个是带宽瓶颈。

当权重和数据复用率较高，即I大于FPGA所能达到的最大算力对应的复用率的时候，FPGA算力就是瓶颈，但是这种情况是好事情，因为FPGA的运算资源达到了100%的利用。

如果数据复用率较低的时候，那么带宽就成为瓶颈，因为在当前带宽下，载入到片上的数据无法支持最大算力，这时候FPGA运算资源利用率没有被全部利用，存在等待数据情形。

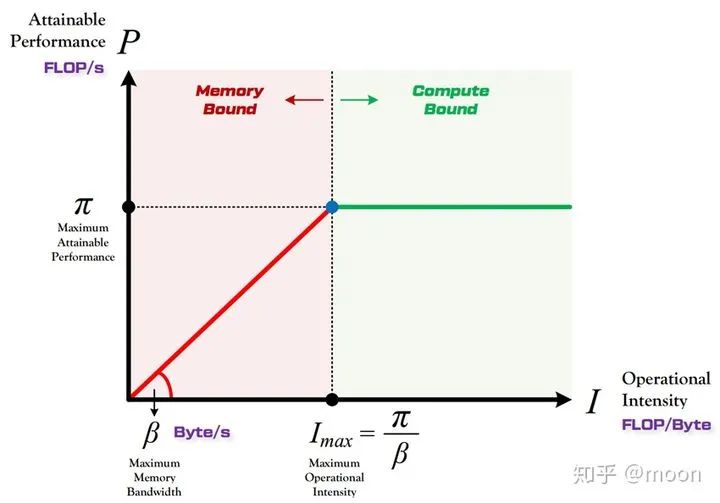
图4.1 roofline图

在一个CNN中，网络越往后图像大小越小，输入输出通道数量变大，这导致的结果就是权重参数的复用率变低，这个时候FPGA计算资源利用率就会降低。这个时候带宽大小以及片上存储就成为瓶颈。考虑片上存储后，通过一个简单模型来分析FPGA计算资源利用率。容易知道数据量和复用率同总计算量的关系：

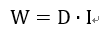
其中D为数据量，I为数据复用率。那么FPGA运算资源自用率就可以表示为：

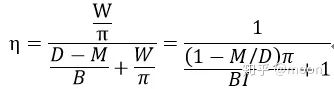
5

指令

指令实际上是一些控制FPGA流程的信息，比如载入多少数据，进行哪些运算（conv，pool等）。这些控制信息会根据不同的网络结构编辑好，存储成二进制文件放到ddr中。通过FPGA读入来控制操作。这些指令大体上包括以下几种：

1） load weights/image：从ddr中加载权重或者image数据到片上来。这其中会包含ddr首地址，需要读入的数据长度等信息。

2） conv：这个主要进行卷积运算，包括卷积核大小，图像大小，输入输出通道等信息。

3） activate：激活函数的控制，控制是否进行激活操作。

4） save image：将运算完的结果存储到ddr中，包括ddr地址，长度等信息。

总结

FPGA的灵活可配置结构非常适合不断变化的网络结构，同时其并行化和pipeline优势可以用于神经网络的加速。在进行FPGA设计的时候，需要考虑到并行化方式，存储结构，如何平衡带宽和算力之间的关系。