如何利用TINA-TI来完成跨阻放大电路的稳定性设计

在测试测量和医疗行业中，许多应用采集的原始信号都是光信号，例如LiDAR，OTDR，PCR等。在采集的过程中这类应用会不可避免的进行光电转换，首先通过光电二极管把光信号转化成电流信号，然后在通过跨阻放大电路把电流信号转成电压信号，之后再进行信号调理，最终输入ADC中。

其中跨阻放大电路的设计尤为关键，主要包括两方面，一方面是稳定性设计，一方面是噪声控制。接下来我们主要介绍如何借助TINA-TI来进行跨阻放大电路的稳定性设计。

一、 跨阻放大电路介绍

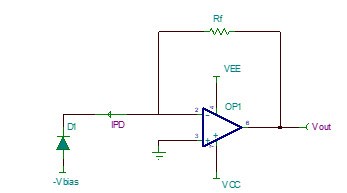
图  1 理想的跨阻放大电路

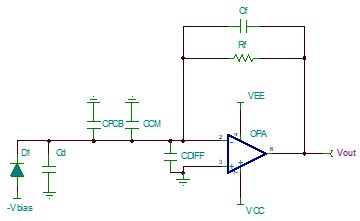
图  2 实际的跨阻放大电路

如图1所示，是理想的跨阻放大器电路，其工作原理如公式(1)所示。

但是在实际应用中，光电二极管会有一个从1pF至上百pF之间的寄生电容Cd。运算放大器的输入共模Ccm和输入差模电容Cdiff也需要考虑。除此之外，还有PCB的寄生电容Cpcb。

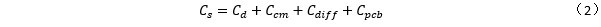
这时需要在反馈回路上加入反馈电容Cf，来对环路进行补偿。如图2所示。

最终可以等效为：

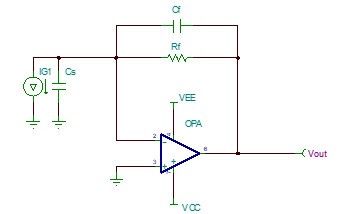
图  3 等效电路图

二、设计及仿真过程

仿真工具：TINA-TI。

在开始设计之前，我们要清楚Rf和Cs应该是已知的。

一般来讲，设计思路无外乎以下两种。

1）需要根据我们对跨阻放大电路的目标闭环带宽f-3dB去选出合适的GBP的运放和反馈电容Cf。

2）根据所选运算放大器的GBP，计算跨阻放大电路可以实现的闭环带宽f-3dB和反馈电容Cf。

为了便于理解，以一个开环增益为120dB，主极点为1kHZ运放为例，先从理想情况出发，逐步贴近实际情况。

1.理想的跨阻放大电路的稳定性分析

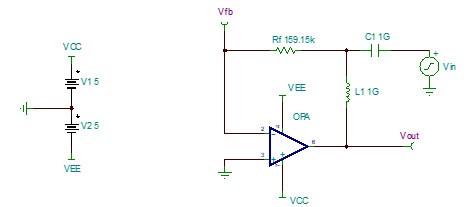
图  4 理想的跨阻放大电路

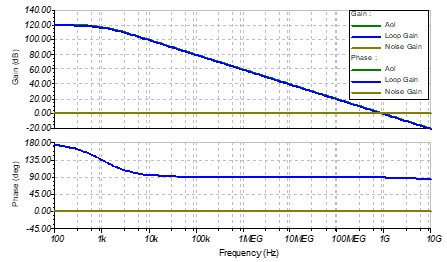
图  5 理想跨阻放大电路的伯德图

从伯德图，我们可以看出来，该运放的开环增益曲线Aol在1KHz处有一个主极点，使得Loop Gain以-20dB/dec速度下降，并在1GHz处穿越0dB，同时该主极点使Loop Gain的相位裕度等于90°，满足运放电路的稳定性判据，所以该系统处于稳定状态。

在对理想跨阻放大器的稳定性进行分析之后，让我们进一步考虑实际情况，把PD的结电容和运放的输入电容考虑进来。

2. Cs对跨阻放大电路的稳定性影响

我们假设全部的输入电容Cs=10pF，目标的跨阻增益是Rf=159.15KΩ。

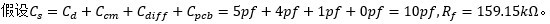
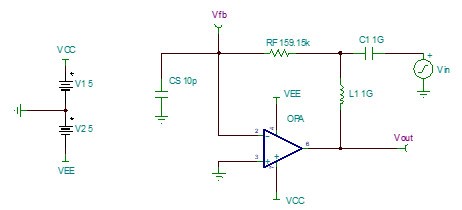
图  6  考虑Cs的跨阻放大电路

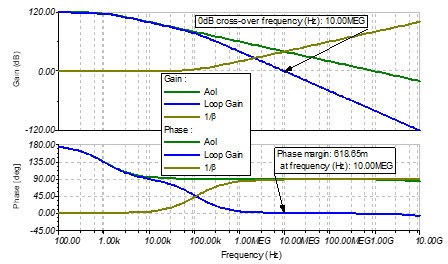
图  7 考虑Cs的跨阻放大电路的伯德图

首先观察一下幅频曲线：

噪声增益1⁄β即闭环增益随频率的变化。

在低频部分，10pF电容的阻抗非常大，可以认为是开路，运放会跟之前一样作为一个单位增益的同相放大电路，所以它的幅值为0dB.

随着频率的上升，输入电容Cs的阻抗开始下降，在100KHz处，Rf和Cs制造了一个零点1⁄(2π∙159.15kΩ∙10pF)=100KHz。噪声增益1⁄β将会以20dB/dec的速度上升。

从环路增益Loop Gain的角度出发，等价于开环增益Aol和噪声增益1⁄β相减，将会在环路增益Loop Gain中出现两个极点，等于0dB的点就是Loop Gain的穿越频率点。最终Loop Gain会以-40dB/dec的斜率穿越0dB，根据自动控制理论，那该电路将会处于不稳定的状态。

从相频曲线上看：

在环路增益Loop Gain 曲线上，1KHz处的主极点会带来〖90〗^°的相移，从100Hz处开始，在10KHz处完成相移。因为在100KHz处还有一个极点，相位会继续下降，从10KHz开始，并在1MHz处完成相移，所以在穿越频率点10MHz的相位裕度将会是0^°，根据自动控制理论，该电路将会处于不稳定的状态。

为了避免这种不稳定的状态，需要在反馈回路中加入一个反馈电容，所以接下来看一下引入反馈电容后，环路的稳定性将会发生什么样的变化。

3. Cf对跨阻放大器电路的稳定性影响

先假设反馈回路上并联了一个141fF的电容，后续会介绍如何计算反馈电容的容值。

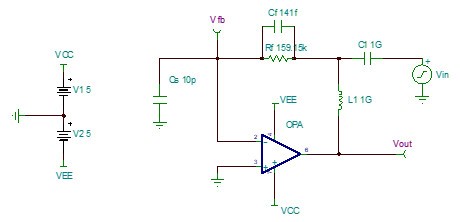
图  8 加入Cf后的跨阻放大电路

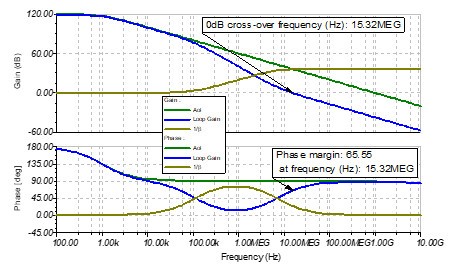
图  9 加入Cf后跨阻放大电路的伯德图

首先观察一下幅频曲线：

噪声增益1⁄β在低频部分，因为反馈电容Cf比输入电容Cs小很多，它不会影响由Rf和Cs产生的零点的位置。在高频部分，因为反馈电容Cf和反馈电阻Rf是并联关系，所以在高频部分反馈电阻Rf不再影响噪声增益，最终的噪声增益1⁄β由Cf和Cs决定，所以噪声增益1⁄β的幅度将不再变化。也就是说，在噪声增益的幅频曲线中引入了一个由Rf和Cf产生的极点，频率是1⁄(2π∙159.15kΩ∙141) fF=7.09MHz。

对于环路增益Loop Gain而言，R_f和C_f在Loop Gain在7.09MHz处引入了一个零点，所以反馈电容Cf的作用是与Rf构成零点，恢复环路增益Loop Gain曲线中的相位裕度。如图9所示，环路增益Loop Gain和噪声增益1⁄β交叉发生在15.32MHz，由于该零点的存在，从该零点频率的十分之一处700kHz开始，以45°/dec的速度增加。所以在环路增益的穿越频率15.32MHz处，环路增益Loop Gain恢复了足够的相位，从而获得了约65°的相位裕量。

将反馈电容Cf设置为远小于此141 fF的值将使Loop Gain中Rf和Cf形成的零点频率提高。例如当Cf=14.1fF时，从相频曲线上看，相位裕度低于理想值。

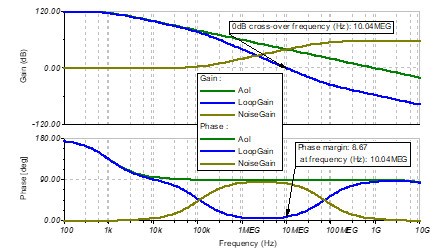
图  10 Cf=14.1fF 的伯德图

如果设置反馈电容Cf等于Cs，在噪声增益中，Cf和Rf形成的极点频率会接近于Cs和Rf形成的零点频率，这会使相位裕度接近于90°，如图11所示，最终导致系统的响应速度变慢。这里大家是否会有疑问，既然已经设置反馈电容Cf等于Cs了，那么为什么Cf和Rf形成的极点频率与Cs和Rf形成的零点频率不相等呢？

这是因为，噪声增益中的这个零点，是由Cs，Cf和Rf共同形成的，只不过当Cf远小于Cs时，我们可以把Cf忽略掉。

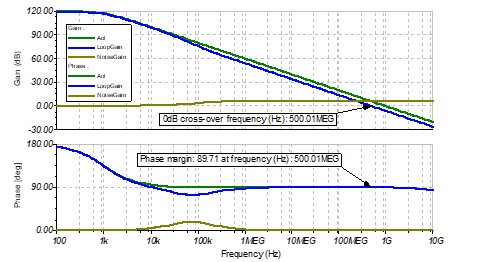
图  11 Cf=Cs时的伯德图

当设置Cf=70fF,141fF,280fF时，伯德图如下：

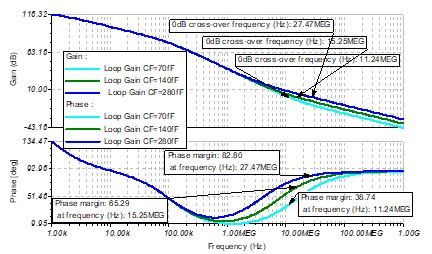
图  12 Cf=70fF,141fF,280fF的伯德图

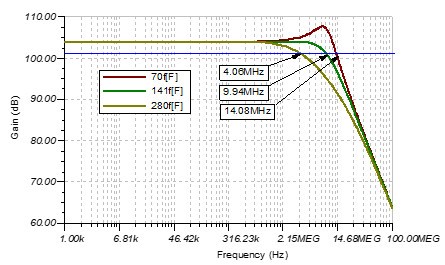
图  13 Cf=70fF,141fF,280fF的闭环传函的幅频曲线

可以看到，随着反馈电容Cf的增加，Loop Gain的穿越频率越来越高，相位裕度越来越高，闭环带宽越来越小。从闭环传递函数的角度上分析，反馈电容越大，Q越小，阻尼系数越大。与欠阻尼况和过阻尼相比，在临界阻尼情况下（Q=0.707），系统从受扰动以后，趋近平衡所需的时间最短。通过改变反馈电容的大小，可以改变相位裕度来控制脉冲响应或者改变闭环增益。

4. 设计流程总结

1）确定Cs，反馈电阻Rf，闭环带宽f-3dB。

例如，Cs=10fF，Rf=159.15 kΩ，f-3dB=10MHz

2）如果想得到巴特沃斯响应Q=0.707，根据公式（3），确定所需要的最小的GBP，根据结算结果，选择带宽合适的运放。

（3）

上面的公式是从何而来呢？可以参考一下《Transimpedance Considerations for High-Speed Amplifiers》，TIA电路的闭环传递函数是一个典型的二阶振荡环节，在获得巴特沃斯响应时，品质因数Q=0.707时，谐振频率fo=f-3dB。当根据TIA电路的闭环传递函数把fo的表达式写出来的时候发现，该频率点对应的是开环增益曲线和噪声增益曲线沿第一个零点过后延长线的交点。

需要注意的是，如果选择的运放的GBP比计算值大，那么在电路中计算时要按实际选择运放的GBP计算实际的闭环带宽。代入Cs=10fF，Rf=159.15 kΩ，f-3dB=10MHz，得：

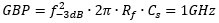
3）确定Cf。

同样的，参考一下《Transimpedance Considerations for High-Speed Amplifiers》，噪声增益曲线中反馈电阻R_f和反馈电容Cf形成的极点频率除以谐振频率fo等于Q，那么根据Q和f_o就可以求出Cf，而当Q=0.707时，fo=f-3dB：

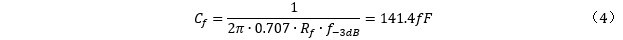
TI有一个Excel计算工具，可以帮助您完成设计，见《What you need to know about transimpedance amplifiers – part 2》

5. Decompensated amplifier在TIA电路中的应用

Decompensated amplifier是一种通过牺牲稳定性来提高性能的，单位增益下不稳定的运放。 与单位增益稳定运放相比，去补偿的放大器在使用更少的电流的同时，可以获得更高的增益带宽乘积，更低的噪声，更高的压摆率。

对于如图1 理想的跨阻放大器电路而言，只有反馈电阻的存在，这种情况下，噪声增益为1，那么对于decompensated amplifier而言，因为单位增益不稳定的原因，去补偿放大器是不适合这种情况的。

但是，对于实际的跨阻放大器电路而言，由于Cs和Cf的存在，将Noise Gain 将会稳定在（1+Cs/Cf），这样

1）确保了decompensated amplifier能够工作在稳定的状态。

2）因为decompensated amplifier的开环增益曲线相比单位增益放大器的开环增益曲线，向上和向右拓展，因此避免了使用单位增益放大器的Loop Gain 以-40dB/dec速度下降的可能，同时提高了该放大电路的闭环带宽。

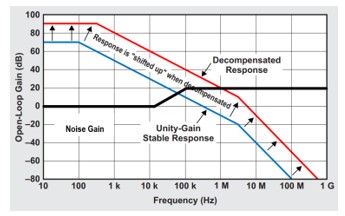
图  14 Decompensated amplifier与单位增益放大器开环增益的区别

所以Decompensated amplifier是天然适合跨阻放大电路的应用。

审核编辑：郭婷