简化电阻网络的策略

通过辨别串联式和并联式，我们可以把复杂的电阻网络变得简单。 这篇文章会用这个例子来系统地讲如何简化电路。

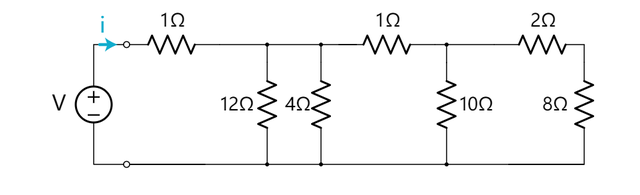
这个电阻网络连接着一个电压源。 左边的两个小圈代表电阻网络的端口。

假设我们想找出从电压源施加在电阻器网络上的电流是多少。 答案并不显而易见。 但是，我们可以利用一些工具：我们知道如何计算并联式和串连式的总电阻。 通过这些工具，我们可以一直简化电阻器网络直到问题的答案呼之欲出。

简化电阻网络的策略

从电路的最远端开始。

将任何串连式或并联式的电阻器替换为等值的电阻。

继续向左简化直到整个网络都能用一个电阻值来表示。

问题所问的位置就在电压源，所以我们简化的过程会从最远点开始，再不断接近电源。

简化电路包括了很多小步骤。 先从一段开始着手，简化，然后再考虑下一段。 提示：每简化完一次，重新画一幅电路图来确保你不会错过其它能简化的部分。

步骤1.处于阴影的电阻器2Ω,和8Ω呈串连式。

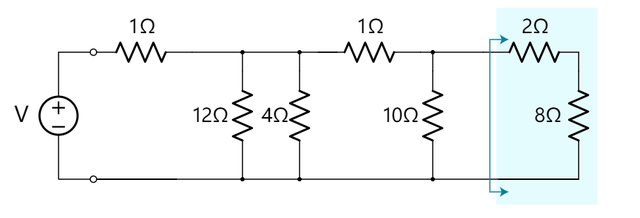
这两个电阻器呈串连式，所以我们将它们的电阻相加。

2 小时 + 8 小时 = 10 小时

两个电阻器可以视作具有同样电阻的一个电阻器。

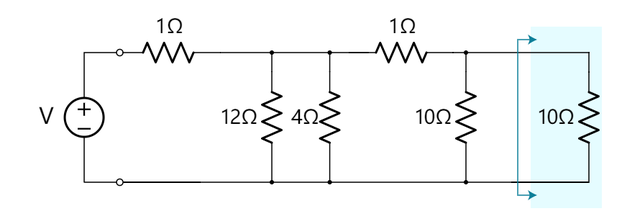
中心见解：阴影框外，两个串联的电阻器和它们的等值电阻并不能清楚地区分开来。 两者都具有等量的电流和电压。

步骤2我们现在可以在新电路的右侧上发现两个10 Ω的电阻器。

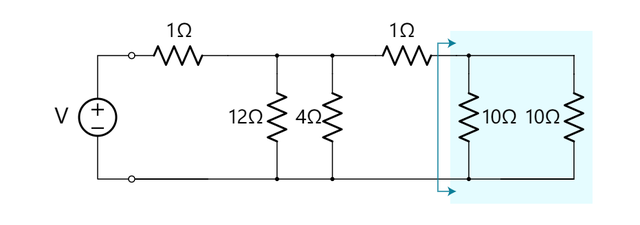
这两个电阻器可以被它们的串联式总和来替代。

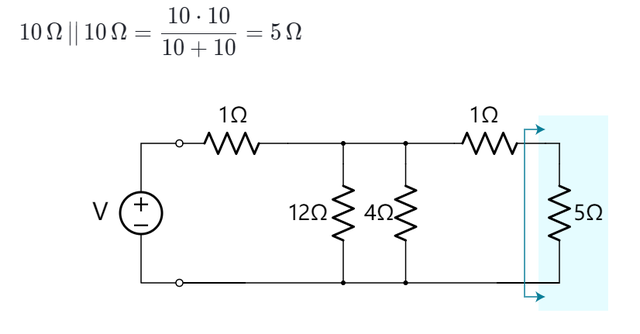
同样，从左边看阴影部分时，原电路的电流、电压，以及总电阻仍然不明确。

Step 3. 到这里可以渐渐看出一个规律。 我们在从右往左不断简化电路图的结构。 然后我们就会得到串连式的两个电阻器1 Ω和5 Ω。

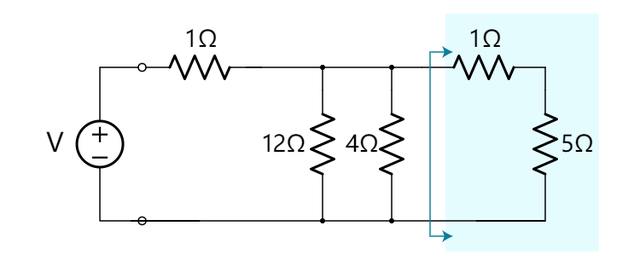
1Ω+5Ω=6Ω

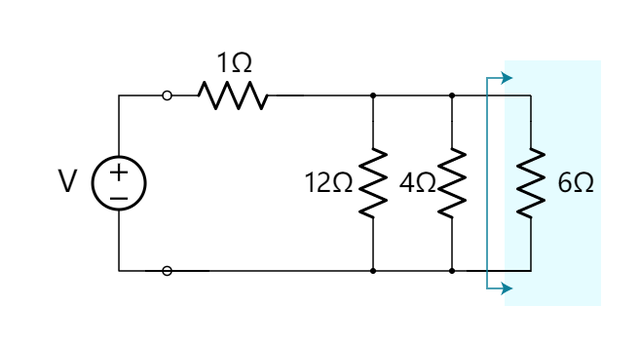
步骤4.这一步骤更具挑战性。 我们有三个并联的电阻器。

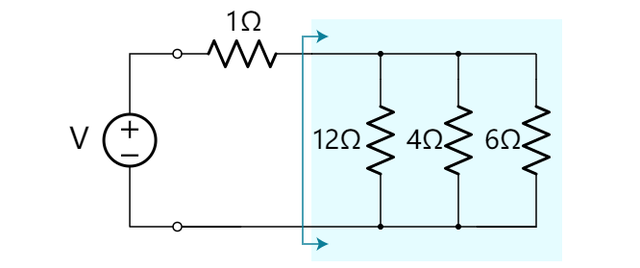
这些电阻器可以被它们的并联式总和来替代。

 

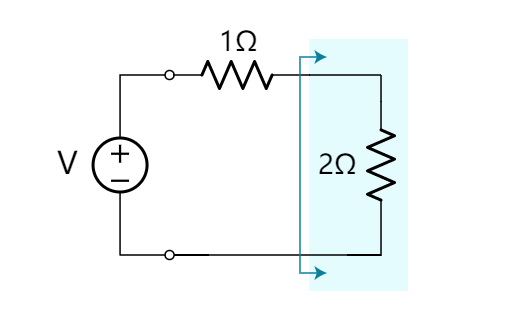
步骤5. 我们来到了最后两个串联的电阻器，

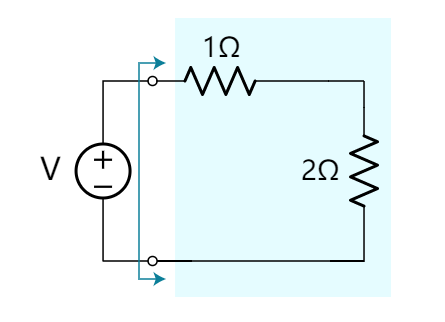
你可以直接想出答案：

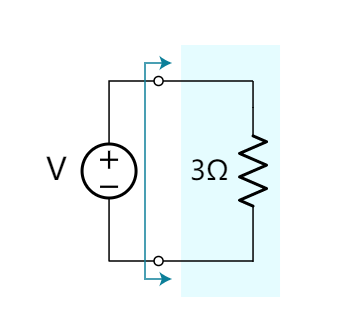
我们最后剩下了一个3Ω的电阻器。 从电源的位置来看，这个电阻器代表了整个电阻器网络。 从电源输出的电流是，

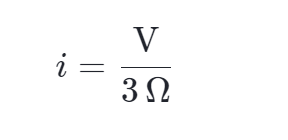
我们从7个电阻器一直简化到1个，干得不赖。

中心思想 : 简化策略为从未知点的最远端开始简化。

在这个例子中，我们需要求出左边电源处的电流大小，因此我们从电路的最右端开始逐渐向左分析。这种“反方向”解题的思路看上去很别扭，与我们平时从左看到右的阅读习惯相冲突。

在电子领域中，解题思路通常是从电路输出端（通常在右侧）开始逐渐往输入端靠拢。你“正常”的从左往右的阅读习惯可能会影响你看电路图时的思路。从现在开始，你需时刻警惕这个坏习惯可能造成的。

并非所有的简化都会最终只得到一个电阻器（电路可能不是完全由电阻器组成）。但只要有能简化的地方，不要犹豫，简化它。

例外

某些电阻器排列并不能用如上方法来简化，因此需要用其他方法来计算。这些例子将会在下面的文章中体现。