并联电阻的特性

如果元件共享两个节点 , 则它们是并联的。 例如：

本文中我们将通过并联电阻来学习并联这一连接方式的特性。 在以后的章节中我们将讨论电容和电感的串联和并联。

并联电阻

如果电阻共享两个节点，则它们是并联的。

在下图中，R1、R2和R3是并联的。 两个分布的节点由两个横向直线表示。

并联的电阻在它们的节点上有相同的电压。

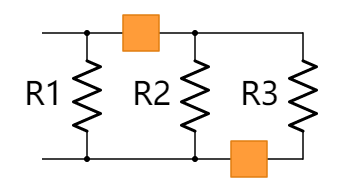
下图中的电阻不是并联的。 有额外的元件(橙色盒子)切断了电阻间的公共节点。 该电路有四个独立的节点，因此R1，R2和R3不具有相同的电压。

并联电阻的特性

解并联电阻比串联电阻稍微复杂一些。 这是一个并联电阻的电路。 (这个电路有一个电流源。 我们不经常使用它们，所以这应该很有意思。 )

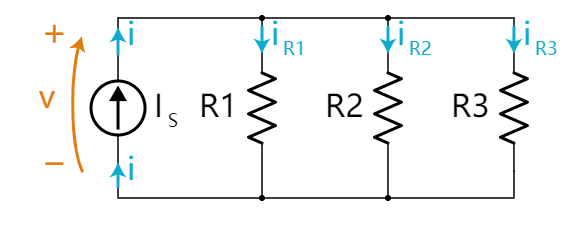
当前的电源Is将 电流i输入R1,R2和R3。 我们知道 电流i的值是给定的常数，但我们不知道 电压v和电流i是如何被分配到3个电阻上的。

我们知道的两件事是：

三个电阻通过的电流之和应该是i。

三个电阻具有同样的电压v。

这些式子提供了一个入手点。 重新排列三个欧姆定律表达式，用电压和电阻来表示电流：

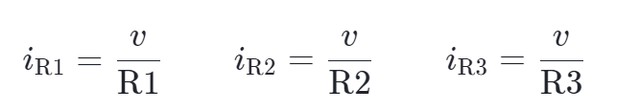
将它们带入到电流和的式子中：

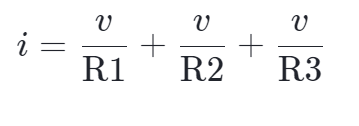
提取出共同项v

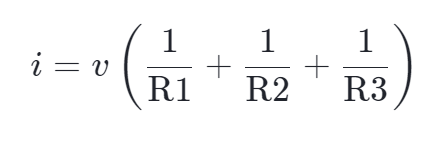
注意我们已知i（它是电流源的一个属性)，所以我们可以求出v

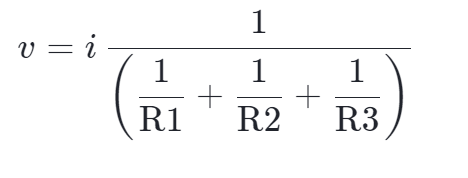
这个表达式看起来像欧姆定律，v=iR,，但并联电阻部分以一个双倒数的形式代替了单个电阻。

我们的结论是：

对于并联的电阻，总电阻是各个电阻的倒数之和的倒数。

(这看起来很复杂，但在结束之前我们会将其简化。 ）

等效并联电阻

前面的等式表明我们可以定义一个新的电阻，使其等效于并联电阻。 这里等效的含义是对于给定电流i，会产生与原电阻相同的 电压v。

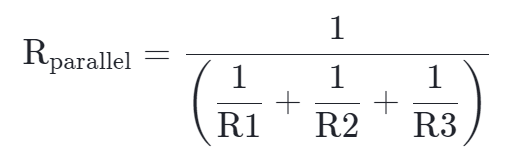
等效并联电阻是倒数之和的倒数。 我们可以通过重新排列这个吓人的式子，以另一种方式写出这个等式。

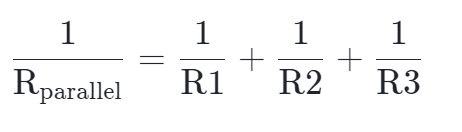
欧姆定律应用于并联电阻，

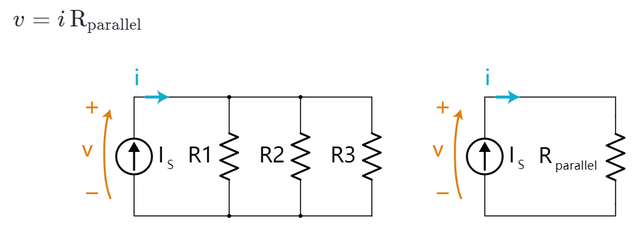
从电源的“视角”来看，等效电阻Rparallel与三个并联电阻没有区别。 因为在两个电路中，v是相同的。

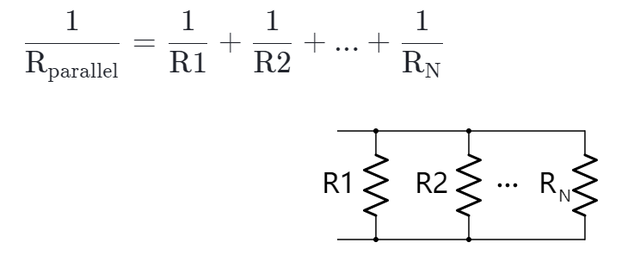
如果你有多个并联的电阻，那么等效并联电阻的一般形式是，

电流在并联的电阻之间的分配

我们已经得到了并联连接的每个电压v，下一步是求每个电阻的电流值。

通过对每一个电阻套用欧姆定律来进行。

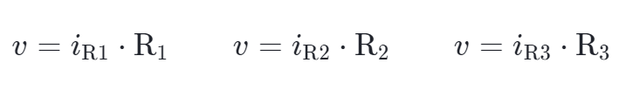
一个使用真实数字的例子可能会更直观。

计算通过三个电阻的v和电流。
解释流经各个电阻的电流之和是i的原因。

解问题的步骤是,

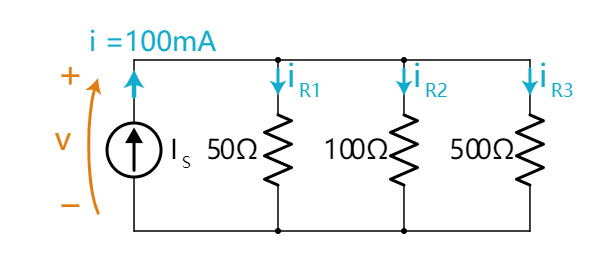
计算等效并联电阻Rparallel，

使用欧姆定律来计算电压v。

再次使用欧姆定律来计算单个的电流。

将电阻电流相加得到应该的值以验证。

等效电阻Rparallel等于三个电阻各自的倒数之和的倒数。

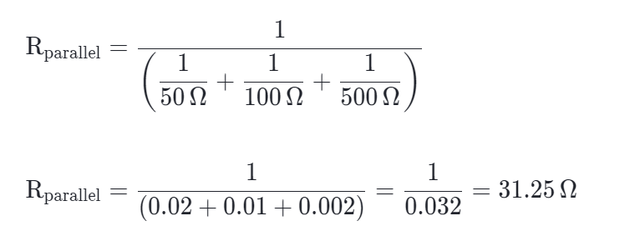
现在我们得到了等效电阻。 我们可以计算两个节点之间的电压v

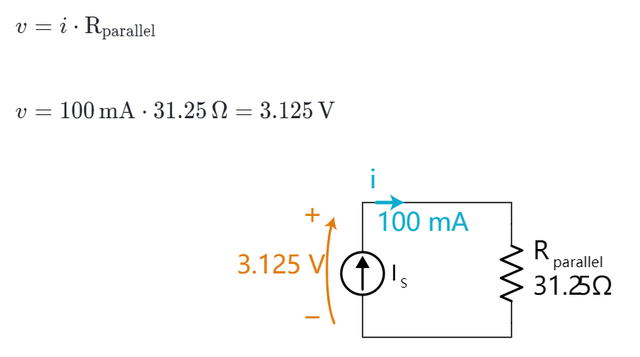
得到v后我们可以计算单个电阻的电流，

 

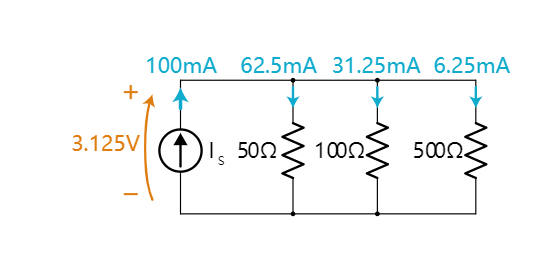
检查:各个电阻电流之和是否等于电源电流？

62.5 毫安+31.25 毫安+6.25 毫安=100 毫安 ✓是

电子会选择通过哪一个电阻

关于并联电路的一个常见问题是，“电子如何'选择'流过哪个电阻"，或 “电子如何'决定'流向何处？ "

我们都知道，电子不是人。 它们没有大脑(据我们所知)。 因此，他们不会选择或决定流过哪个电阻器，如同水分子“决定”当它流过岩石中的一条河时将流向哪一侧。

在并联电路中，每个电子仅响应来自电压源和来自周围电子群的相斥电磁力。 其中不包含任何决定。

特例-两个电阻并联

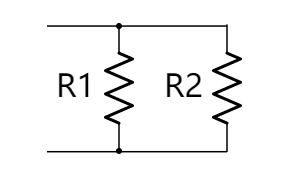
两个并联的电阻的等效电阻值为:

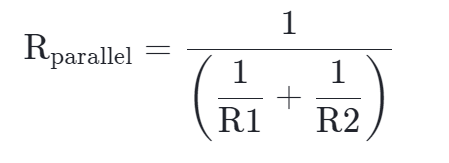
可以做一些操作来消除倒数，并得出只包含一个分数的表达式。 我们不会直接告诉你答案。 这是让你初次使用代数方法解决问题的挑战。 答案是隐藏的，所以你可以在偷看之前自己尝试一下。

两个电阻并联

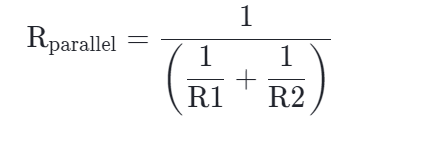
继续处理分母以简化分数。 共同分母是R1⋅R2

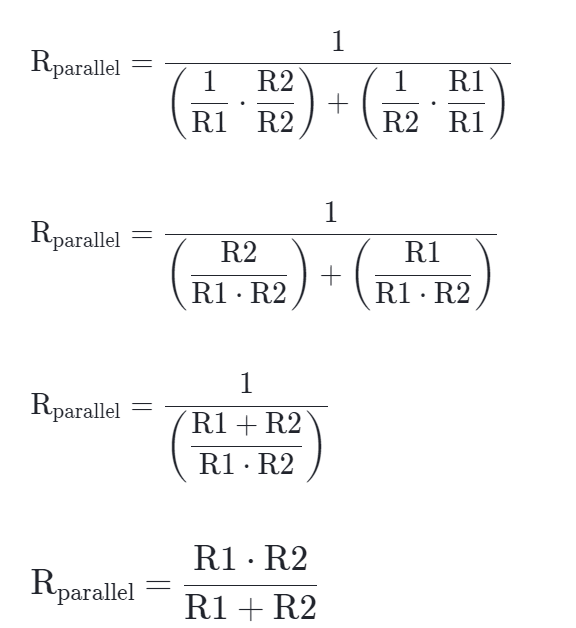
这是两个并联电阻的等式。

求和之上是乘积，这个值得记住。

特例-两个相等的电阻并联

如果两个并联的电阻阻值相等，等效并联电阻Rparallel是多少?

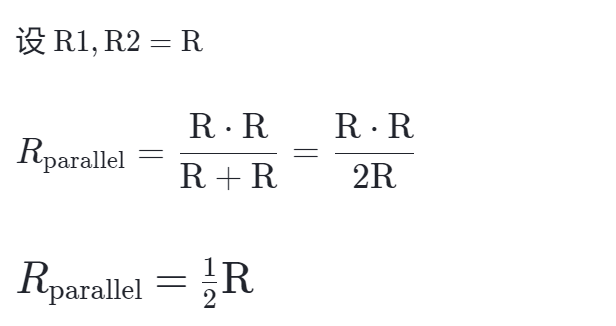
两个相同的并联电阻的等效电阻等于任一电阻值的一半。 电流在两者之间平分。

总结

并联的电阻共有相同的电压。

三个或三个以上的电阻并联后的等效电阻是，

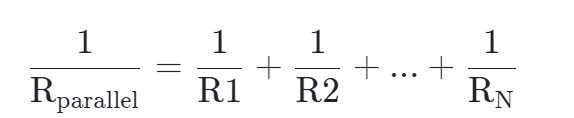
如果是两个电阻并联，可以很容易地将它合并成乘积除以和。