

PLC中随机数产生的几种方式
描述
有时为了某些测试需求,需要仿真产生一些数据。 这时,我们可以通过调取指令或自行编写程序来生成这些随机数据。
以下以博途为例,简要说明了随机数产生的几种方式:
一、读取系统时间的纳秒作为随机数
以固定周期直接将系统时间中的纳秒输出到对应变量。
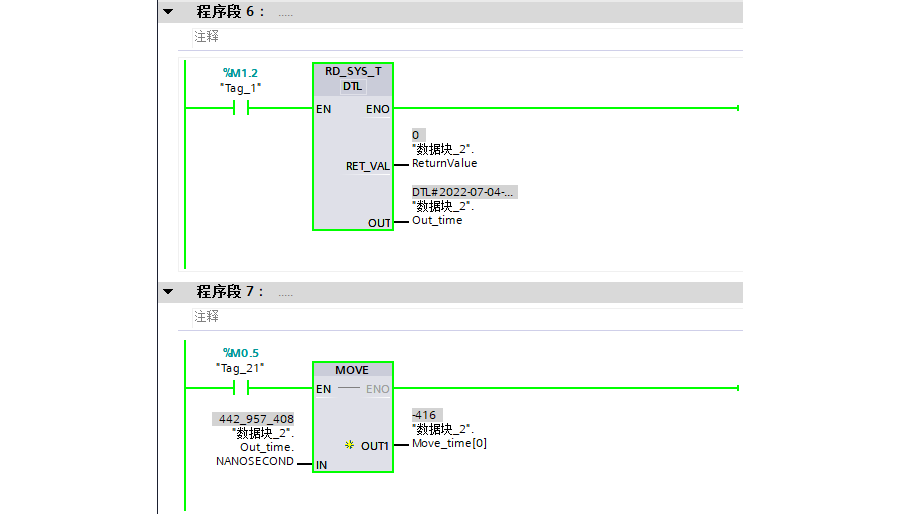
系统时间中的纳秒为UDINT类型,转为INT后,丢弃了高字部分

监视实时的系统时间,取其中的纳秒(NANOSECOND,1秒=10^9纳秒)

监视一下生成的随机数的范围:-32258—32751(5分钟)
后续可继续对此数据处理,缩放到需要的区间。
二、由LGF库(官方提供的通用函数库)内的随机数程序生成
该指令原理也是采用纳秒,不过处理过程更加细化、完善。

LGF库
随机数生成程序如下(只贴了其中关键的计算过程):
REGION Calculating random number
// 将纳秒转换为双字以便寻址单个字节
#tempNanoSecondInDWord := UDINT_TO_DWORD(#tempTime.NANOSECOND);
// 以片段访问方式将纳秒进行字节交换
#tempRandomValue.%B3 := #tempNanoSecondInDWord.%B0;
#tempRandomValue.%B2 := #tempNanoSecondInDWord.%B1;
#tempRandomValue.%B1 := #tempNanoSecondInDWord.%B2;
#tempRandomValue.%B0 := #tempNanoSecondInDWord.%B3;
// 随机数标准化
#tempNormReal := UDINT_TO_REAL(DWORD_TO_UDINT(#tempRandomValue)) / UDINT_TO_REAL(#MAX_UDINT);
// 随机数缩放
#LGF_RandomRange_Real := ((#tempNormReal * (#maxValue - #minValue) + (#minValue)));
#error := false;
#status := #STATUS_FINISHED_NO_ERROR;
#subfunctionStatus := #SUB_STATUS_NO_ERROR;
// ENO mechanism is not used
ENO := TRUE;
END_REGION

在主程序中调用,可设置上下限
三、线性同余法(LCG,Linear Congruential Method)
该方法的核心是以下递归公式:
RandNum =(A * RandNum + B)% M
A、B、M均为常数,其中A是 乘数 ,B是 增量 ,M是 模数 ,RandNum是 初始值 ,A、C、M的取值是保证产生高质量随机数的关键。
可以看出,每次新产生的随机数都跟上一次的数有关系。 随机数序列中的初始值,我们通常叫做种子。 随机数的产生需要设置种子,否则随机数的结果每次运行都将一样。 通常,我们使用系统时间的纳秒作为种子(某些将此作为缺省设置),这在一定程度上保证了种子的唯一性。
由于计算过程最后是对M取余数,余数的范围就是0—(M-1),这决定了产生的随机数是有周期性的。 M的大小决定了最大周期的长短,一般取值域的最大值,而A和B也会影响周期。 A、B、M的选取多种多样,只要保证产生的随机数有较好的均匀性和随机性即可。

FC块,变量定义为双整型。 模数M可以取值域最大值2^32

种子seed可以采用系统时间或自行设置

随机数曲线
线性同余法的初始值一旦确定,输出的序列将固定。 而当获取某些随机数序列后,其初始值以及A、B、M也会被反向计算出来。
对于其缺点,可以考虑以下改进方式,每产生n个数,将当前时钟值MOD M得到的余数作为新的种子。
四、平方取中法
平方取中法由冯·诺依曼提出,它的原理是:首先取一个2s位的整数(种子),平方,得4s位整数,然后取此4s位中间的2s位作为下次运算的种子。 重复该过程,即可得到一个随机数序列。 (序列中每个数缩放至0.0—1.0范围内)
例如:取种子365,平方得133225,高位补0,取中间1332,平方得1774224,高位补0,取7742,以此类推.........

#RandInt := SQR(#Seed);
#Seed := (#RandInt MOD 1000000 - #RandInt MOD 100) / 100;
#RandReal := DINT_TO_REAL(#Seed) / 9999.0;

随机数测试结果
在实践中,这种方法其实并不好用。 很难说明取什么种子才能保证足够长的周期。 以种子123为例,在40多个周期后,种子末位便退化产生了00,之后的随机数成了固定的几个数值,周期极短。 该算法也有改进空间。
梅森旋转算法_Mersenne Twister
梅森旋转算法可以产生高质量的伪随机数,且效率高效,弥补了以上伪随机数生成器的不足和缺陷。 它在C++、Python等编程语言中均有应用。
理解该算法前需要先了解许多前置名词,线性反馈移位寄存器、级、反馈函数、抽头序列、本原多项式...... 实在有兴趣的可以搜索一下。 我,放弃了。
说到随机数,不禁想到了因果律:果由因生、有依空立 、事待理成。
所谓的“随机”,大概不过是事物发展中的个体因为信息偏差,产生的局限认知。
-
真随机数和伪随机数的区别2025-08-27 1987
-
AT32的随机数的产生2023-10-26 839
-
PLC输出0~100之间的随机数编写2023-10-11 6368
-
STM8单片机产生随机数2021-11-23 1004
-
产生随机数的方法有哪些2021-07-15 1810
-
单片机C语言如何产生随机数2019-11-26 8054
-
单片机产生随机数的两种方法2019-03-01 2752
-
单片机产生随机数的方法2019-02-23 22782
-
随机数产生小程序求助2018-04-18 4102
-
产生随机数2016-12-01 1214
-
STM32的ADC产生随机数2015-02-28 11767
-
怎么产生更大范围的随机数?2013-10-26 4027
-
keil 产生 随机数2013-03-12 21751
全部0条评论

快来发表一下你的评论吧 !

