

数字电路基础知识之加法器、减法器
电子说
1.4w人已加入
描述
0****1
二进制加法器
01
半加器
半加器不考虑低位进位来的进位值,只有两个输入,两个输出。由一个与门和异或门构成,
真值表如下:
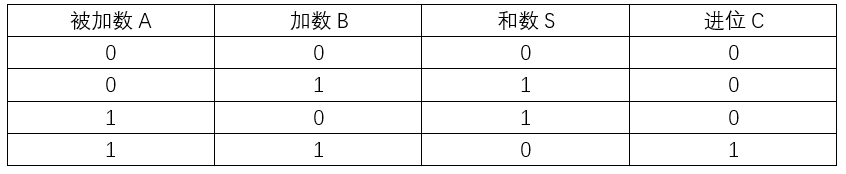
逻辑表达式 :

02
全加器
当多位数相加时,半加器可用于最低位求和,并给出进位数。第二位的相加有两个待加数和,还有一个来自前面低位送来的进位数。这三个数相加,得出本位和数(全加和数)和进位数。这种就是“全加"。
**真值表如下: **
| 被加数A | 加数B | 进位输入Ci | 和数S | 进位输出Co |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
逻辑表达式 :

经过上面的介绍我相信大家对加法器已经有了一定了解,接下来我们为大家介绍如何用与非门等设计一个全加法器。首先我们需要对 公式化简 ,这里就用到了前面介绍的逻辑转换律。
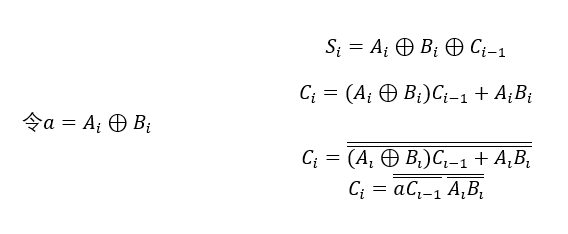

02
减法器
减法器可以由基础的半减器和全减器模块组成,或者基于加法器和控制信号搭建。
定义Nbit被减数x,减数Y,差为D(difference);来自低bit的借位Bi,想高bit借位Bi+1,i为bit序号。
01
半减器
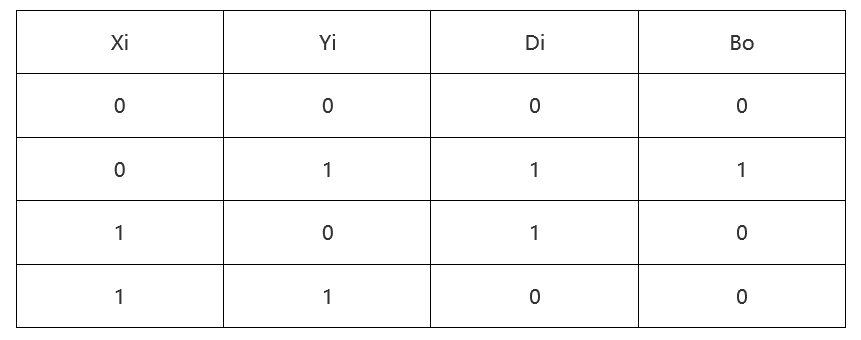
半减器用于计算两bit Xi和Yi的减法,输出结果Di和向高位的借位Bo(Borrow output)。其真值表、逻辑表达式如下:
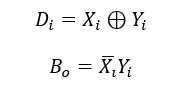
02
全减法器
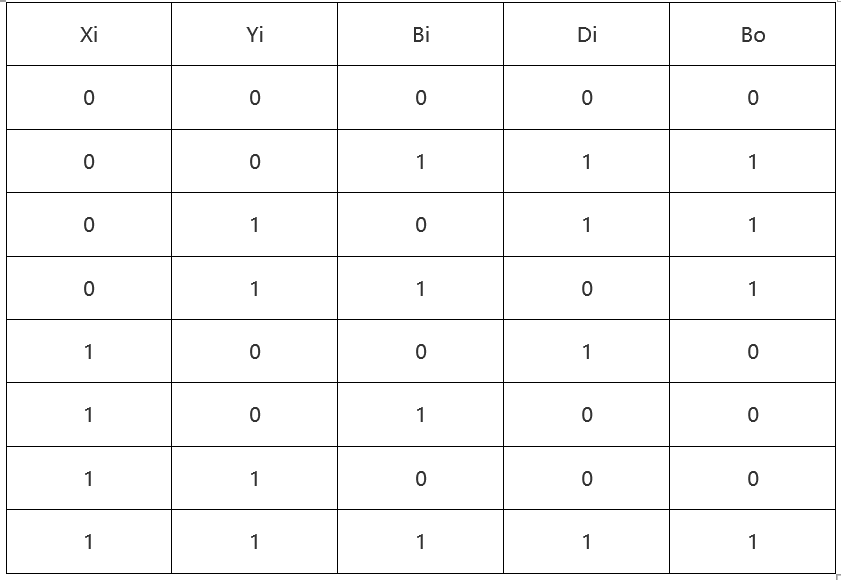
全减器不同于半减器在于,全减器输入来自低位的借位Bi(Borrow input),另外两个输入xi、yi,输出为Di和向高位借位Bo。
其真值表、逻辑表达式如下:
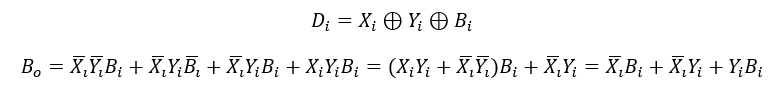
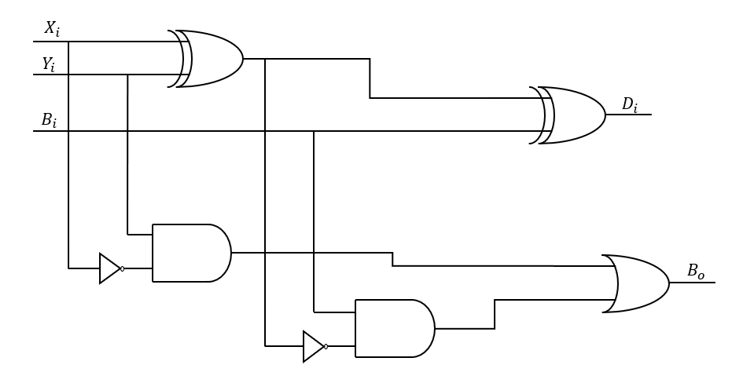
接下来我们为大家介绍如何用与非门等设计一个全减法器:
03
乘法器(阵列乘法器)
实现乘法的比较常用的方法是类似与手工计算乘法的方式:

对应的硬件结构就是阵列乘法器(array multiplier)它有三个功能: 产生部分积,累加部分积和最终相加 ,其中HA为半加器,FA为全加器。

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
加法器的原理是什么 加法器有什么作用2024-05-23 7830
-
减法器电路与原理 减法器电路图分享2024-02-19 12179
-
镜像加法器的电路结构及仿真设计2023-07-07 5167
-
半加法器的工作原理及电路解析2023-06-29 14327
-
加法器的原理及采用加法器的原因2023-06-09 6467
-
数字电路中加法器和减法器逻辑图分析2020-09-01 24701
-
12位加法器的实验原理和设计及脚本及结果资料说明2019-04-15 2920
-
加法器与减法器_反相加法器与同相加法器2017-08-16 169737
-
同相加法器电路原理与同相加法器计算2016-09-13 58860
-
8位加法器和减法器设计实习报告2013-09-04 2679
-
带输入缓冲的减法器电路2010-09-04 3224
-
本的二进制加法/减法器,本的二进制加法/减法器原理2010-04-13 5483
-
加法器,加法器是什么意思2010-03-08 5889
全部0条评论

快来发表一下你的评论吧 !

