

电桥电路的等效分析
描述
电路分析的核心 - 电路等效
百度百科有云:等效电路是将一个复杂的电路,通过电阻等效、电容等效,电源等效等方法,化简成具有与原电路功能相同的简单电路。 这个简单的电路,称作原来那个复杂电路的等效电路 。
我们可以毫不夸张地说,等效电路是电路分析的核心。
电阻的等效
两个电阻串联,可以等效为一个电阻,其阻值为两个电阻阻值之和。 两个电阻并联,可以等效为一个电阻,其阻值的倒数为两个电阻阻值倒数之和。
电感的等效
两个电感串联,可以等效为一个电感,其感值为两个电感感值之和。 两个电感并联,可以等效为一个电感,其感值的倒数为两个电感感值倒数之和。
电容的等效
两个电容并联,可以等效为一个电容,其容值为两个电容容值之和。 两个电容串联,可以等效为一个电容,其容值的倒数为两个电容容值倒数之和。
举个栗子:如下电路的等效电路。
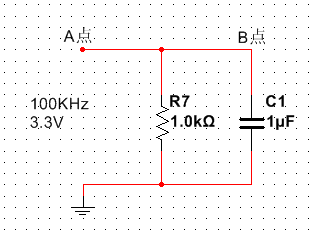
电容与电阻并联起来后,由于电容的阻值随着频率变化而变化,所以该电路的等效模型,在不同的频率下也不一样。
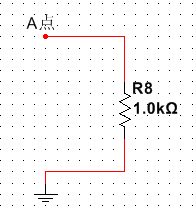
若A点接直流源,则频率为0,电容成开路状态,电路中只有1K电阻起作用。
故A点接频率为100KHz的电源,C1阻抗Z=1/(23.141KHz*1uF)=1/0.00628=159.24Ω。
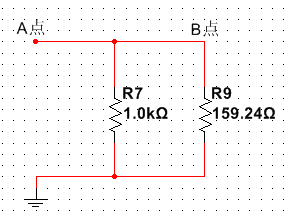
电路在100KHz下,相当于1K与159.24Ω的并联。
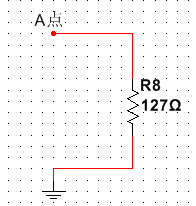
若A点接频率为1GHz的电源,C1阻抗约为0Ω,整个电路等效为电源短路。
电桥电路的等效分析
下图所示的电路,被称为“惠斯通电桥电路”,广泛应用在电阻精密测量设备中。
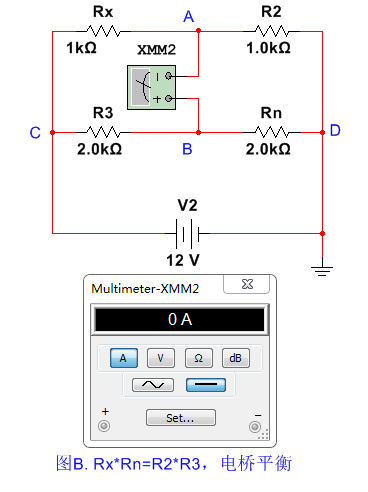
Rx为被测电阻,Rn为可调精确电阻。R2和R3为定值电阻。XMM2为高精度电流表。 1 ) 若 Rx/ (R2+Rx )=R3/ (R3+Rn ) 时,
2 ) 根据串联电阻等比例分压原理,A**点对地电压等于B 点对地电压 。
3 ) 故AB 两点之间压差为0 ,电流表中无电流流过,我们称为“电桥平衡”。
4 ) 根据此原理,通过调整Rn的阻值,观测电流表指针,当指针归0后,由于R2、R3、Rn的值都是确认的,就可以 根据公式Rx= (R2R3* )/Rn ,计算出待测电阻Rx 的值 。通过调节R2和R3的阻值,可以实现mΩ-MΩ电阻的精确测量。
若电桥不平衡,则A点电压不等于B点电压,AB之间有电流流过。
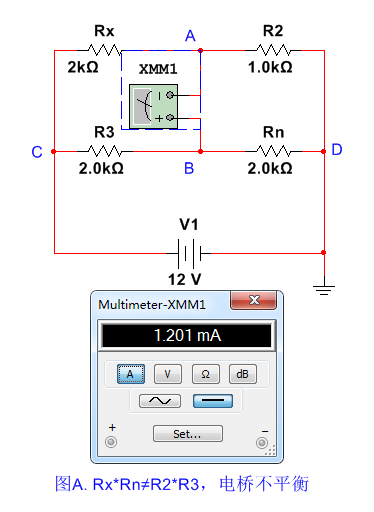
若用一个等效电阻R10替代掉电流表XMM1,电路就成下图所示,这时候再来求解C-D之间的等效阻抗是多少,该怎么来求呢?
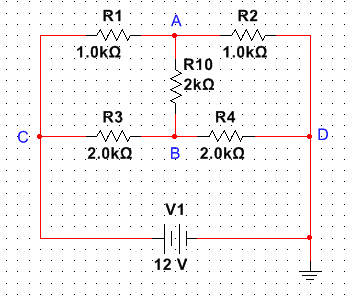
上图中,
R1、R10、R3组成△形电路;
R10、R3、R4组成了Y形电路;
R2、R10、R4组成△形电路。
若要分析类似上图中的电路,就需要掌握△形电路和Y形电路之间的电路变换。
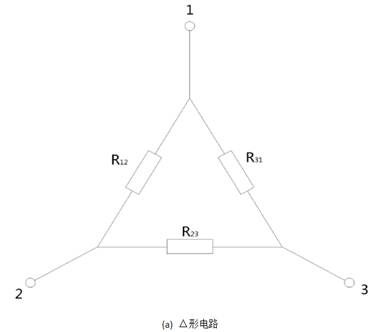
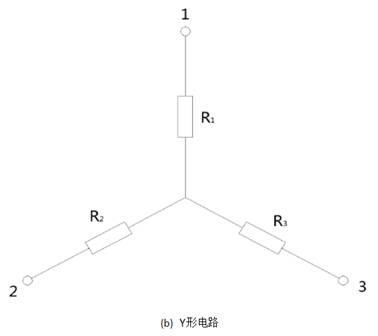
△形电路变换成Y形电路的方法为:
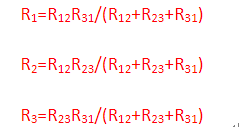
Y形电路变换成△形电路的方法为:

再回到电桥电路中:

把R10、R3、R4组成的Y形电路转化为△形电路,
R3_10=R3+R10+R3*R10/R4=2+2+4/2=6K。
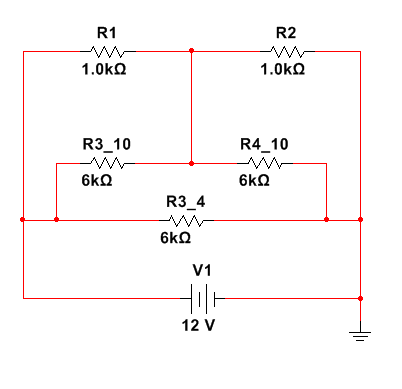
此时电路就简单了。
R等效=((R1//R3_10)+(R2//R4_10))//R3_4=1.333K。
二端网络的等效分析
任何一个有源线性二端网络,对外电路来说,都可以用一个等效电压源来代替。等效电压源的源电压等于有源二端网络的开路电压。等效内阻等于有源二端网络所有电源作用等于零(理想电压源短接,其源电压为零;理想电流源开路,其源电流为零)后所得无源二端网络a,b间的等效内阻,这就是戴维南定理。
任何一个有源线性二端网络,对外电路来说,都可以用一个等效电流源来代替。等效电流源的源电压等于有源二端网络的短路电流。等效内阻等于有源二端网络所有电源作用等于零(理想电压源短接,其源电压为零;理想电流源开路,其源电流为零)后所得无源二端网络a,b间的等效内阻,这就是诺顿定理。
-
电桥电路的常见错误分析2025-01-09 2044
-
微变等效电路用于分析什么2024-08-16 3065
-
微变等效电路和小信号等效电路分析方法的区别2024-07-16 3520
-
微变等效电路和小信号等效电路的区别2024-07-15 4086
-
诺顿等效电路和戴维南等效电路的区别2023-12-07 8751
-
含受控源电路的分析与等效计算2023-11-18 388
-
直流电桥的变形电路计算2023-03-10 2376
-
LLC电路等效分析总结2022-07-15 1138
-
电阻电路的等效变换及一般分析2022-03-24 925
-
第2章电路分析中的等效变换22017-03-01 1229
-
线性电路分析中受控电源的等效方法2016-03-04 970
-
关于电路的等效化简分析法2010-05-19 678
-
电阻电路的等效变换2009-07-08 765
-
交流等效电路分析法2008-11-08 20888
全部0条评论

快来发表一下你的评论吧 !

