1/4波长阻抗变换器

如同在上一篇文章中所说，阻抗匹配贯穿整个射频电路的设计，阻抗匹配的终极目标就是如何让电磁波能够更好的传播到负载，并且被负载全部吸收。阻抗匹配有很多方法，我们今天仅列举几种最常用的方法。   负载阻抗匹配就是在传输线和负载之间加入一个阻抗匹配网络，阻抗匹配网络应该全部由无耗元件组成，其匹配原理就是通过阻抗匹配网络引入一个新的反射波，这个反射波与负载因其的反射波等辐反相，相互抵消，使传输线上没有反射波，从而实现行波工作状态。从阻抗的角度来说，阻抗匹配是用一个新的网络将原来不等于传输线特性阻抗的负载阻抗变换成为等于传输线特性阻抗的阻抗。如下图所示：

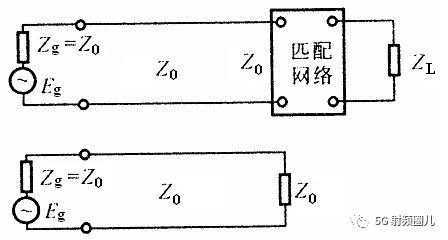
常用的阻抗匹配方法很多，我们今天一起来学习下四分之一阻抗变换器匹配的原理。  

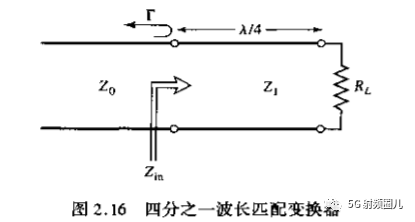
四分之一波长阻抗变换器是有一段长度为lambda0/4，阻抗为Z01的传输线构成，其中Lambda0是传输线所传输信号的中心频率所对应的相波长，与信号频率f0，传输线的结构，填充介质等因素有关。当传输线的终端接纯电阻负载RL时，在中心频率上的输入阻抗为：

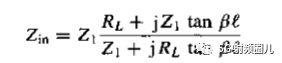
为了计算该式在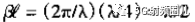时的值，我们可以用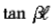去除上式的分子分母，并取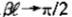的极限，即可得：

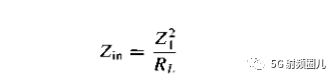
为了使反射系数等于0，必须有Z0=Zin，可得四分之一波长变换器的特性阻抗为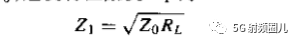： 可以看出了，这个阻抗就是负载阻抗和传输线阻抗的几何平均。因此在传输线上就没有驻波，反射系数为0，但是在四分之一阻抗变换器内还是有驻波存在。变换器上的驻波系数为：

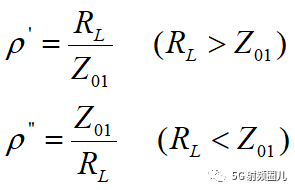
注意：上式是基于信号的中心频率f0来求解的，因此只能在这个点上实现匹配，或者匹配线的长度是该频率的四分之一波长或者四分之一波长的奇数倍（2n+1）处实现完全匹配，在其他频率上将会失配。

上式只能用于实阻抗匹配，即负载的阻抗为纯电阻。但是对于一般的复阻抗负载，ZL=RL+jXL，时，一般先经过一个适当长度的传输线把负载阻抗变换为实阻抗负载。下面介绍两种常用的匹配方法：
方法一：终端接四分之一波长阻抗变换器的同时，并联一段特性阻抗为Z0，长度为s的终端段路线。
 

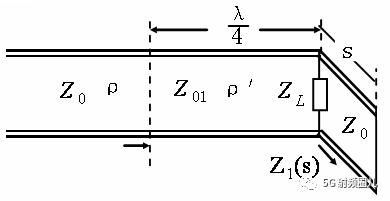
终端短路线在负载处提供一个纯电抗，只要选择合适的长度s，就可以使其在负载处所呈现的电抗来抵消负载的电抗部分，从而使负载的总阻抗为实数，然后利用四分之一波长阻抗变换器将负载处的等效阻抗变换为Z0，实现阻抗匹配。
方法二：在靠近终端的电压波腹点或者波节点处接入四分之一波长阻抗变换器来实现复阻抗匹配。

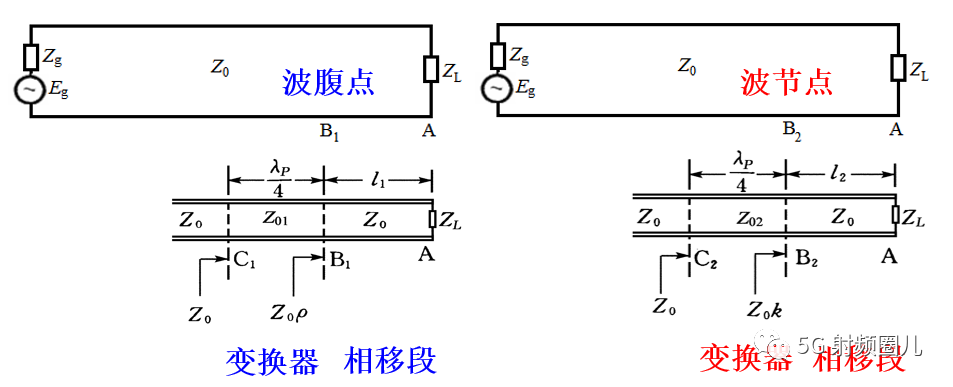
传输线上电压波节点或者波腹点的阻抗为实数，所以如果在这两个位置剪短传输线，接入特性阻抗为Z01的四分之一波长变换器就可以进行阻抗匹配。负载与电压波节点或者波腹点位置的传输线称为相移段。
1，当电压波腹点接入四分之一波长变换器时，相移段长度L和变换器特性阻抗分别为：

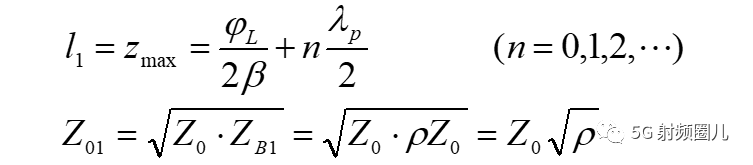
2，当电压波节点接入四分之一波长变换器时，相移段长度L和变换器特性阻抗分别为：

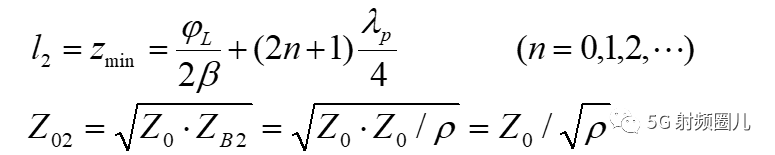
这个时候阻抗变换器上的驻波系数为：

为了更深入的了解四分之一波长阻抗变换器的特性，我们一起来看一下多次反射的概念。
 

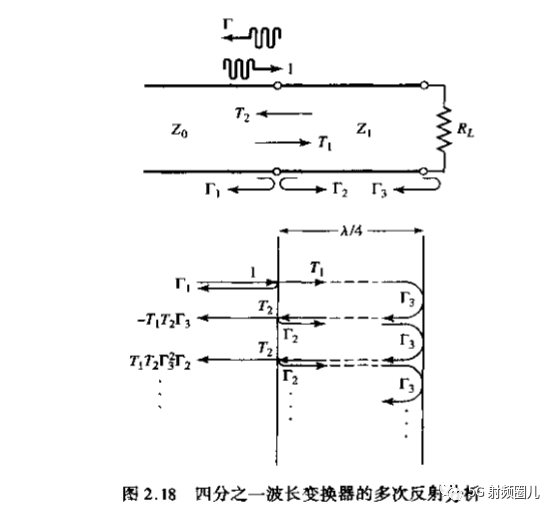
对于上图给出的四分之一波长变换器，它具有一下的反射系数：

这些反射系数可以表示为：

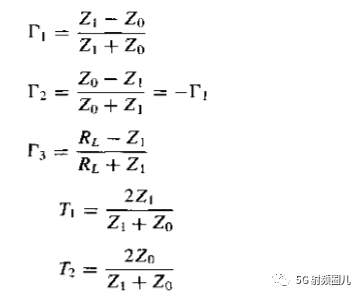
我们可以想象一下，当电磁波信号沿着传输线进入四分之一波长变换器时，它首先看到的阻抗是Z1，因为还没有到达负载RL，因而负载还看不到它的影响。一部分电磁波被反射，另一部分被传输进入四分之一波长变换器，然后被传输的电磁波到达负载时遇到了组在阻抗RL，再次被反射，经过四分之一波长到达传输线和变换器的交界处，遇到阻抗Z0，再次被反射回到负载，电磁波在变换器内不断额被反射吸收，每次反射波都要经过往返两次四分之一波长，产生相位差180°，总的反射系数就是这无数次反射系数的和：

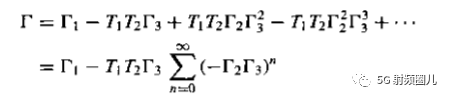
经过一系列的计算：

我们发现，当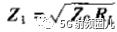时，上式为0，那么总的反射系数也为0，传输线是匹配的。
那么我们发现四分之一波长变换器匹配的原理就是通过选择恰当的匹配段的特性阻抗，和长度，使得所有的部分反射的结果叠加为0，来消除组播，形成整个传输线上的行波。可见变换器内部的斗争还是蛮激烈的。

审核编辑 ：李倩