坐标转换与参数计算介绍

大地坐标系之间的转换一直是导航领域十分关注的课题，在GPS的应用中有着必不可少的作用。 随着GPS越来越广泛的使用，其精度要求也越来越高，大地坐标系之间的转换的重要性日趋明显，甚至许多项目的成败完全取决于坐标系统的转换和转换精度。 随着计算机技术及移动互联网的飞速发展，数据的处理和信息的传递突破了时间和地域的限制，作为信息时代的产物和宠儿，全球定位系统得到了空前的发展和应用，为空间定位提供了准确、可靠的数据，而这些准确、可靠的数据更需要算法的支持。 在手机软件测量大师的开发过程中，我有幸涉猎到该领域的算法知识。 在这里我将分别从坐标系统基本理论、不同坐标系及不同椭球间的坐标转换、测量大师中的坐标转换方法及参数计算过程这几个方面来进行简单介绍。

一坐标系统基本理论

1、地球椭球的基本概念

在测量学中，把用来表示地球的椭球称为地球椭球，它是地球的数学表示，是经过一定选择的旋转椭球。 参考椭球是具有一定的几何参数、定位以及定向的用来表示某一大地面的地球椭球。 各个国家根据局部的天文、大地和重力的测量资料，研究当地大地水准面的情况，确定一个与地球椭球接近的椭球，用来表示地球的参考形状及大小，以此作为处理大地测量成果的依据，一般称这个椭球的外表面为参考椭球面。 参考椭球只能较好的接近大地水准面，并不能反映大地体的一切情况。

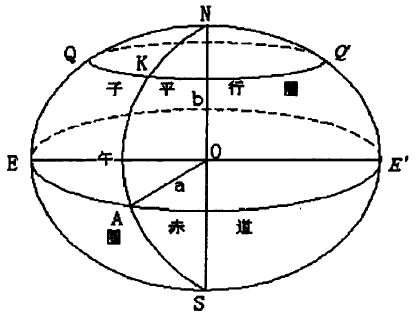
图1 参考椭球

旋转椭球是某椭圆绕其自身短轴旋转而成的几何形体。 子午椭圆的五个基本元素分别为:长半轴a、短半轴b、扁率f、椭圆第一偏心率e、椭圆第二偏心率e\'。 这其中，a, b为长度元素，f体现了椭球的扁平程度。 e和e\'为椭圆的焦点偏离中心的距离与其半径的比值。 要确定旋转椭球的形状和大小，只要知道这五个基本参数中的一个长度元素和其他任意一个参数便足够了。 如图1所示，O为椭球中心，NS是旋转轴，a是长半轴，b是短半轴。 子午面是通过椭球旋转轴的平面，其与椭球面的交线叫做子午圈； 平行圈是椭球面与垂直于旋转轴的平面截得的圆，这其中经过椭球中心O的平行圈叫做赤道。

2、常用坐标表现形式

为了表示椭球面上点的位置，必须建立相应的坐标系，选用不同的坐标系，其坐标表现形式也不同。 椭球点上的位置，在大地测量学中通常采用的坐标系有大地坐标系，空间直角坐标系，平面直角坐标系等。 在同一参考椭球基准下，大地坐标系，空间直角坐标系，平面直角坐标系是等价的，是一一对应的，只是不同的坐标表现形式。

(1)大地坐标系

大地坐标系是大地测量的基本坐标系，是全世界公用的最方便的坐标系统，对于研究地球形状、编制地图和大地测量的计算等方面都有很大作用。 如图2所示在大地坐标系中，空间中任意点的位置采用大地纬度B、大地经度L和大地高H来表示。 大地纬度是指空间中某一点P的法线与赤道面的夹角，赤道以北叫做北纬； 赤道以南叫做南纬。 大地经度是指P点所在的子午面与参考椭球的起始子午面所构成的夹角，起始子午面以东叫做东经，起始子午面以西叫做西经。 大地高H即空间的点沿着参考椭球的法线方向到椭球面的距离，由椭球面起算，向外为正，向内为负。 它与正高H正和正常高H正常，存在以下关系: H=H正+N(大地水准面差距)

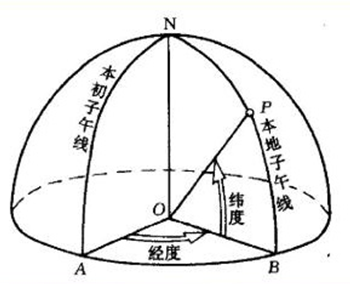
图2大地坐标系示意图

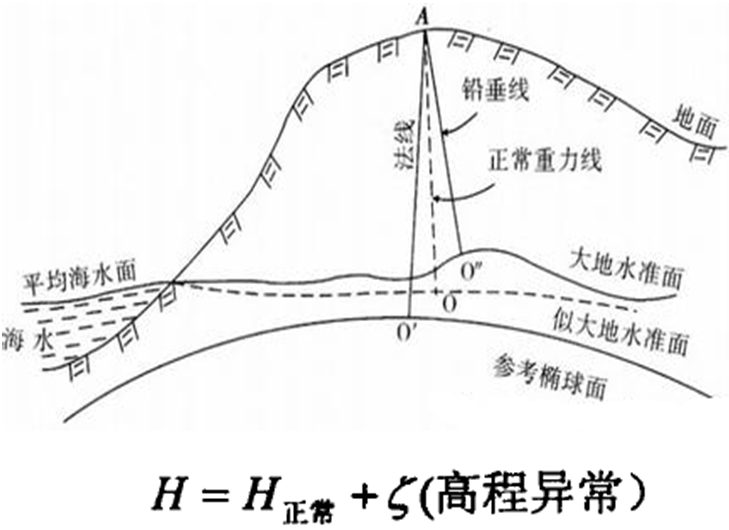
图3大地高程示意图

(2)空间直角坐标

空间直角坐标系的坐标原点为椭球的中心，X轴为赤道面和起始子午面的交线; 将在赤道面上并与X轴垂直的方向定为Y轴; 坐标系的Z轴为椭球的旋转轴，由此构成右手直角坐标系0-XYZ。

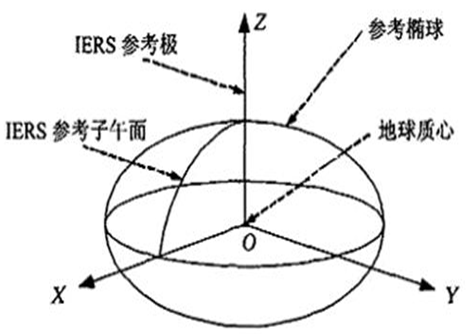
图4空间直角坐标系示意图

(3)平面直角坐标

在小范围内进行测量工作时如果用大地坐标来描绘点的空间位置是不适宜的，因此经常采用平面直角坐标。 测量学中的平面直角坐标系是利用某种投影变换例如高斯投影如图所示，将空间坐标经数学变换映射至平面上，投影变换的方法很多，我国通常采用高斯投影，因此在我国平面直角坐标系通常也称为高斯平面直角坐标系。 一般选择高斯投影平面作为坐标平面，与数学中的平面直角坐标系不同的是，其x轴为纵轴，上(北)为正，Y轴为横轴，右(东)为正，方位角是从北方向为准按顺时针方向计算出的夹角。

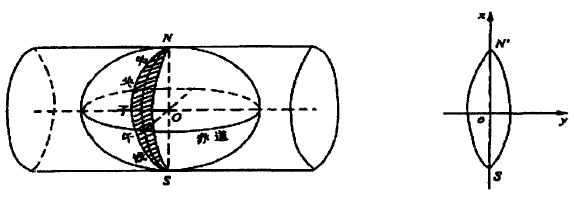
图5高斯投影平面直角坐标系

二不同坐标系及不同椭球间的坐标转换

测量坐标转换一般包括两方面的内容:坐标系转换和坐标基准转换。 同一坐标基准下，空间点不同表现形式的转换叫做坐标系转换。 如在WGS-84坐标系下，某点的大地坐标(B, L, H)与空间直角坐标(X,Y, Z)之间的转换。 坐标基准转换则为在不同坐标基准下的同一坐标表现形式的转换，必须求定两个不同坐标基准的转换参数才能进行转换。 如1954北京坐标系标系与2000国家大地坐标系下空间直角坐标的转换。 因此，从理论上讲，结合坐标系转换和坐标基准转换，便能在数据量足够多并精确的条件下，实现任意两个坐标基准之间不同坐标形式的转换。 具体流程如图6所示：

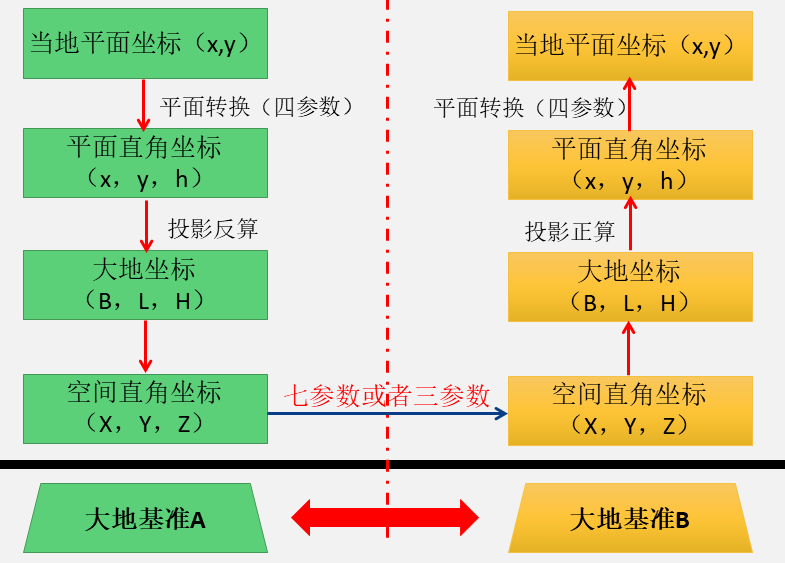
图6 坐标系转换及基准转换关系

我们都知道，在工程上使用的坐标主要是小区域范围的平面投影坐标，因此在接收机获取到WGS84的经纬度坐标时需要做进一步的坐标转换，我们测量大师已经满足需求。 这里介绍一下测量大师中涉及的坐标转换方法，其包括以下三种：四参数+高程拟合法（一步法）、七参数+四参数+高程拟合法（两步法）、七参数法。

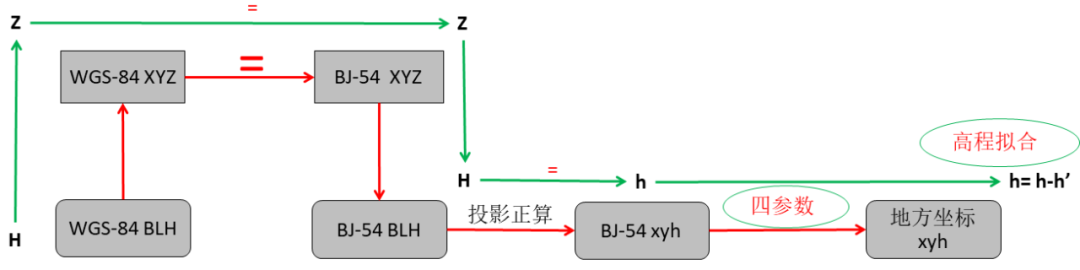
图7四参数+高程拟合

这里以WGS-84椭球下的坐标系转换到北京54椭球坐标系的过程为例来介绍这三种转换过程。 如图7所示，由接收机获取到的WGS-84的大地坐标（BLH）经过坐标系转换成WGS-84空间直角坐标系，然后直接赋值给北京54空间直角坐标系，在北京54椭球参数下进行空间直角坐标向大地坐标（BLH）转换，然后在进行高斯投影，从而获得平面直角坐标。 这里获取的投影坐标是有误差的，因此要通过提供四参数以及高程拟合参数分别对平面坐标及高程异常进行水平垂直矫正。

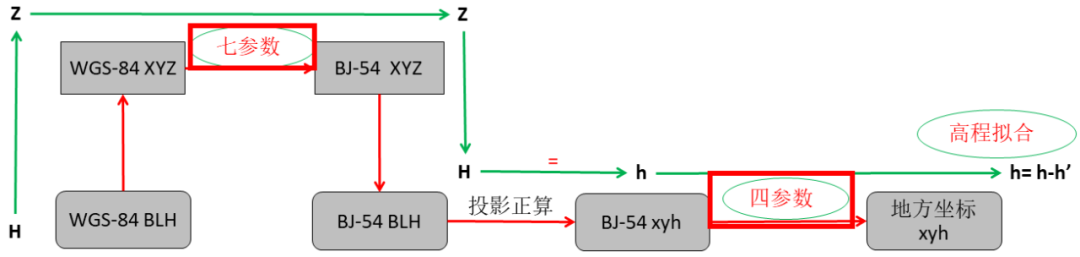
图8七参数+四参数+高程拟合

如图8所示，在WGS-84空间直角坐标向北京54空间直角坐标转换过程中需要已知的椭球间的转换七参数进行转换，然后在最后进行平面及高程矫正。 图9中，提供椭球间转换七参数即可，转换结果不进行矫正。

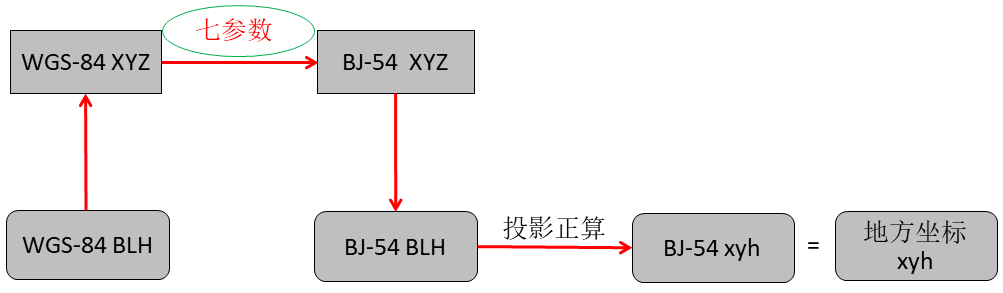
图9七参数法

三
参数计算过程

由前面可知，坐标转换过程中需要提供四参数、七参数以及高程拟合参数，那么这些参数是怎么得到的呢？ 这节就开始解密参数的计算过程。

在使用测量大师做参数计算时，当选择四参数+高程拟合参数的方法时，四参数及高程拟合参数计算如图10所示。 首先要有至少两组GNSS坐标和已知控制点坐标； ①先按照红色箭头的流程进行坐标转换，当转换到北京54平面投影坐标时，开始根据转换得到的坐标和已知的控制点平面坐标进行计算四参数。 ②再按照绿色箭头流程进行高程传递，根据转换得到的高和已知高计算出高程异常值，最后根据高程拟合算法进行计算拟合参数。 其中这里的高程拟合方法包括：加权平均值法、平面拟合法、曲面拟合法、带状拟合法。

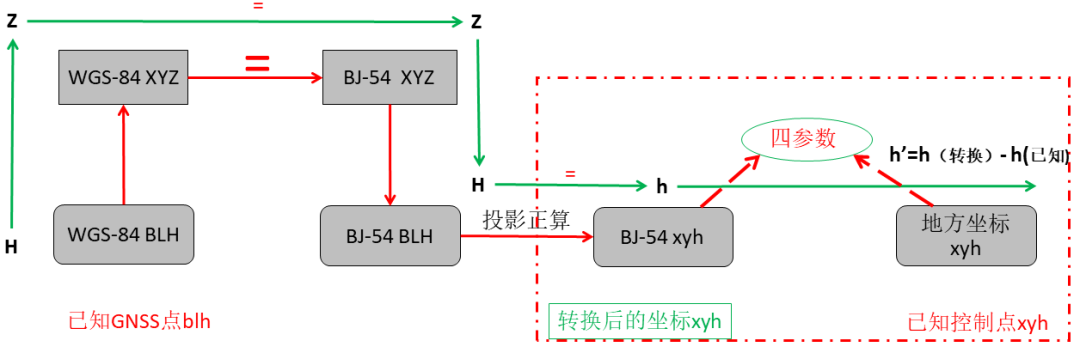
图10 四参数+高程拟合计算图解

当选择七参数+四参数+高程拟合参数法时，算法流程如图11所示：首先要确保至少三组GNSS坐标和已知控制点坐标； ①先按照红色箭头流程，左侧WGS-84大地坐标转换成WGS-84空间直角坐标，右侧由地方控制点坐标直接通过逆投影转换成北京54大地坐标，然后再转成北京54空间直角坐标，最后通过至少三组WGS-84空间直角坐标和北京54空间直角坐标计算出七参数； ②再按照绿色箭头流程，将已知GNSS坐标转换成WGS-84空间直角坐标，再使用①流程计算出的七参数进行基准转换成北京54空间直角坐标，并进一步转换成北京54平面坐标，从而与地方平面坐标进行对比计算出四参数； ③最后按照蓝色箭头流程通过七参数和四参数进行坐标转换，计算出高程异常值，进行高程拟合从而得到高程拟合参数。

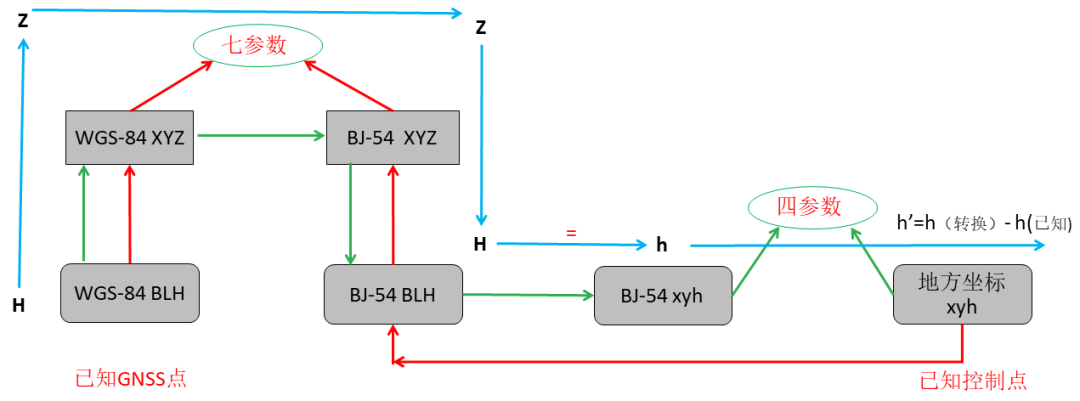
图11七参数+四参数+高程拟合计算图解

四成果展示

测量大师参数计算升级版本已经发布，这里展示一下我们的成果。 参数计算方法已实现四参数+高程拟合法、七参数+四参数+高程拟合法、七参数法如图12所示，高程拟合方法已实现加权平均法、平面拟合法、曲面拟合法、带状拟合法以及保留上一版本的垂直平差法如图13所示。 由图14、15、16可以看出我们的软件计算精度比肩同行软件，已经满足工程需求及市场需求。

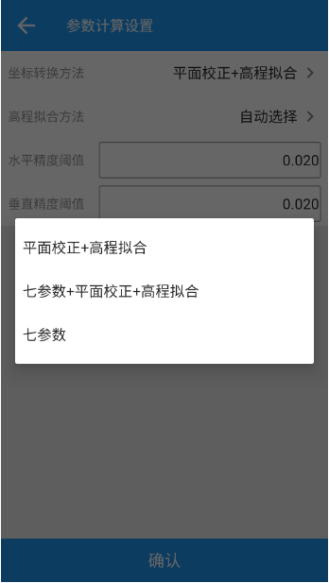
图12坐标转换方法

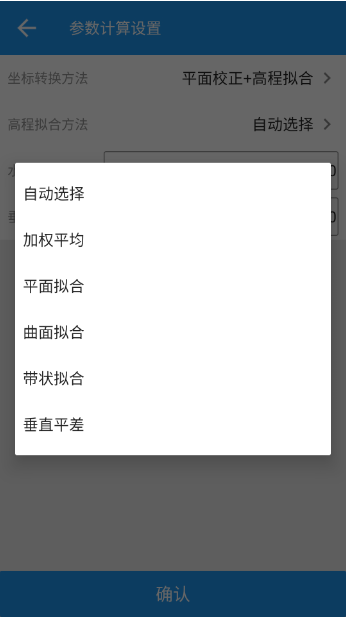
图13高程拟合方法

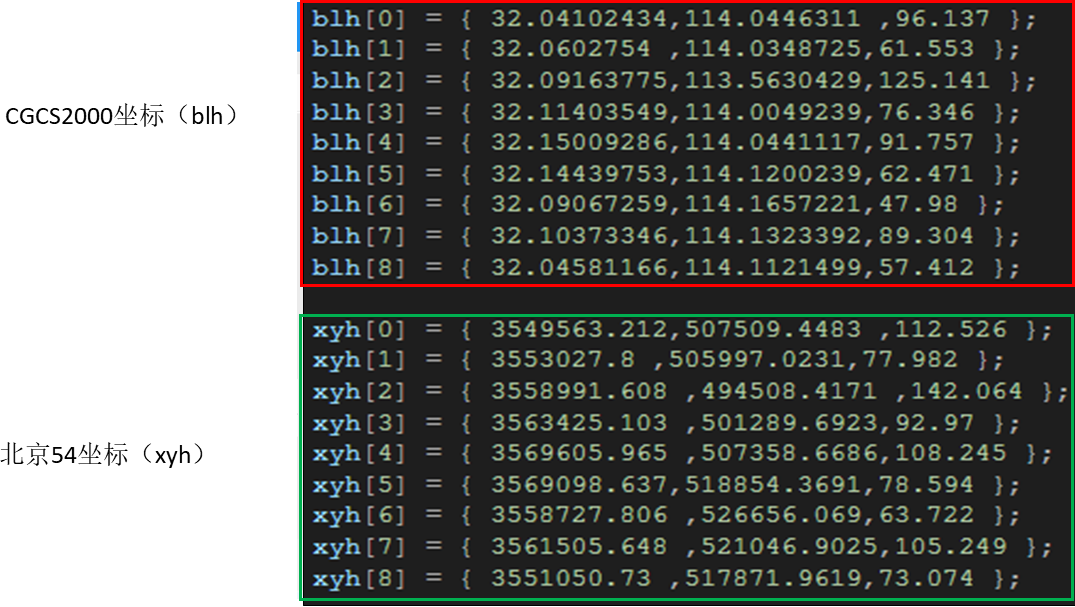
图14 实验数据

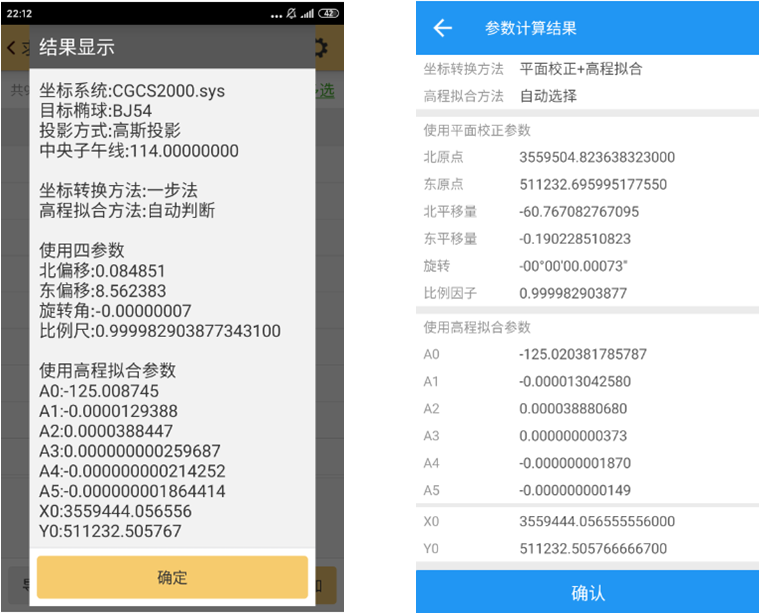
图15四参数+高程拟合法

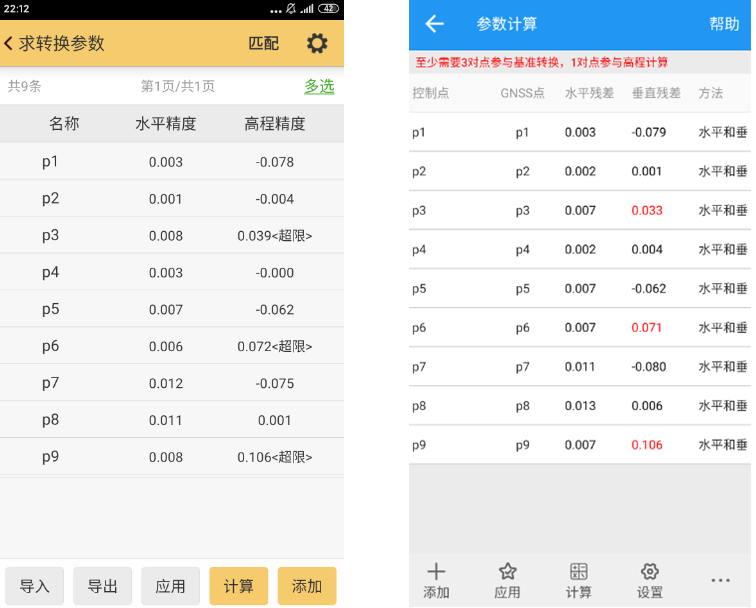
图16四参数+高程拟合法

审核编辑：汤梓红