科学设计锂电电极的客观规律介绍

改变电极的孔隙率和活性物质的负载量，同时采用放电试验对参数进行优化和验证，可以实现锂离子电池能量密度的最大化，从而优化基于物理学的电池多尺度模型。

尽管，电极和活性物质颗粒尺度对能量传输有一定损耗，但电极的最优尺度与其小尺度特性并无关系。电极的特性，如曲率、电解质浓度和锂离子扩散系数，都会影响电极的最佳尺度设计。

可以对其间的相关性进行归纳总结为一种普适性的关系：

孔隙率ε=0.13 log10(kεGrτ/(FDoc0)) 

面密度Qa= kQ/。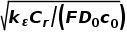

这一准则对电极结构的优化具有指导作用。  

【研究背景】

锂离子电池由于其能量密度高、功率密度大以及很好的循环寿命，已被广泛地应用在不同的领域。特别是电动汽车，其对锂离子电池提出了更高能量密度、低生产成本和长行驶里程的要求。传输阻抗对提高锂离子电池的能量密度至关重要。

离子传输阻抗可能在多孔电池电极内的不同长度尺度上发生，例如LixNi1/3Mn1/3Co1/3O2 (NMC111)电极 （如图1）。在电池运行充放电过程中，电解液中的锂离子扩散不仅要通过多孔电极，而且需要通过由晶体形成的二次聚合物。同时，嵌入的锂还必须从晶体的表面扩散到晶体内部。很难确定这两种离子传输类型中哪一种对电池的影响更大。

因此，通过在电极尺度获得最小的离子迁移阻抗，从而设计最优的电池电极，可能是一种提高电池能量密度更为直接、有效的方法。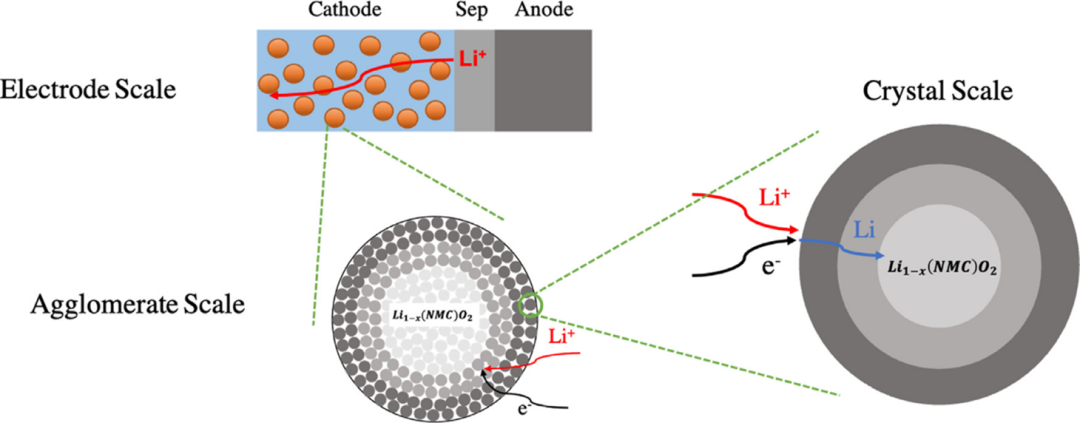



图 1. 锂离子在不同长度NMC111电极上的传输示意图。  

基于此，哥伦比亚大学的Alan C. West教授等人，建立了一个物理实验模型，并用实验结果对其进行验证。随后，使用验证后的物理模型对电池电极进行参数优化，并证实了锂离子在聚合物和晶体上的传输特性对电极优化参数没有影响。最后，证实了最优的电极设计参数确实具有普适性的关系。

必须指出的是，虽然电池循环稳定性因素在该项研究没有考虑，但其在后续研究中，能否获得电池的性能衰减机理是至关重要的。  

【研究理论与方法】

如图2a，在一定的电流下为了获得最大的电池体积能量密度，两个方面的因素需要考虑：当增加活性物质负载量或降低电极孔隙率时，电池体积会减小，从而提高电池的体积能量密度，但其降低离子的传输速率，反而导致低的电极材料利用率。

相反地，使用薄且多孔的电极有利于提高电极的利用率，但由于集流体和电池隔膜的厚度是一定的，此种设计方法也会导致体积能量密度的降低，因电池绝大部分的体积被惰性成分占据。

因此，在提高电极利用率和增加活性物质负载量之间，找到一个合适的平衡比例对优化电池的体积能量密度是非常关键的。

 

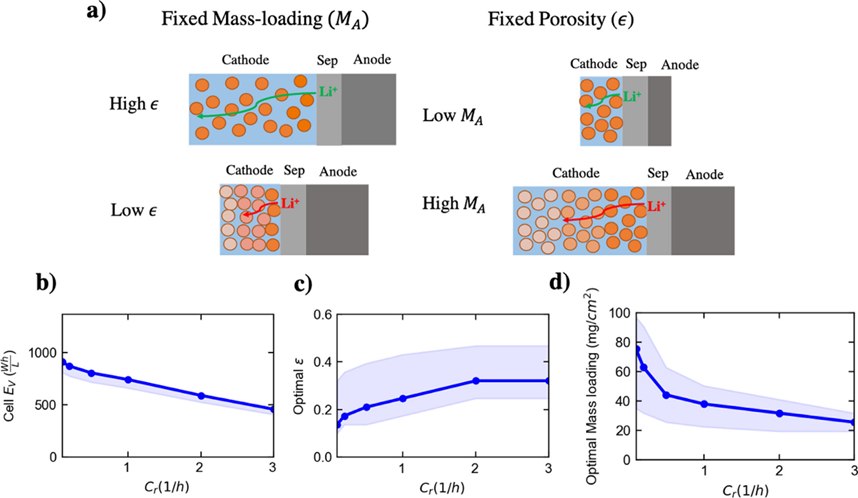
图 2. (a) 电极关键设计参数、活性物质负载量和孔隙率的示意图。(b) 不同放电倍率下的最优体积能量密度。(c-d) 获得最高体积能量密度时的最优电极孔隙率和负载量。  

如图2b-d所示，以LixNi1/3Co1/3O2(NMC111)为例，除了活性物质外，电极中还含有其他惰性物质，如粘结剂等。此类物质并不具有储锂能力，对电池能量没有贡献，因此，在保证电极稳定的机械性能的前提下，应尽可能地使活性物质的比例最大化，例如粘结剂等惰性物质的体积分数应略大于渗流阈值。另外，尽管电极的电子电导率是有限的，但对于所有的电池来说，电导率越大，电阻越小，电池性能越好。

因此，最佳的电极设计主要取决于电极的孔隙率（电导率决定性因素）和活性物质的负载量。图2b给出了体积能量密度与电流之间的关系，其对应的最佳负载量和电极孔隙率如图2c和2b所示。从图中可以得出，如果要获得一个在电流为1/h下工作的NMC111电极，当孔隙率为0.26且负载量为38 mg/cm2时，电池的体积能量密度最大。

由于增加孔隙率和惰性成分比例，或增加孔隙率、减小负载量，会降低电池的体积能量密度，而由于材料利用率低（每克活性物质所放出的电量），即使降低孔隙率或增加负载量，也会导致电池体积能量密度的降低。图2c显示，最佳活性物质负载量随电流增加而降低，表明电极在具有更高的孔隙率的同时也应该更薄，才能保持活性物质良好的利用率。  

【实验结果】

图3给出了最优体积能量密度、最佳ε值和负载量与团聚尺寸和扩散系数的函数关系：最优体积能量密度随着扩散系数的增加或者团聚尺寸的减少而增加。团聚尺寸对体积能量密度的影响，比扩散系数的影响更大。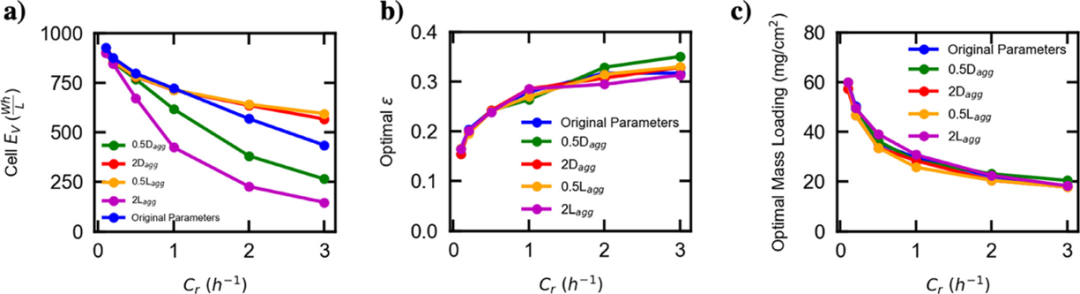



图 3.(a)最优体积能量密度与不同活性物质团聚尺寸和扩散系数的关系。(b-c) 最佳ε值和负载量与团聚尺寸和扩散系数的函数关系。  

图4a, 4c表明最佳孔隙率与负载量遵循Bruggeman关系。

在极端情况下，曲率度是所有孔隙度的总和。随着曲率的增加，电解质的有效扩散系数降低，这会导致更大的最佳孔隙率和更低的最佳负载量，从而保证了良好的电极利用率。图4b, 4d表明当电流放大τ倍时，最佳ε值和负载量与电流呈线性关系。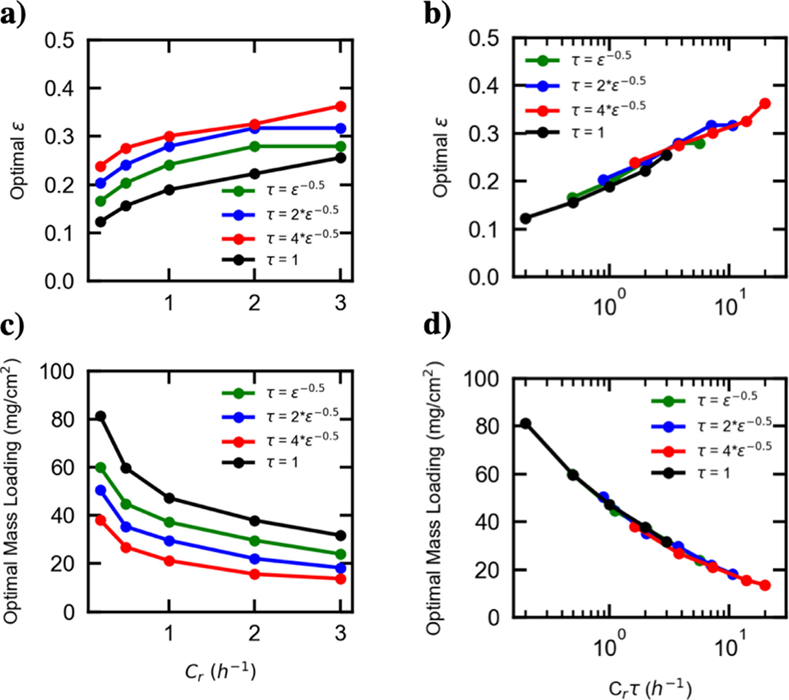



图 4. (a, c)最优电极参数与电极曲率的关系。(b, d) 最佳ε和负载量与电流放大倍数的关系。  

图5a, 5c 表明降低电解质扩散系数或电解液浓度，会导致最佳孔隙率的增加或最优负载量的降低。

图5b, 5d显示出Cr与1/(FDoc0)之间的关系。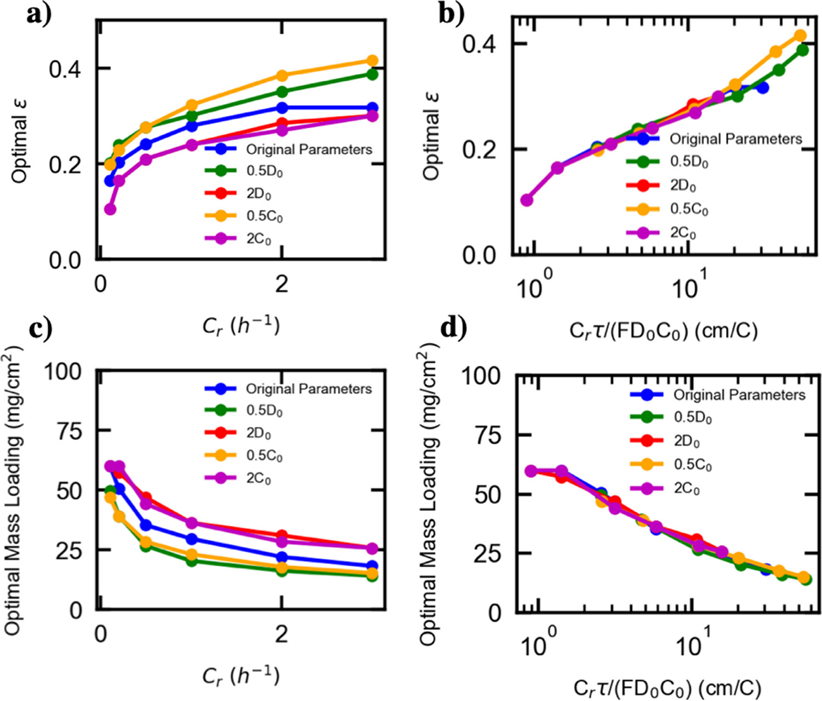



图 5. 最佳电极参数与电解质之间的关系，(a, c) 最佳参数与电解液扩散系数和浓度， (b, d) 最佳ε值和负载量与Grτ/(FDoc0)之间的关系。  

【实验讨论】

研究人员将提出的电极普适性设计原则应用到NMC、LVO、FEO和VOPO4四种不同的电极材料设计上，如图6所示。根据优化设计的结果显示，图7显示，采用计算的最优参数可以获得95%的理论最大体积能量密度。表明，所提出设计原则具有普适性，并且与活性物质无关。图8表明所计算的最佳ε值与最佳容量负载值（虚线）与数值优化后的结果（实现）非常吻合。特别是在95%灵敏度条件下。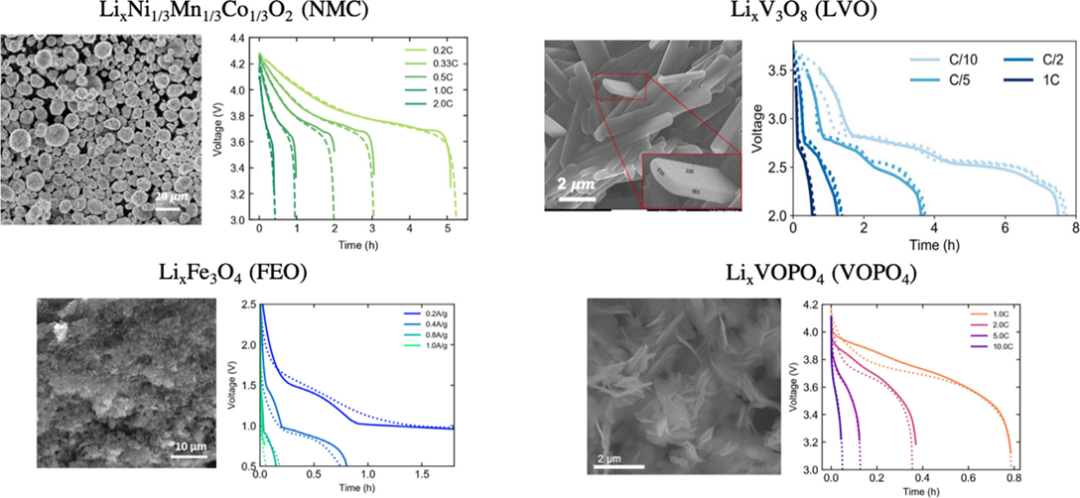



图 6. 不同电极材料的SEM图片和放电曲线。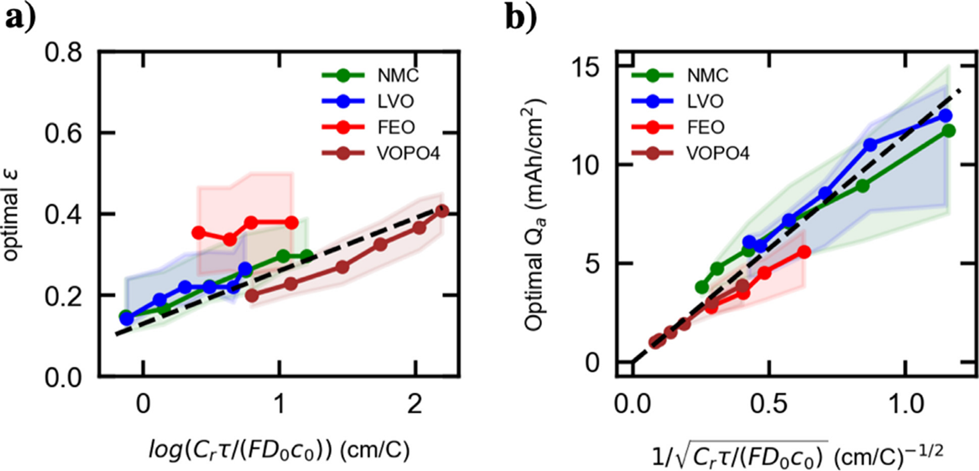



图 7. 对四种不同电极材料进行优化所获得的结果。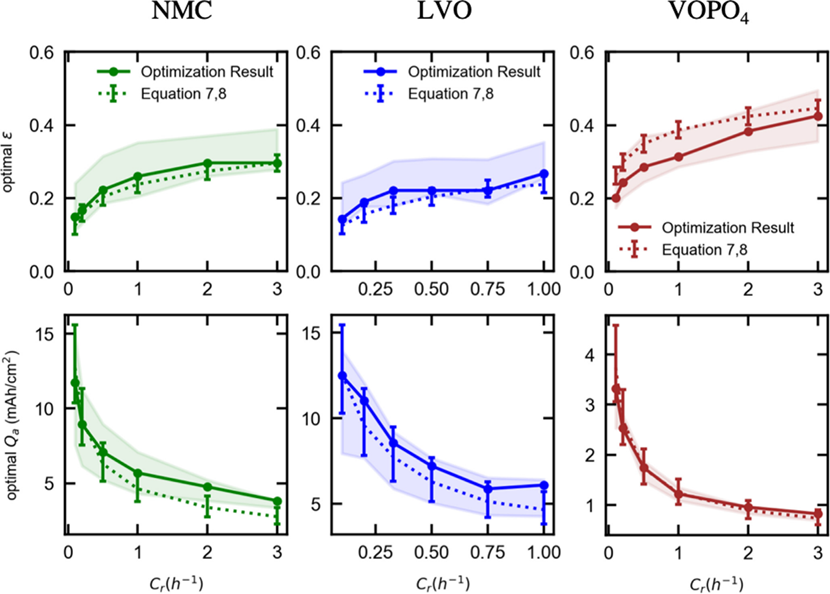



图 8.模拟的最优设计结果与Cr之间的函数关系。  

图9表明所提出的最佳负载量Qa与已报到的研究结果基本一致，即使控制参数稍有不同，也与报道的研究结果基本一致。并且所提出的普适性关系也适用于NMC622和LFP电极体系。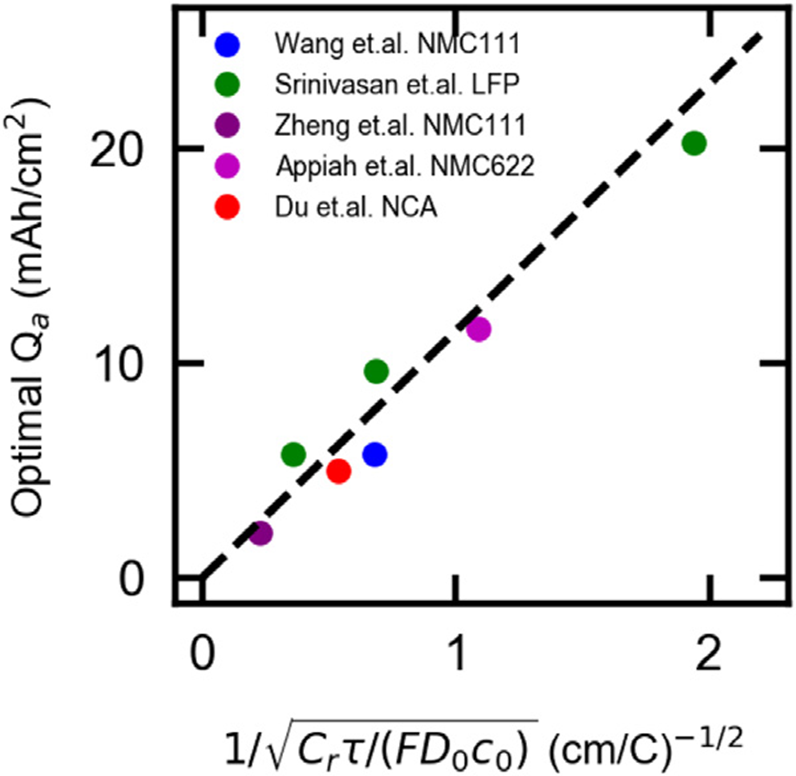



图 9. 最佳面积负载Qa的设计结果与其他研究结果的比较图。  

总之，虽然锂离子电池是一个非常复杂且多尺度的系统，其性能受不同尺度的离子传输阻抗的影响。该工作所开发的基于多尺度的物理模型，揭示了电池电极尺度离子传输的最优值与材料微观尺度上的独立性。

考虑到电解液的扩散率、浓度以及电极曲率，将广义电极优化应用于不同活性物质的锂电池电极，从而获得了电池性能与各个参数之间的普适性关系。

审核编辑：刘清