DepGraph：任意架构的结构化剪枝，CNN、Transformer、GNN等都适用！

1. 内容概要

本工作提出了一种非深度图算法DepGraph，实现了架构通用的结构化剪枝，适用于CNNs, Transformers, RNNs, GNNs等网络。该算法能够自动地分析复杂的结构耦合，从而正确地移除参数实现网络加速。基于DepGraph算法，我们开发了PyTorch结构化剪枝框架 Torch-Pruning。不同于依赖Masking实现的“模拟剪枝”，该框架能够实际地移除参数和通道，降低模型推理成本。在DepGraph的帮助下，研究者和工程师无需再与复杂的网络结构斗智斗勇，可以轻松完成复杂模型的一键剪枝。

论文标题：DepGraph: Towards Any Structural Pruning
论文链接：https://arxiv.org/abs/2301.12900
项目地址：https://github.com/VainF/Torch-Pruning

2. 背景介绍

结构化剪枝是一种重要的模型压缩算法，它通过移除神经网络中冗余的结构来减少参数量，从而降低模型推理的时间、空间代价。在过去几年中，结构化剪枝技术已经被广泛应用于各种神经网络的加速，覆盖了ResNet、VGG、Transformer等流行架构。然而，现有的剪枝技术依旧存在着一个棘手的问题，即算法实现和网络结构的强绑定，这导致我们需要为不同模型分别开发专用且复杂的剪枝程序。

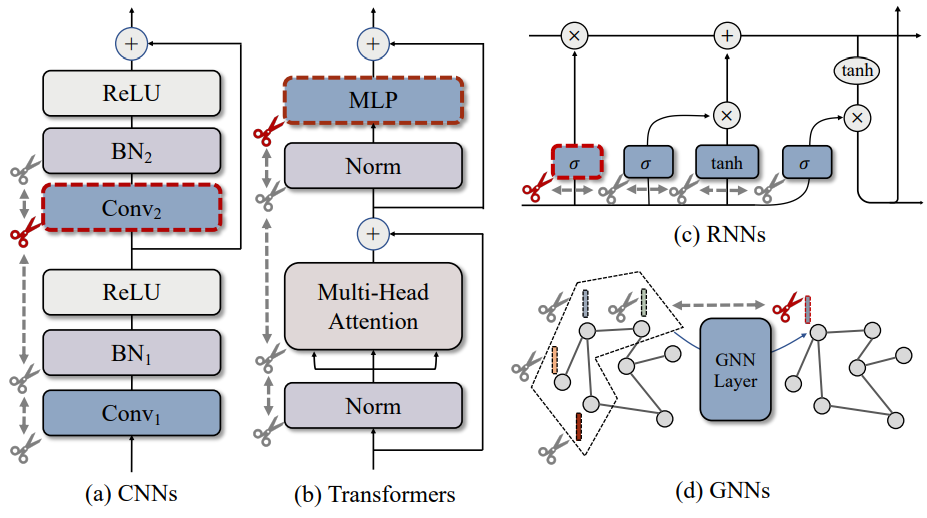
那么，这种强绑定从何而来？在一个网络中，每个神经元上通常会存在多个参数连接。如下图1（a）所示，当我们希望通过剪枝某个神经元（加粗高亮）实现加速时，与该神经元相连的多组参数需要被同步移除，这些参数就组成了结构化剪枝的最小单元，通常称为组（Group）。然而，在不同的网络架构中，参数的分组方式通常千差万别。图1（b）-（d）分别可视化了残差结构、拼接结构、以及降维度结构所致的参数分组情况，这些结构甚至可以互相嵌套，从而产生更加复杂的分组模式。因此，参数分组也是结构化剪枝算法落地的一个难题。

图1: 各种结构中的参数耦合，其中高亮的神经元和参数连接需要被同时剪枝

3. 本文方法

3.1 参数分组

未自动化参数分组，本文提出了一种名为DepGraph的（非深度）图算法，来对任意网络中的参数依赖关系进行建模。在结构化剪枝中，同一分组内的参数都是两两耦合的，当我们希望移除其中之一时，属于该组的参数都需要被移除，从而保证结构的正确性。理想情况下，我们能否直接地构建一个二进制的分组矩阵G来记录所有参数对之间耦合关系呢？如果第i层的参数和第j层参数相互耦合，我们就用来进行表示。如此，参数的分组就可以简单建模为一个查询问题：

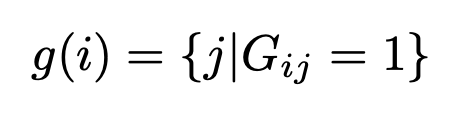
然而，参数之间是否相互依赖并不仅仅由自身决定，还会受到他们之间的中间层影响。然而，中间层的结构有无穷种可能，这就导致我们难以基于规则直接判断参数的耦合性。在分析参数依赖的过程中，我们发现一个重要的现象，即相邻层之间的依赖关系是可以递推的。举个例子，相邻的层A、B之间存在依赖，同时相邻的层B、C之间也存在依赖，那么我们就可以递推得到A和C之间也存在依赖关系，尽管A、C并不直接连接。这就引出了本文算法的核心，即“利用相邻层的局部依赖关系，递归地推导出我们需要的分组矩阵”。而这种相邻层间的局部依赖关系我们称之为依赖图（Dependency Graph），记作。依赖图是一张稀疏且局部的关系图，因为它仅对直接相连的层进行依赖建模。由此，分组问题可以简化成一个路径搜索问题，当依赖图中节点i和节点j之间存在一条路径时，我们可以得到，即i和j属于同一个分组。

3.2 依赖图建模

然而，当我们把这个简单的想法应用到实际的网络时，我们会发现一个新的问题。结构化剪枝中同一个层可能存在两种剪枝方式，即输入剪枝和输出剪枝。对于一个卷积层而言，我们可以对参数的不同维度进行独立的修剪，从而分别剪枝输入通道或者输出通道。然而，上述的依赖图却无法对这一现象进行建模。为此，我们提出了一种更细粒度的模型描述符，从逻辑上将每一层拆解成输入和输出。基于这一描述，一个简单的堆叠网络就可以描述为：

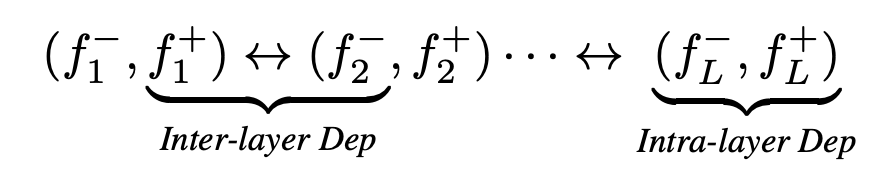
其中符号表示网络连接。还记得依赖图是对什么关系进行建模么？答案是相邻层的局部依赖关系！在新的模型描述方式中，“相邻层”的定义更加广泛，我们把同一层的输入和输出也视作相邻。尽管一个神经网络通畅包含了各种各样的层和算子，我们依旧从上式中抽象出两类基本依赖关系，即层间依赖（Inter-layer Dependency）和层内依赖（Intra-layer Dependency）。

层间依赖：首先我们考虑层间依赖，这种依赖关系由层和层直接的连接导致，是层类型无关的。由于一个层的输出和下一层的输入对应的是同一个中间特征（Feature），这就导致两者需要被同时剪枝。例如在通道剪枝中，“某一层的的输出通道剪枝”和“相邻后续层的输入通道剪枝”是等价的。

层内依赖：其次我们对层内依赖进行分析，这种依赖关系与层本身的性质有关。在神经网络中，我们可以把各种层分为两类：第一类层的输入输出可以独立地进行剪枝，分别拥有不同的剪枝布局（pruning shcme），记作或者。例如对于全连接层的2D参数矩阵，我们可以得到和两种不同的布局。这种情况下，输入和输出在依赖图中是相互独立、非耦合的；而另一类层输入输出之间存在耦合，例如逐元素运算、Batch Normalization等。他们的参数（如果有）仅有一种剪枝布局，且同时影响输入输出的维度。实际上，相比于复杂的参数分组模型，深度网络中的层类型是非常有限的，我们可以预先定义不同层的剪枝布局来确定图中的依赖关系。

综上所述，依赖图的构建可以基于两条简洁的规则实现，形式化描述为：

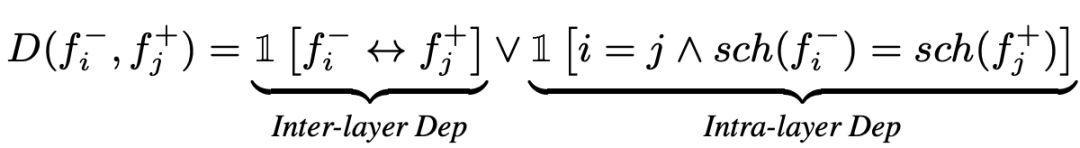
其中和分别表示逻辑”OR“和“AND”。我们在算法1和算法2中总结了依赖图构建和参数分组的过程，其中参数分组是一个递归的连通分量（Connected Component）搜索，可以通过简单深度或者宽度有限搜索实现。

将上述算法应用于一个具体的残差结构块，我们可以得到如下可视化结果。在具体剪枝时，我们以任意一个节点作为起始点，例如以作为起点，递归地搜索能够访问到的所有其他节点，并将它们归入同一个组进行剪枝。值得注意的是，卷积网络由于输入输出使用了不同的剪枝布局（），在深度图中其输入输出节点间不存在依赖。而其他层例如Batch Normalization则存在依赖。

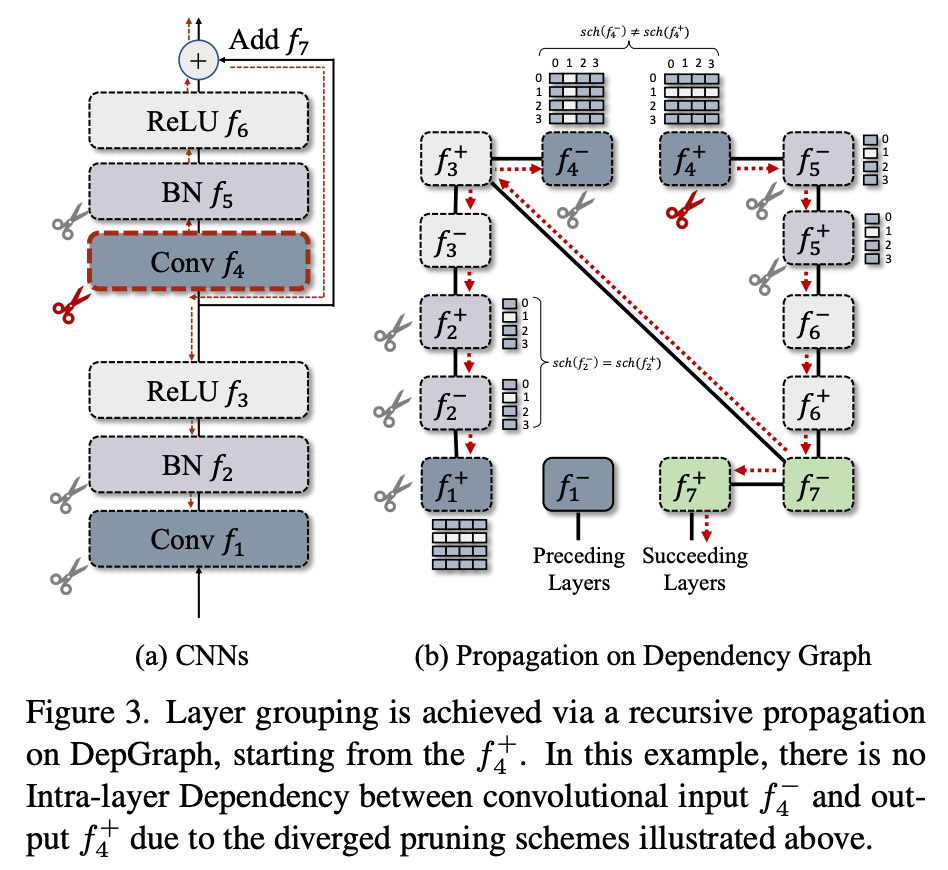
图2: 残差结构的依赖图建模

3.3 利用依赖图进行剪枝

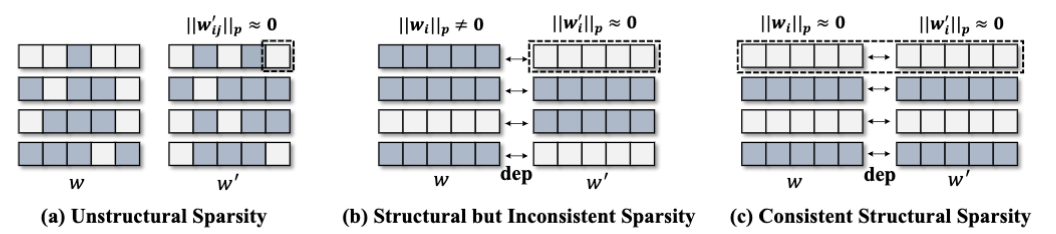
图3: 不同的稀疏性图示。本方法根据依赖关系对耦合参数进行同步稀疏，从而确保剪枝掉的参数是一致“冗余”的

依赖图的一个重要作用是参数自动分组，从而实现任意架构的模型剪枝。实际上，依赖图的自动分组能力还可以帮助设计组级别剪枝（Group-level Pruning）。在结构化剪枝中，属于同于组的参数会被同时移除，这一情况下我们需要保证这些被移除参数是“一致冗余”的。然而，一个常规训练的网络显然不能满足这一要求。这就需要我们引入稀疏学习方法来对参数进行稀疏化。这里同样存在一个问题，常规的逐层独立的稀疏技术实际上是无法实现这一目标，因为逐层算法并不考虑层间依赖关系，从而导致图2 (b)中非一致稀疏的情况。为了解决这一问题，我们按照依赖关系将参数进行打包，如图2 (c)所示，进行一致的稀疏训练（虚线框内参数被推向0），从而使得耦合的参数呈现一致的重要性。在具体技术上，我们采用了一个简单的L2正则项，通过赋予参数组的不同正则权重来进行组稀疏化。

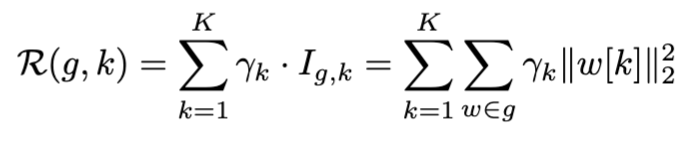
其中k用于可剪枝参数的切片（Slicing），用于定位当前参数内第k组参数子矩阵，上述稀疏算法会得到k组不同程度稀疏的耦合参数，我们选择整体L2 norm最小的耦合参数进行剪枝。实际上，依赖图还可以用于设计各种更强大的组剪枝方法，但由于稀疏训练、重要性评估等技术并非本文主要内容，这里也就不再赘述。

4 实验

4.1 Benchmark

本文实验主要包含两部分，第一部分对喜闻乐见的CIFAR数据集和ImageNet数据集进行测试，我们验证了多种模型的结构化剪枝效果，我们利用DepGraph和一致性稀疏构建了一个非常简单的剪枝器，能够在这两种数据集上取得不错的性能。

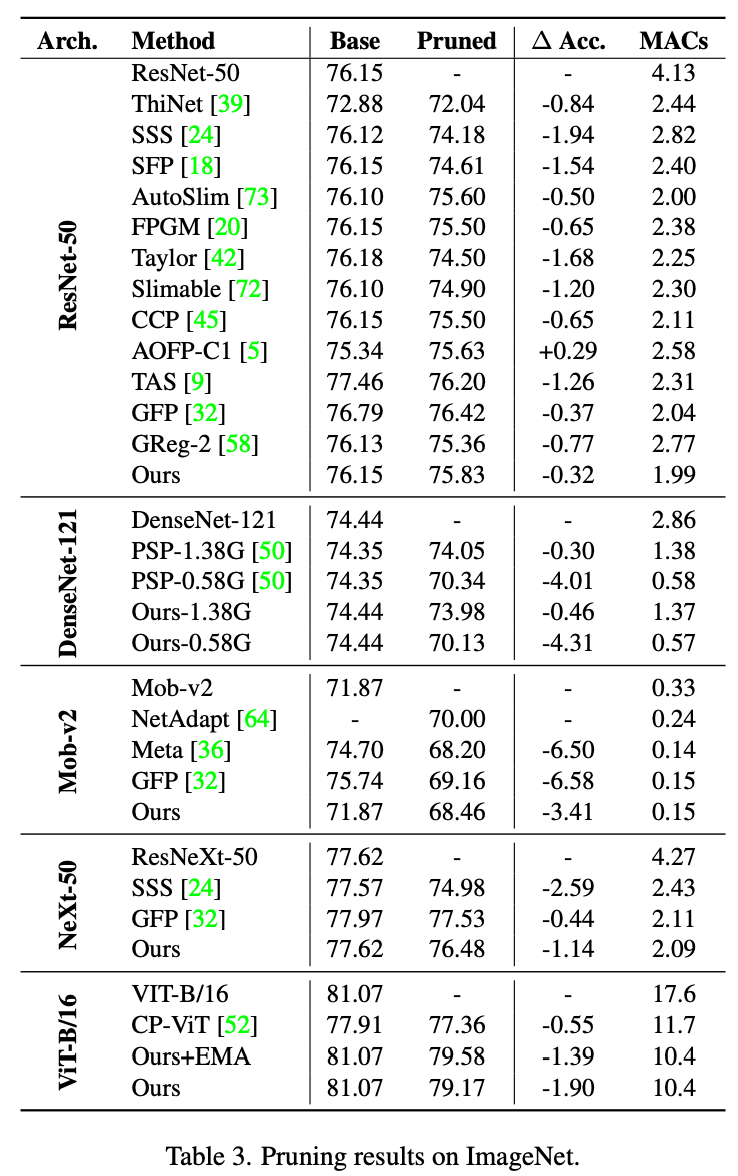
4.2 分析实验

一致性稀疏：在分析实验中，首先我们首先评估了一致性稀疏和逐层独立稀疏的差异，结论符合3.3中的分析，即逐层算法无法实现依赖参数的一致稀疏。例如下图中绿色的直方图表示传统的逐层稀疏策略，相比于本文提出的一致性稀疏，其整体稀疏性表现欠佳。

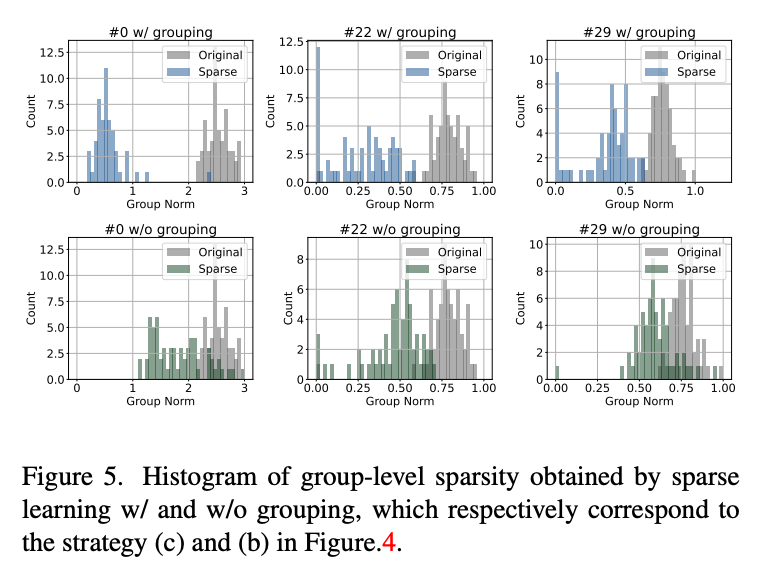
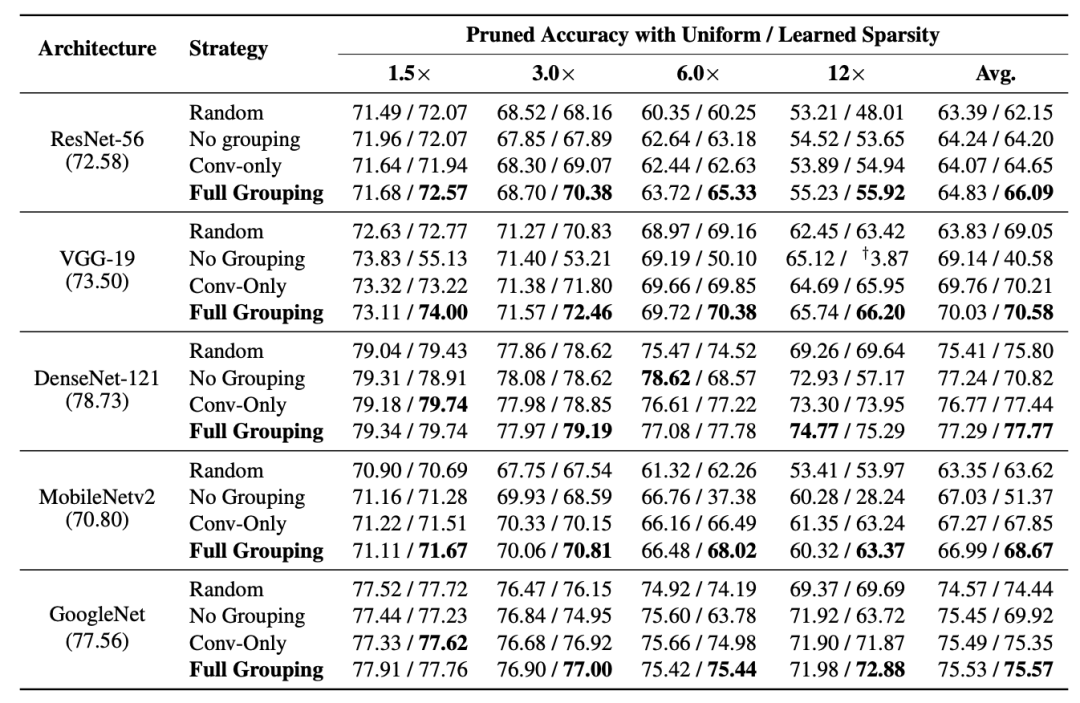
分组策略/稀疏度分配：我们同样对分组策略进行了评估，我们考虑了无分组（No Grouping）、卷积分组（Conv-only）和全分组（Full Grouping）三种策略，无分组对参数进行独立稀疏，卷积分组近考虑了卷积层而忽略其他参数化的层，最后的全分组将所有参数化的层进行一致性稀疏。实验表明全稀疏在得到更优的结果同时，剪枝的稳定性更高，不容易出现过度剪枝的情况（性能显著下降）。

另外剪枝的稀疏度如何分配也是一个重要问题，我们测试了算法在逐层相同稀疏度（Uniform Sparsity）和可学习稀疏度（Learned Sparsity）下的表现。可学习稀疏度根据稀疏后的参数L2 Norm进行全局排序，从而决定稀疏度，这一方法能够假设参数冗余并不是平均分布在所有层的，因此可以取得更好的性能。但于此同时，可学习的稀疏度存在过度剪枝风险，即在某一层中移除过多的参数。

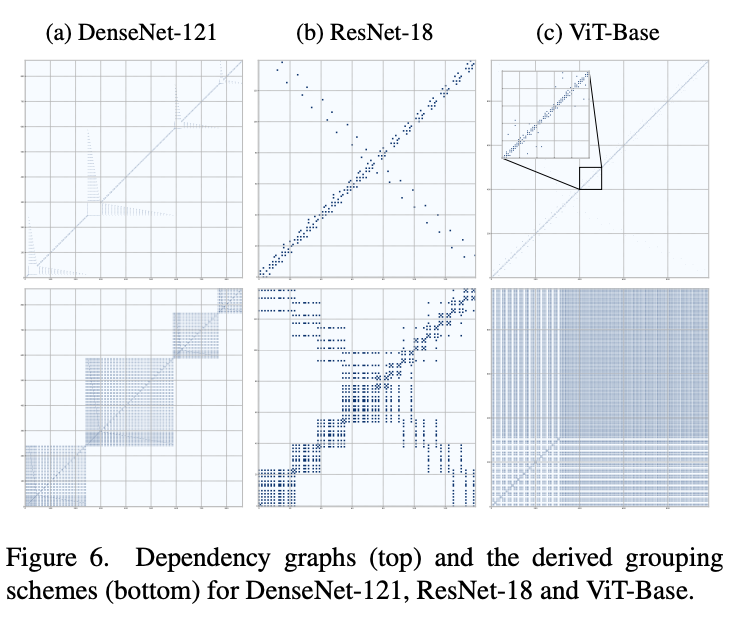
依赖图可视化：下图中我们可视化了DenseNet-121、ResNet-18、ViT-Base的依赖图和递归推导得到的分组矩阵，可以发现不同网络的参数依赖关系是复杂且各不相同的。

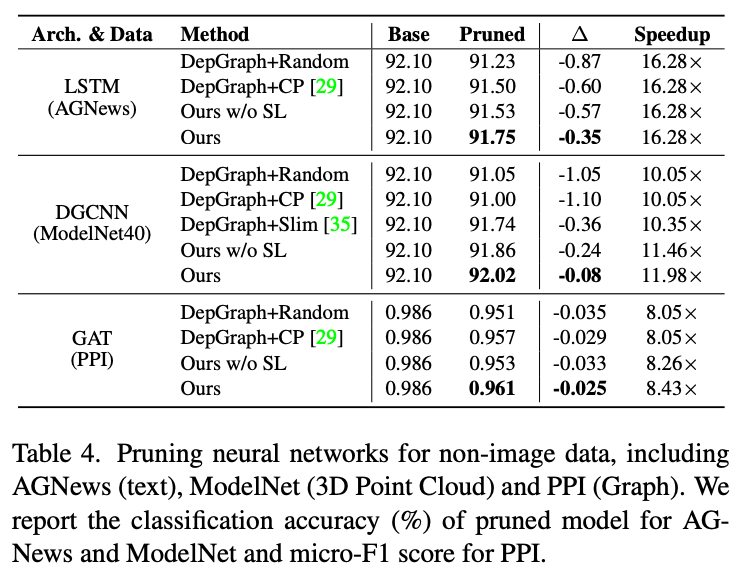
非图像模型结构化剪枝：深度模型不仅仅只有CNN和transformer，我们还对其他架构的深度模型进行了初步验证，包括用于文本分类的LSTM，用于3D点云分类的DGCNN以及用于图数据的GAT，我们的方法都取得了令人满意的结果。

5 Talk is Cheap

5.1 A Minimal Example

在本节中我们展示了DepGraph的一个最简例子。这里我们希望对一个标准ResNet-18的第一层进行通道剪枝：

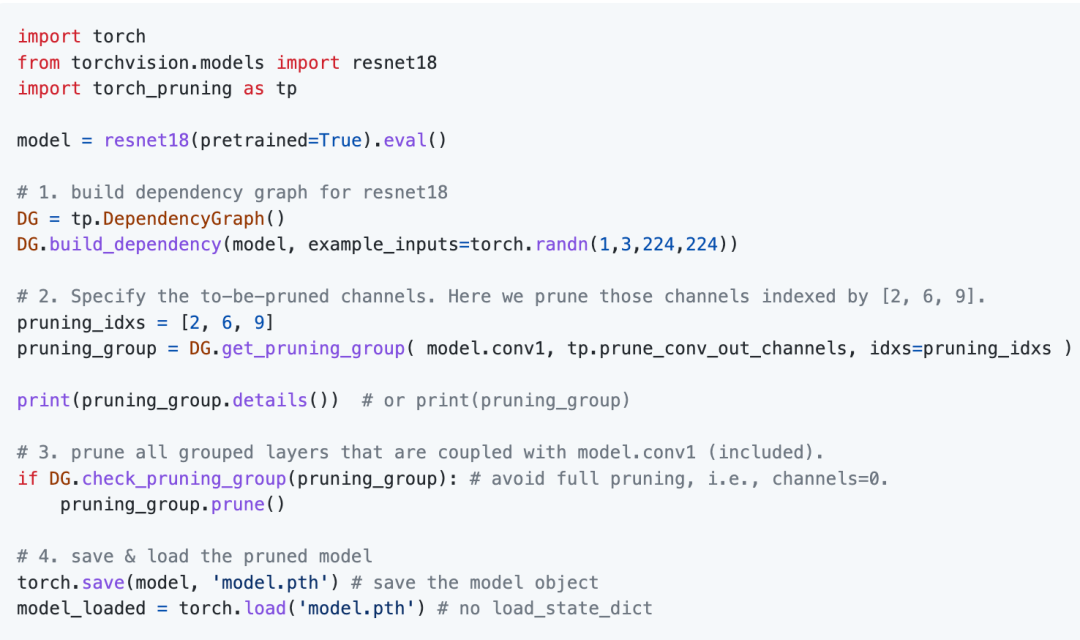
通过调用DG.get_pruning_group我们可以获取包含model.conv1的最小剪枝单位pruning_group，然后通过调用pruning_group.prune()来实现按组剪枝。通过打印这一分组，我们可以看到model.conv1上的简单操所导致的复杂耦合：

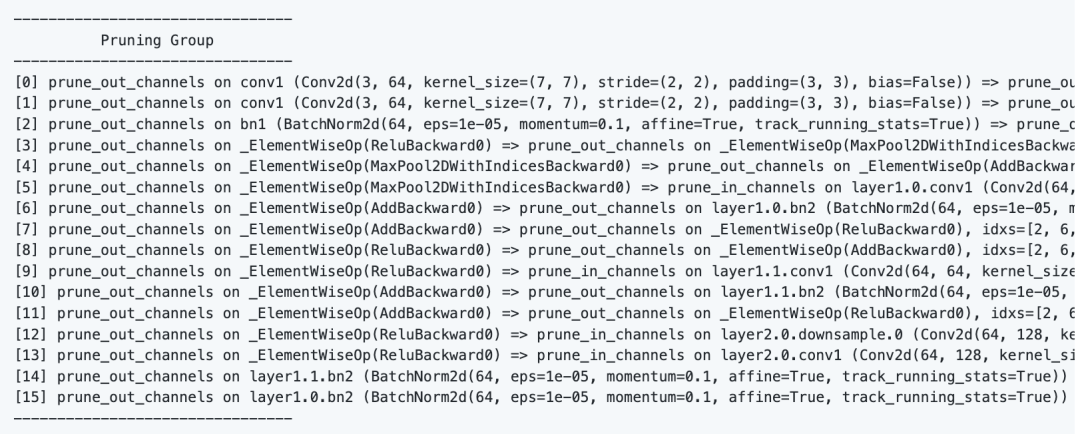
此时，如果不依赖DepGraph，我们则需要手动进行逐层修剪，然而这通常要求开发者对网络结构非常熟悉，同时需要手工对依赖进行分析实现分组。

5.2 High-level Pruners

基于DepGraph，我们在项目中支持了更简单的剪枝器，用于任意架构的一键剪枝，目前我们已经支持了常规的权重剪枝（MagnitudePruner）、BN剪枝（BNScalePruner）、本文使用的组剪枝（GroupNormPruner）、随机剪枝（RandomPruner）等。利用DepGraph，这些剪枝器可以快速应用到不同的模型，降低开发成本。

6 总结

本文提出了一种面向任意架构的结构化剪枝技术DepGraph，极大简化了剪枝的流程。目前，我们的框架已经覆盖了Torchvision模型库中85%的模型，涵盖分类、分割、检测等任务。总体而言，本文工作只能作为“任意结架构剪枝”这一问题的初步探索性工作，无论在工程上还是在算法设计上都存在很大的改进空间。此外，当前大多数剪枝算法都是针对单层设计的，我们的工作为将来“组级别剪枝”的研究提供了一些有用的基础资源。

审核编辑 ：李倩