电机绕组：分数槽绕组的循环数序和绕组构成

1 分数槽绕组的循环数序

1.1 什么是分数槽绕组的循环数序

利用槽电势星型图可以确定分数槽绕组每相所属的槽号及连接规律，检查绕组对称情况等。对于槽数比较少的分数槽电机，这种方法简便、易行、直观，特别是在微特电机中，常采用多极少槽q＜1的所谓“分数槽集中绕组”，最适合用槽电势星型图来进行分相和确定绕组连接关系。但当槽数很多时，画槽电势星型图就显得非常麻烦，例如一些大型的水轮发电机、直驱风力发电机等，它们的槽数动辄数百上千个槽，画槽电势星型图费时费力。其实将各槽分相的方法有很多，槽电势星型图法只是其中的一种，接下来我们就再介绍一种实践中常用的“循环数序”的分相方法。

分数槽绕组的每极每相槽数q为分数，意味着每相在每个极下分得的槽数不相等，主要表现为同一极下不同相所占的槽数不相等，有些相多一个槽，有些相少一个槽；同一相在不同极下分得的槽数也不一样，有些极下多一槽，有些极下少一槽。这两种体现方式归根结底就是相带大小不同，有些相带多一槽，我们称之为大相带；有些相带少一槽，我们称之为小相带。各相带沿定子整个圆周依次分得的槽数组成了一个数字序列，这一数字序列沿定子圆周又是呈周期性的，每过d(q的分母)个数字就会重复一次。我们把这种沿定子圆周一个循环周期内各相依次分得的槽数组成的数字序列，称为分数槽绕组的循环数序。这么说可能太抽象，不好理解，接下来我们仍用上篇讲的Z1=30槽，2p=8极的分数槽绕组作为示例，具体来讲一讲分数槽绕组的循环数序以及如何利用循环数序对分数槽绕组进行分相。

首先把上一篇讲的Z1=30槽，2p=8极的分数槽绕组的槽电势星型图再次展示如下图1所示。

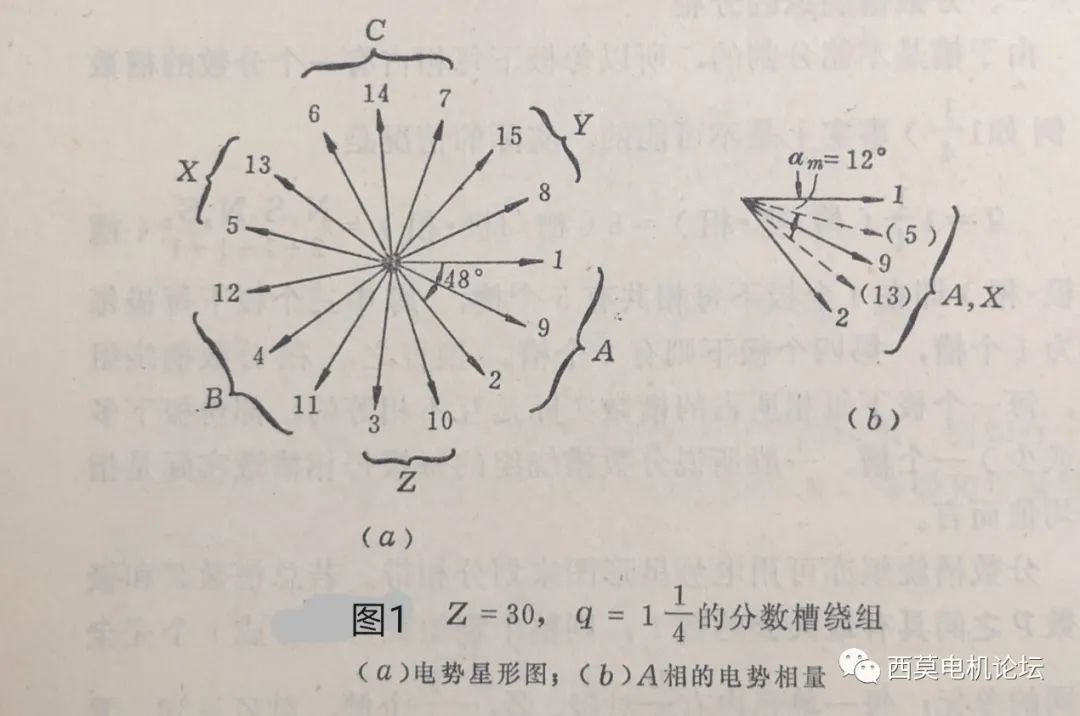
按照图1a的分相结果，把各极下每相分得的槽数列表1如下：

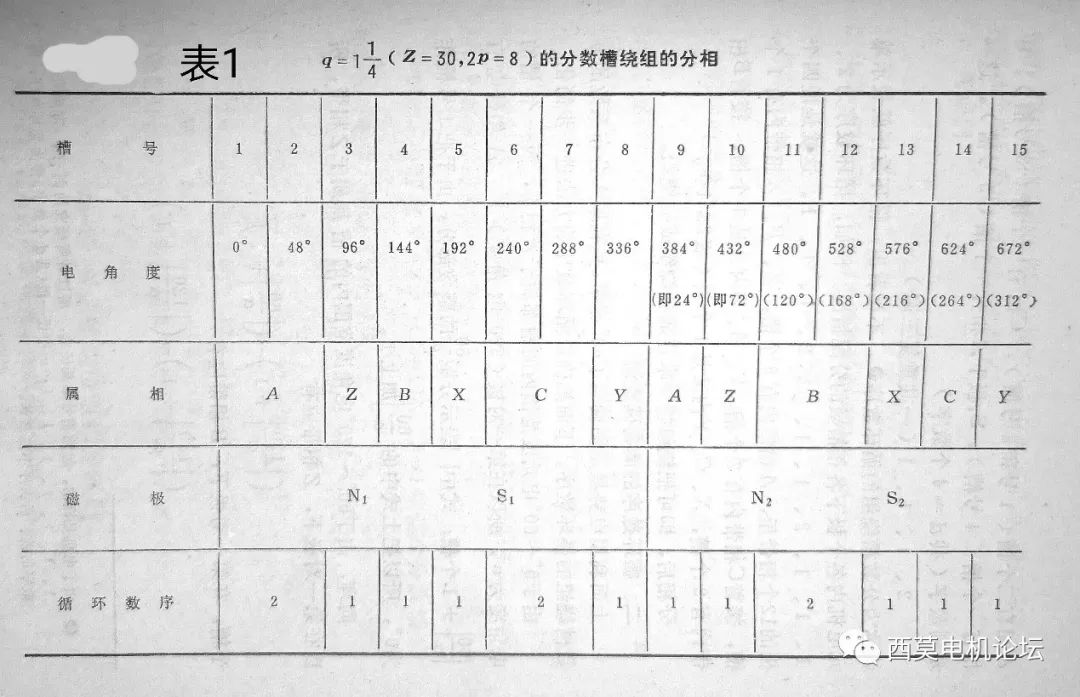
  比较图1a和表1可见，二者是完全对应的。N1极下A相分得二个槽(1#槽和2#槽)，Z(-C)相分得一个槽(3#槽)，B相分得一个槽(4#槽)，S1极下X(-A)相分得一个槽(5#槽)。这一系列数字(共d=4个数字)：2、1、1、1，就称为该分数槽绕组的循环数序，把这四个数字组成的循环数序重复三遍即得到一个单元电机的相带分配结果。也就是说，循环数序就是表示电机内各极下各相槽数的分配规律的一系列数字，就本例而言，循环数序为2、1、1、1，2、1、1、1，2、1、1、1…代表沿定子圆周第一个槽开始，依次给A—Z—B—X—C—Y…各相带分配的槽数。这样只要确定了循环数序，不用画槽电势星型图也能进行相带划分，因此用循环数序进行相带划分是一种简洁的分相方法，特别适用于槽数比较多的分数槽绕组。需要说明的是，由于电机定子是一个闭合的圆周，而第一个起始槽的位置也是可以任意定义的，因此，对本例而言循环数序可以截取2、1、1、1、2、1、1、1…中任一段(共d个数字)作为循环数序，即：1、1、1、2；1、1、2、1；1、2、1、1等都可以作为该分数槽绕组的循环数序。也就是说，同样一个分数槽绕组，其循环数序不是唯一，可以有多种组合，截取循环数序时的起始点可以不同，但数字的前后次序不能互换。

1.2 循环数序与q的关系

知道了什么叫分数槽绕组的循环数序，接下来我们介绍一下循环数序与每极每相槽数q的关系，也就是知道了q之后，如何确定循环数序。由表1不难看出，在利用循环数序沿定子圆周进行相带划分时，各相带分得的槽数是不同的，一部分相带包括的槽数是2，另一部分包括的槽数是1，即存在两种宽度不同的相带，我们把多1槽的相带称为大相带，少1槽的相带称为小相带。不失一般性地说，对于q=b+c/d的分数槽绕组，要实现每个相带包含的平均槽数为q，就必须使一部分相带(大相带)分得b+1个槽，而另一部分相带(小相带)分得b个槽。又因q=b+c/d=(bd+c)/d=N/d，先给每个相带都分b个槽，则d个相带就分去了bd个槽，还剩下c个槽没有被分配下去，要想实现平均每极每相槽数为q，必须要给c个相带中每个相带再加一个槽，即构成c个大相带，d-c个小相带。由此得出结论，当已知每极每相槽数q后，则循环数序数字个数即为d(q的分母)，包括的总槽数为N(q的分子)，也就是把N个槽分成d份，由于d和N不可约，且每一份只能是整数个槽，所以不能均分，只能某些份比另一些份多一个槽。这样形成的一些分配组合就可以作为该分数槽绕组的循环数序。

打个比方，这就相当于把N元钱分成d个红包，每个红包里必须是整数元钱，而且大红包只能比小红包多一块钱，这样每个红包里的钱数组成的数字序列即为循环数序。

仍以上例8极、30槽，q=1+1/4=5/4分数槽绕组为例，把5个槽分成4份的分法可以是q=(2+1+1+1)/4，这样循环数序就是2、1、1、1，当然也可以按1、2、1、1；1、1、2、1；1、1、1、2等组合来分配，这些组合都可以作为该分数槽的循环数序。需要特别说明的是，并不是所有分数槽绕组都可以按上述把N槽分成d份，所有分配组合都可以作为其循环数序，只有当c=1或c=d-1时才能把所有的分配组合都可以作为循环数序。当c≠1或c≠d-1时，按上述方法，只有一部分分配组合可以作为循环数序，因此这种确定循环数序的方法还是有局限性的，需要另外寻求其它确定循环数序的方法。

1.3 循环数序的确定方法

如前所述，同一个分数槽绕组的循环数序有很多种，实践中确定循环数序的方法也有很多，这里介绍常用的几种：

①对于q=b+c/d，其中c=1或c=d-1的分数槽绕组

循环数序由d个数字组成，共bd+c=N个槽，其中c个大相带，每个大相带有(b+1)个槽；d-c个小相带，每个小相带有b个槽。

当c=1时，循环数序中数字的排列顺序一般是(d-c)个小相带的槽数在前面，c=1个大相带的槽数在后面，例如：

q=2+1/4时，循环数序为(2、2、2、3)…

q=1+1/5时，循环数序为(1、1、1、1、2)…

q=2+1/5时，循环数序为(2、2、2、2、3)…

当c=d-1时，一般是c个大相带的槽数排在前面，d-c=1个小相带的槽数排在后面，例如：

q=1+3/4时，循环数序为(2、2、2、1)…

q=2+3/4时，循环数序为(3、3、3、2)…

q=2+16/17时，循环数序为(3、3、3、3、3、3、3、3、3、3、3、3、3、3、3、3、2)…

当然上面所讲的循环数序也可以从任意一个数字开始依次截取d个数字作为循环数序。

②对于q=b+c/d，其中c≠1且c≠d-1的分数槽绕组

这种分数槽绕组的循环数序可用列表方法获得。有两种列表法：

列表法Ⅰ：首先列一个c行d列的表格，从左边第一列开始，从上到下填写等于(b+1)的数字c个，在第二列填写等于b的数字(d-c)个，然后接着又填写等于(b+1)的数字c个及等于b的数字(d-c)个，…余类推，直到c行d列完全填满为止。这时取表中任意一行的数字，都可以作为循环数序。举例说明：

例如：q=1+4/7时，b=1，b+1=2，d=7，c=4，d-c=3，可作出4行7列的表格如下：

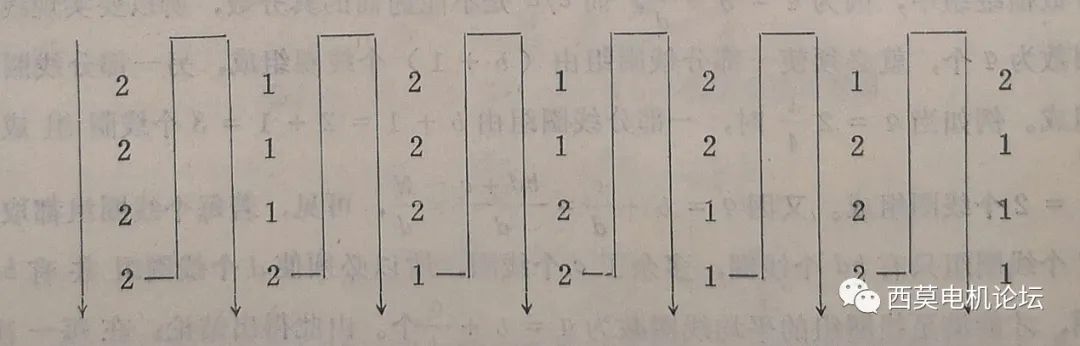
  这时循环数序可取为(2、1，2、1、2、1、2)；(2、1、2、1、2、2、1)；(2、1、2、2、1、2、1)；(2、2、1、2、1、2、1)等等都是可以的。

又如：q=2+2/5时b=2，b+1=3，d=5，c=2，d-c=3，可按上述规则作出2行5列的表格如下：

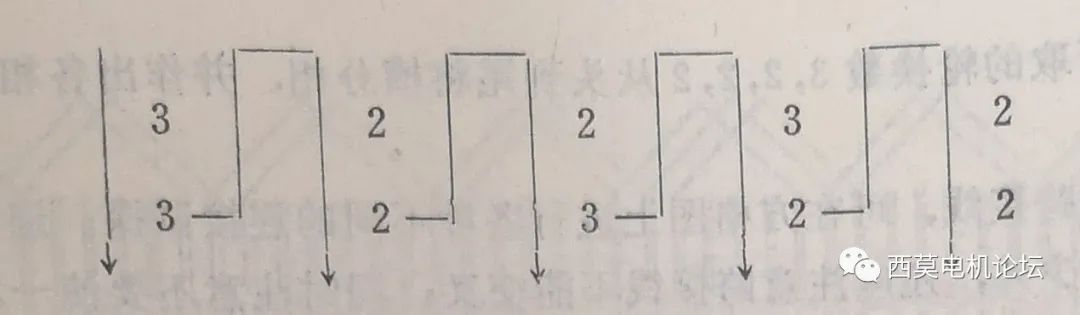
  同理循环数序可取为(3、2、2、3、2)或(3、2、3、2、2)两种都可以。

对于上述类型的分数槽绕组，也可以采用另一种列表的方法：

列表法Ⅱ：列出(d-c)行、d列的表格。从左边开始，自上到下，先填写等于b的数字(d-c)个，接着填写等于(b+1)的数字c个，然后又填写等于b的数字(d-c)个及等于(b+1)的数字c个，直到填满(d-c)行和d列的表格为止。同样，表中任意一行的数字均可作为循环数序。

例如：q=1+4/7，这时，d=7，c=4，d-c=3，列出3行7列的表格如下：

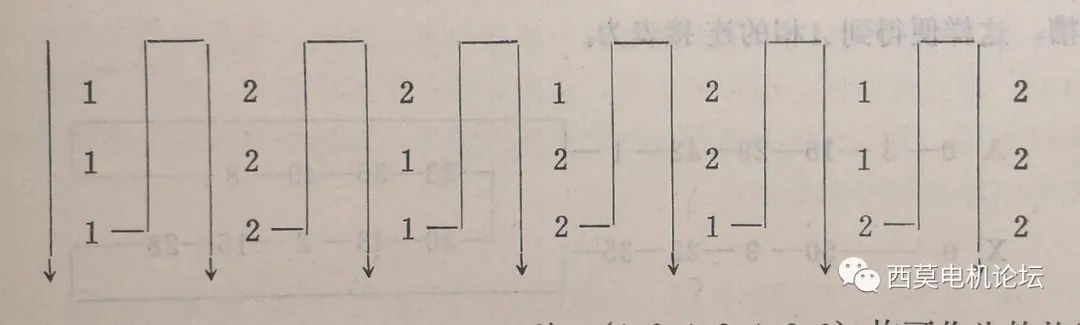
  同理，(1、2、2、1、2、1、2)；(1、2、1、2、2、1、2)；(1、2、1、2、1、2、2)均可作为循环数序。

2 分数槽绕组的构成

与整数槽绕组一样，分数槽绕组按槽内导体层数分也可以分为单层绕组和双层绕组；按线圈组的连接规律分也可以分为叠绕组和波绕组。这里我们重点介绍双层叠绕组和双层波绕组的构成。

2.1 叠绕组的构成

分数槽叠绕组的构成比较简单，基本与整数槽绕组的连接规律一样。仍以Z1=30，2p=8，q=1+1/4的分数槽绕组为例，连接成叠绕组时A相绕组的展开图如图2所示。

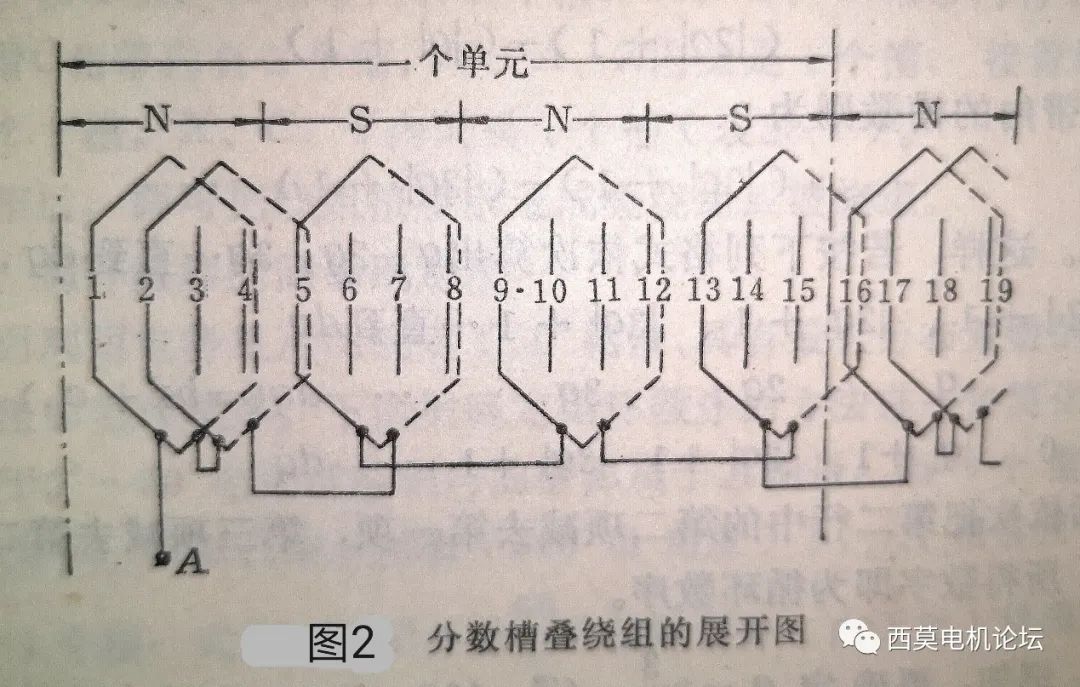
  由表1和图2可见，单元电机内属于A相的共有4个线圈组，其中一个是大线圈组，由两个线圈串联组成；三个是小线圈组，每组内只有一个线圈。不同磁极下的线圈组串联时应该反串，即尾一尾相连或首一首相连，这和整数槽绕组相同。

图1(b)表示A相绕组内各线圈的电势相量，图中5#和13#线圈属于X相带，由于接线时已反串，所以在相量图上其位置翻转了180°，在图1b中用虚线表出。由图1b可见，对所研究的例子，计算A相绕组的合成电势和主波的分布系数时，应该用1、(5)、9、(13)、2等五个互相间隔12º电角度的电势相量来考虑。这是分数槽绕组的一个普遍规律，即普遍来讲，单元电机内A相共有N个(N=bd+c)互相间隔αm电角度的电势相量，αm=60º/N，故计算一相绕组的合成电势时，应该用这N个间隔αm电角度的电势相量叠加来考虑分数槽绕组的分布系数。以上分析可见，分数槽绕组虽然有时槽数较少，特别是微特电机中广泛采用多极少槽设计，通常是q＜1的所谓“分数槽集中绕组”，槽数基本与极数相当，槽数虽少，但可以得到和q比较大的整数槽绕组同样的分布系数和分布效果，这也是分数槽绕组的一大优势和特征。关于分数槽绕组的电势、磁势以及绕组系数的计算分析，后续文章还会详细讲解。

2.2 波绕组的构成

与整数槽波绕组相比，由于分数槽绕组的实际每极每相槽数不相等，因此分数槽波绕组的连接就复杂多了，尤其在槽数较多的情况下，有多种波绕组的连接方式，为了得到最佳的连接方案，往往需要在多种连接方案中进行对比优选。如果把每种连接方式都绘出整个接线图非常费时费力，实践中通常采用一种叫做方格图的办法来确定和显示波绕组的连接规律。

接下来我们以Z1=54，2p=8，的三相分数槽绕组为例，介绍一下方格图的作法以及用方格图进行波绕组连接的原理。

①计算每极每相槽数

q=2+1/4。

②确定循环数序

按前述方法得到该分数槽绕组的循环数序为3、2、2、2。

③确定合成节距Y

Y=Y1+Y2=13≈2τ

④画方格图

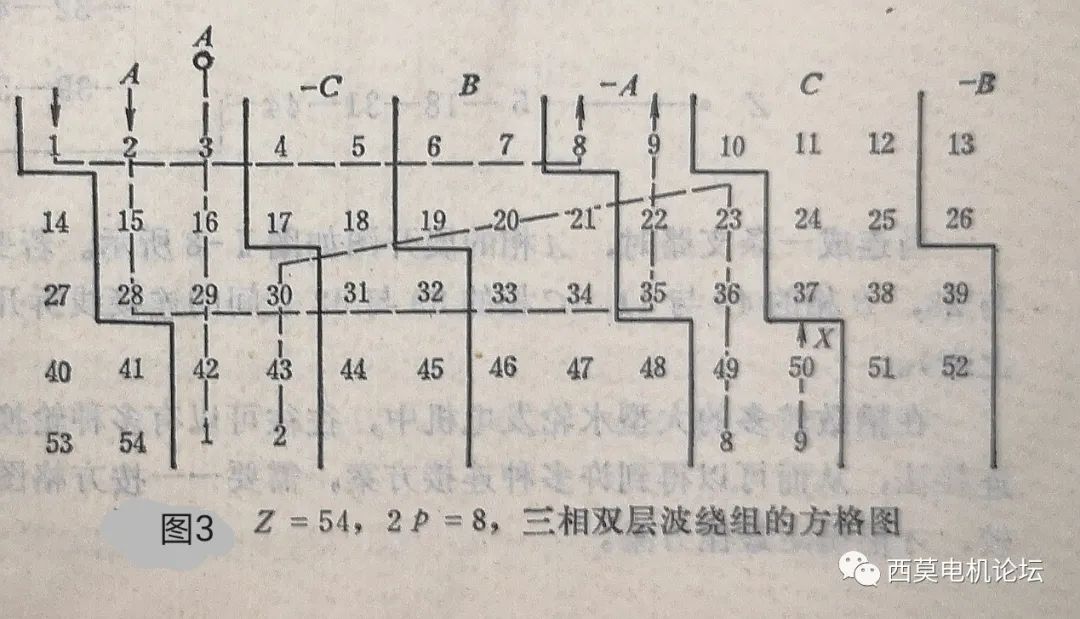
先按1、2、3、4…顺序写出线圈编号，也就是线圈上层边所在的槽号，取每行的槽号数等于合成节距Y(对于本例Y=13)，然后继续依次往下写槽号，直到写完Z1个槽号(对于本例Z1=54)，为了更直观地看清连接规律，通常在写完所有(54个)槽号后，继续往下多写一行或多写几个槽号，如图3所示。

  ⑤相带划分

在方格图上按循环数序3、2、2、2从头到尾将各槽号划分相带，由于各相带的大小不同，因此六个相带的分割线是阶梯型的折线。

⑥线圈连接

为了得到最佳的连接方案，可在方格图上进行各种不同连接方式的试探。线圈连接的原则：一是跨接线尽量短；二是跨接线数目尽量少；三是跨接线尽量不交叉或少交叉；四是一相的所有跨接线要避免在端部形成完整的一圈，以免引起轴向磁场。

根据以上原则，以A相为例，首先从3#槽开始作为A相首端出线头，纵向的各槽，例如3—16—29—42—1，它们之间都相差一个合成节距(13槽)，所以这些线圈都是很自然地按照波绕组的连接规律连接起来，类似这种自然连接的线圈还有30—43—2—15—28；50—9—22—35；23—36—49—8等等。这四段线圈组都是按照波绕组的连接规律自然连接起来的。接下来就是用跨接线把这四段线圈组串联起来。显然1#线圈与8#相隔仅7个槽，距离较近，可以用一根跨接线连接起来；同理再分别用两根跨接线将23#线圈与30#线圈、28#线圈与35#线圈连接起来，就构成了并联支路数为1的全串联A相绕组。其线圈连接的次序和连接规律见下表

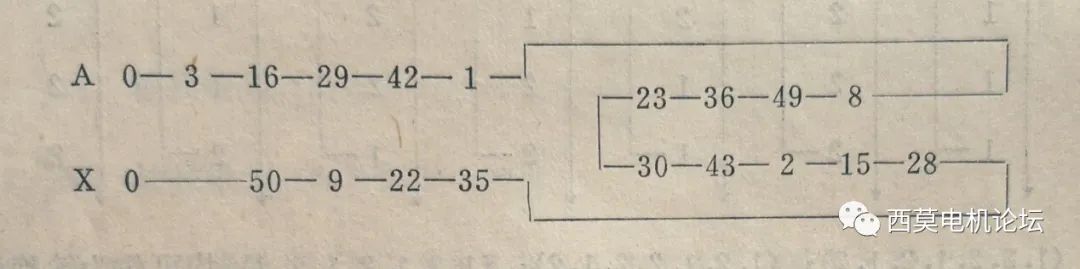
  同理可以进行B相和C相的连接，为了保证三相互差120º，B相可以从21#槽作为出线头开始连接；C相从12#槽起始。因为3#、21#、12#槽电势互差120º电角度。这样就可以得到B相和C相的连接表如下：

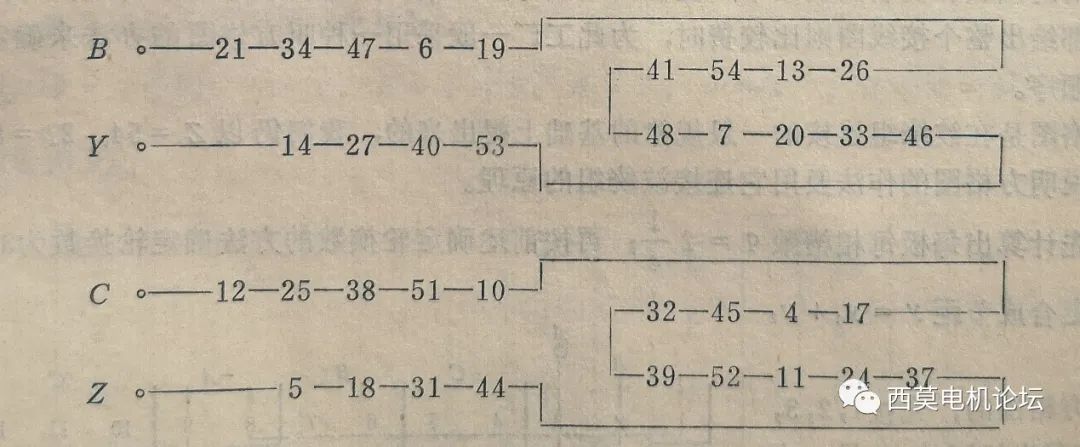
  ⑦画绕组展开图

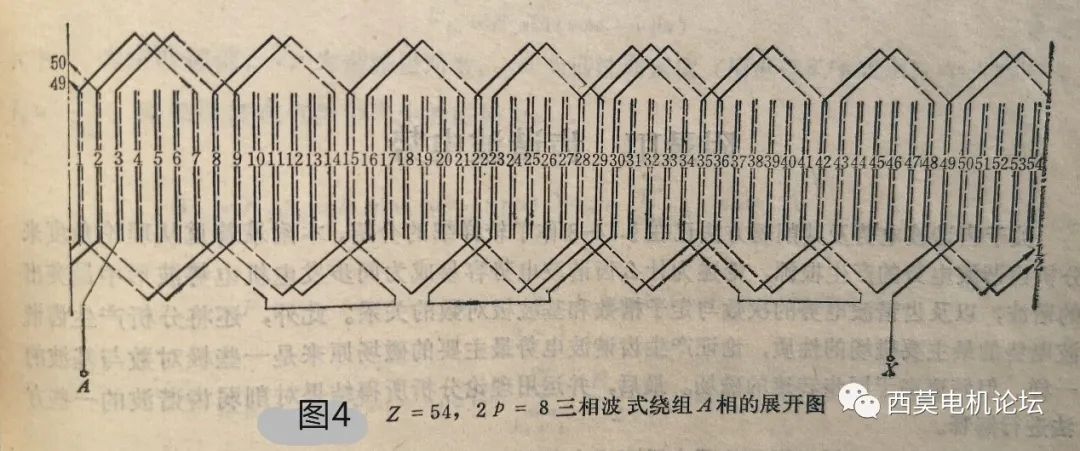
以上三相连接方式是并联支路数为1的连接方式，这种连接的绕组展开图如图4所示。为了清楚起见，图中只画出了A相绕组展开图。

  如果要连接成两路并联的方式，则应将A相的23与30；B相的41与48；C相的32与39之间的三根跨接线断开，这样每相就可以得到两条并联支路。

在槽数较多的大型水轮发电机和低速直驱电机中，往往可以有多种循环数序，每一种循环数序又可能有多种连接方式，从而可以得到许多种连接方案，需要逐一在方格图上进行连接对比，最终确定最佳连接方案。

本期介绍了分数槽绕组的另外一种相带划分和槽分配的方法——循环数序法；还介绍了分数槽叠绕组和波绕组的构成方法。由于叠绕组的构成与整数槽叠绕组构成方法基本相同，相对较为简单；而分数槽波绕组的构成相对要复杂很多，因此重点介绍了分数槽波绕组的构成方法。需要特别说明的是，本期介绍的这些内容和方法，非常适合槽数和极数都比较多，q＞1的分数槽绕组，如大型水轮发电机、低速直驱永磁电机等进行相带划分和绕组连接，并不太适用于微特电机那种槽数较少、多极少槽的分数槽集中绕组，因为这种分数槽绕组往往q＜1，b=0，虽然也可以用循环数序，但由于b=0使得循环数序中出现0数字，非常容易出错。由于这种电机槽数较少，远不如用槽电势星型图进行相带划分和槽分配更加简单直观。由于槽数较少，更不用兴师动众地搞什么方格图做波绕组连接。

编辑：黄飞