计算机基础知识之处理小数1

jf_78858299 2023-03-31 1072

电子说

1.2w人已加入

将0.1累加100次也得不到10

我们来一个计算机运算错误的例子。

function sum(){
    let sum = 0;
    for(let i=1;i<=100;i++){
        sum +=0.1;
    }
    console.log(sum)
}

我们在浏览器的控制台中，运行sum(),得到的运行结果为9.99999999999998。这显然和我们的九年义务教育所教导的 「背道而驰」 。

有句话说， 「雪崩的时候，没有一片雪花是无辜的」 。在这段代码中，程序没错，计算机也没有发生故障，当然和所使用的语言也没有关系（选用其他的高级语言可能运算结果不同）。如果硬要找一个背锅的，那就是 「计算机处理小数的机制」 。

在计算机底层知识之二进制中我们讲过，由于计算机内部所有的信息都是以二进制数的形式来处理，因此， 「整数和小数并无差别」 。

在说明计算机如何用二进制数表示小数的具体方法前，我们先尝试将1011.0011这个有小数点的二进制数转换成十进制数。

小数点 「前面」 部分的转换方法在计算机底层知识之二进制中介绍过。只需将各 「数位」 数值和 「位权」 相乘，然后再将相乘的结果相加即可实现。其实，针对小数点后面的部分，也是 「照猫画虎」 ，也是将各 「数位」 数值和 「位权」 相乘的结果相加即可。

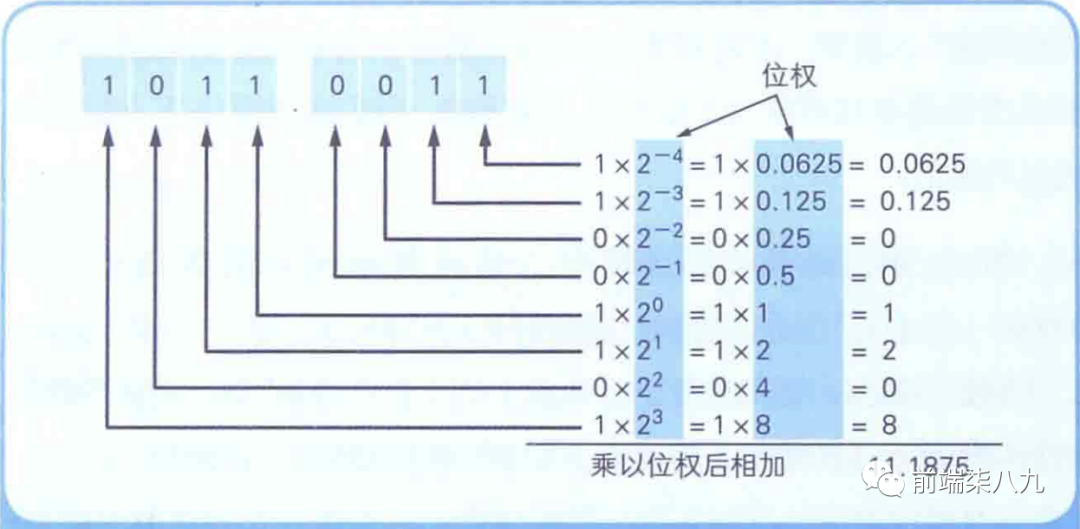
二进制数小数转换成十进制数

二进制数小数点前面部分的**「位权」**

而小数点后面部分的**「位权」**

❝0次幂前面的位的位权按照1次幂、2次幂····的方式**「递增」**

0次幂后面的位的位权按照-1次幂、-2次幂····的方式**「递减」**

❞

❝计算机运算出错的原因：「有一些十进制数的小数无法转换成二进制」

❞

小数点后4位用二进制数表示时的数值范围为0.0000~0.1111。这里只能表示0.5、0.24、0.125、0.0625这四个二进制数小数点后面的位权组合而成（相加总和）的小数。

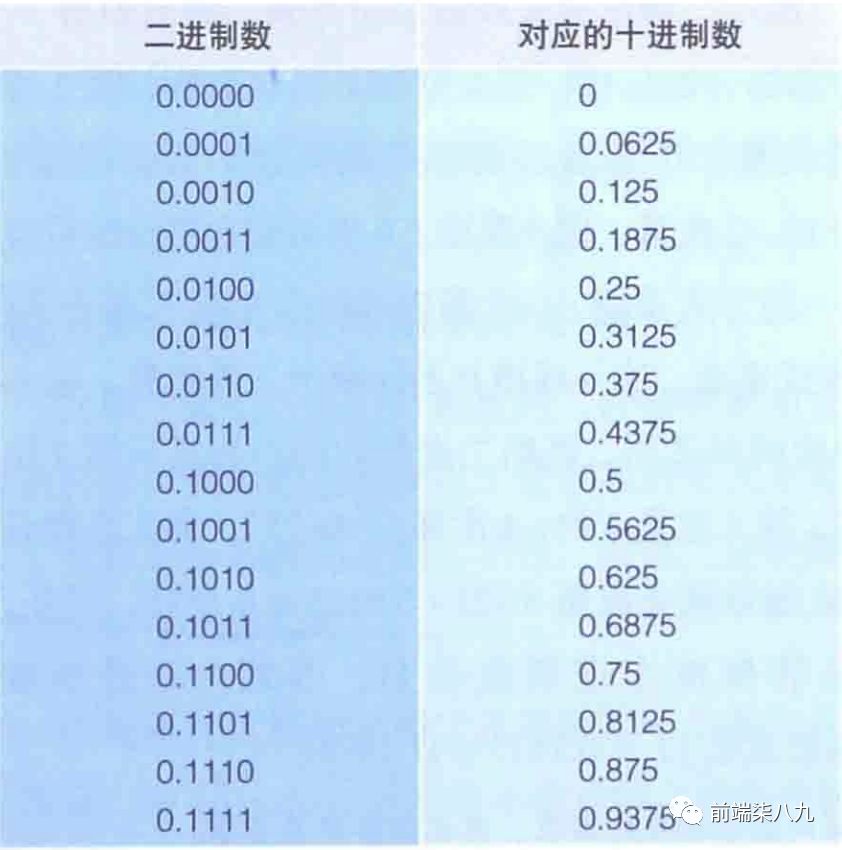
❝可以看出：「二进制数是连续的，十进制数是非连续的」

❞

在前面讲二进制的时候，我们说，根据IC引脚个数不同，我们可以表示位数不同的二进制数。我们可以通过增加引脚数，也就是增加二进制小数点后面的位数，与其相对应的十进制数的个数也会增加， 「但是不管增加多少位，2的-〇〇次幂怎么相加都无法得到0.1这个结果」 。

实际上，十进制数0.1转换成二进制后，会变成0.00011001100···（1100循环）这样的 「循环小数」 。这和用十进制数来表示1/3是一样的道理。

❝计算机这个 「功能有限」 的机器设备，是无法处理 「无限循环」 的小数的

❞

因此，在遇到 「循环小数」 时，计算机就会根据 「变量数据类型」 所对应的长度将数值从 「中间截断」 或者 「四舍五入」 。

然后，我们再结合我们上面的例子，一个 「循环小数」 在进行存储的时候，已经被 「掐头去尾」 ，而偏偏针对这个值，又进行了N多次处理。不怕你不努力，就怕你，持之以恒的向偏离既定轨道的方向上移动，那么结果可想而知，是永远不会达到最终想要的结果。

像1011.0011这样带小数点的表现形式，在计算机内部是无法使用的。

很多编程语言中都提供了两种表示小数的数据类型，分别是 「双精度浮点数」 和 「单精度浮点数」 。

「浮点数」 是指用 「符号」 、 「尾数」 、 「基数」 和 「指数」 这四部分表示的小数。

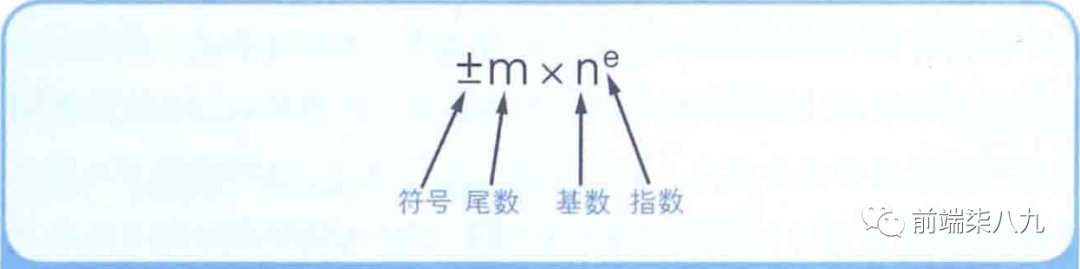
❝计算机内部使用的是二进制数，所以 「基数是2」 ，因此，实际的数据中往往不考虑基数。只用 「符号」 、 「尾数」 、 「指数」 这三部分就可以表示 「浮点数」 。

❞

浮点数的表现方式有很多中，我们采用IEEE标准来解释。

双精度浮点数和单精度浮点数在表示同一个数值时 「使用的位数」 不同。

「符号部分」 是指使用一个 「数据位」 来表示符号。「数据位是1时表示负，为0时表示正或者0」

❝数值的大小用 「尾数部分」 和 「指数部分」 来表示。即用 「尾数部分 × 2的指数部分次幂」 的形式来表示。

❞

打开APP阅读更多精彩内容