内存和磁盘的关系&数据压缩（下）

文件以字节位单位保存

文件是将数据存储在磁盘等存储媒介中的一种形式。程序文件中存储数据的单位是 「字节」 。文件的大小之所以用xxKB、xxMB等来表示，就是因为文件是以字节（B = Byte）为单位来存储的。

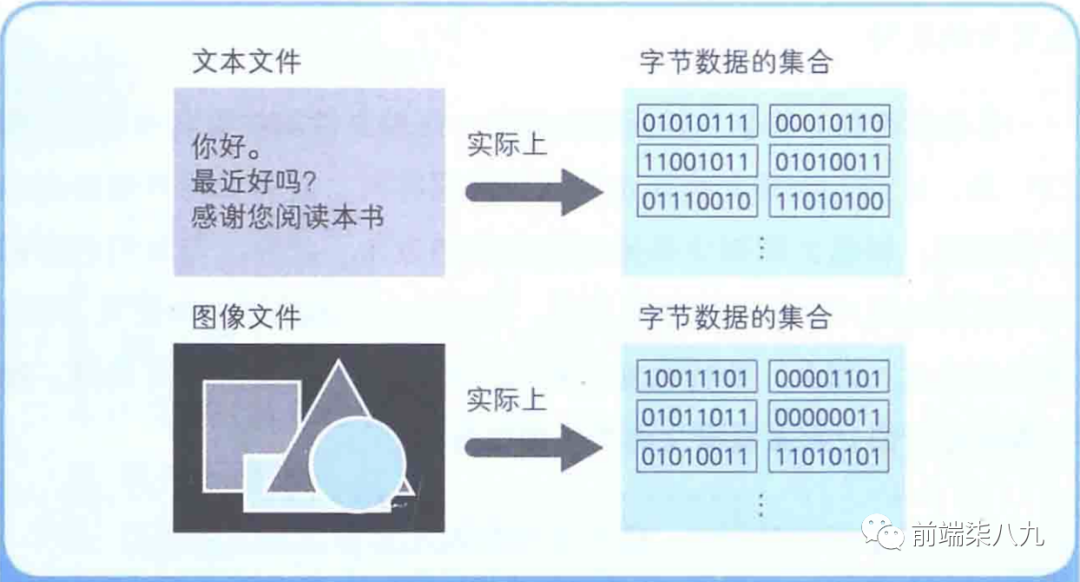
❝文件就是**「字节数据的集合」**

❞

用1字节（=8位）表示的字节数据有256种，用二进制数来表示的话，其范围就是00000000~11111111。

• 如果文件中存储的数据是文字，那么该文件就是**「文本文件」**
• 如果是图形，那么该文件就是 「图像文件」 。

❝在任何情况下，文件中的字节数据都是 「连续存储」 的。

❞

---

RLE算法

我们来尝试对存储着AAAAAABBCDDEEEEEF这17个 「半角字符」 的文本文件进行压缩。

由于半角字母中， 「1个字符是作为1个字节」 的数据被保存在文件中的。因此，上述文件的大小就是17个字节。

我们可以采用将文件的内容用 「字符 × 重复次数」 这样的表现方式来压缩。所以，AAAAAABBCDDEEEEEF就可以用A6B2C1D2E5F1来表示。而A6B2C1D2E5F1是12个字符，那么对应的文本文件就变成了12字节。

12字节÷17字节 ≈70%。也就是采用上述的方式，使得文件压缩到原来大小的70%。

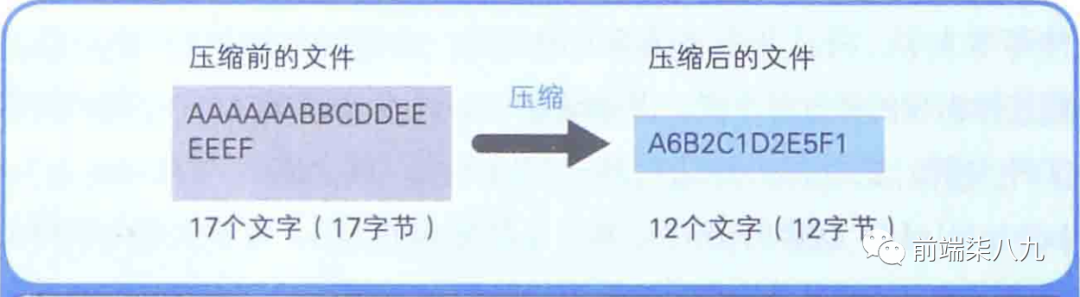
把文件内容用 「数据 × 重复次数」 的形式来表示的压缩方法称为RLE(Run Length Encoding,行程长度编码)算法

RLE算法的缺点

然而在实际的文本文件中，同样字符多次重复出现的情况并不多见。虽然针对 「相同数据经常连续出现」 的图像、文件等，RLE算法可以发挥不错，但是它并不适合文本文件的压缩。

---

哈夫曼算法

「哈夫曼算法」 是哈夫曼与1952年提出来的压缩算法。

针对，哈夫曼算法，首先要抛弃 「半角英文数字的1个字符是1个字节（8位）的数据」 这一概念。

文本文件是由不同类型的字符组合而成的，而且不同的字符出现的次数也是不同的。例如，在某一个文本文件中，A出现了100次，Q出现了3次。

❝ 「哈夫曼算法」 的关键就在于 「多次出现的数据用小于8位的字节数来表示，不常用的数据则用超过8位的字节数来表示」 。

❞

当A和Q都用8位来表示时，原文件的大小就是100次 × 8位 + 3次 × 8位 = 824位，而假设A用2位，Q用10位表示，压缩后的大小就是100次 × 2位 + 3次 × 10位 = 230位。

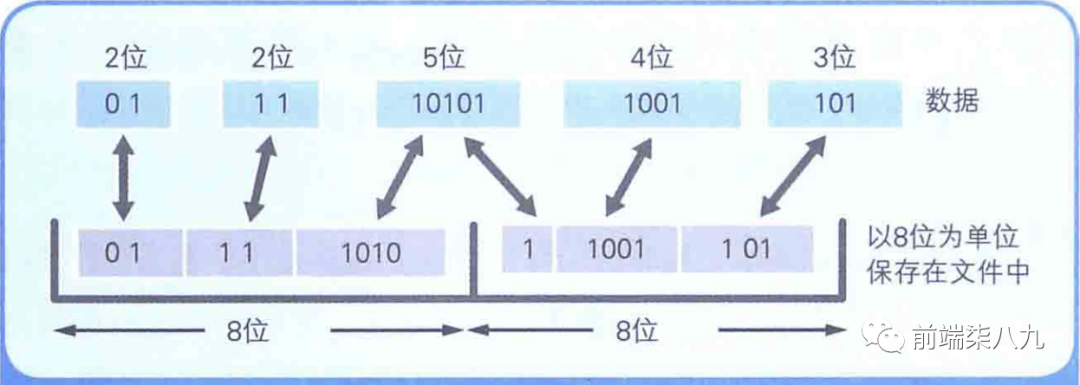
不过，有一点需要注意，

❝不管是不满8位的数据，还是超过8位的数据，最终都要 「以8位为单位保存到文件中」 。

❞

这是因为磁盘是以字节（8位）为单位来保存数据的。

用二叉树实现哈夫曼编码

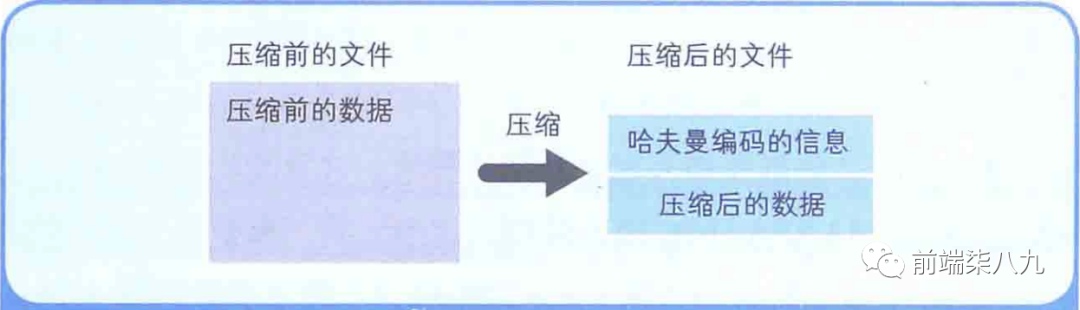
哈夫曼算法是指，为 「各压缩对象文件」 分别构造最佳的编码体系，并以该编码体系为基础来进行压缩。因此，用什么样的编码(哈夫曼编码)对数据进行分割，就要由各个文件而定。

用哈夫曼算法压缩过的文件中，存储着哈夫曼编码信息和压缩过的数据。

在哈夫曼算法中，通过借助 「哈夫曼树」 构造编码体系，即使在不使用字符区分符号的情况下，也可以构建能够明确进行区分的编码体系。也就是说，利用哈夫曼树后，就算表示各字符的数据 「位数」 不同，也能够做成明确区分的编码。

制作哈夫曼树

自然界的树是从根开始生枝长叶，而哈夫曼树是 「从叶生枝，然后再生根」 。

哈夫曼算法能够大幅度提升压缩比率

使用哈夫曼树后，出现 「频率越高的数据所占用的数据位数就越少」 ，而且数据的区分也可以很清晰的实现。

---

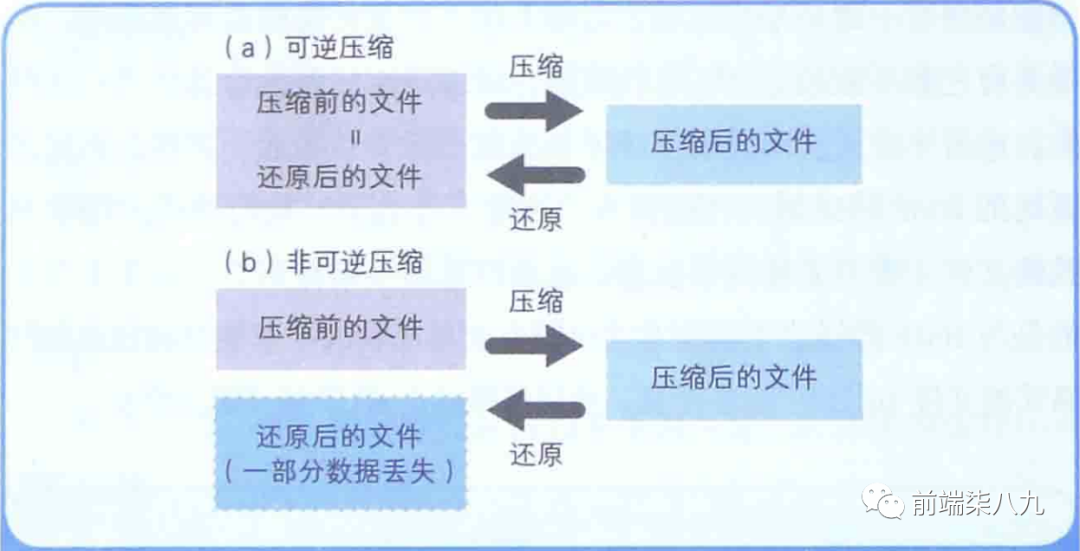
可逆压缩和非可逆压缩

• 「可逆压缩」 ：能还原到压缩前状态的压缩
• 「非可逆压缩」 ：无法还原到压缩前状态的压缩