

使用TDM加快电机仿真分析速度的流程简析
工业控制
描述
1 背景描述
Ansys Maxwell高性能计算技术可帮助用户提高仿真效率,求解更多设计方案、洞察更多设计空间,同时帮助用户创建更准确的ROM。高性能计算包含DSO/LS-DSO、HPC、TDM、DDM等。
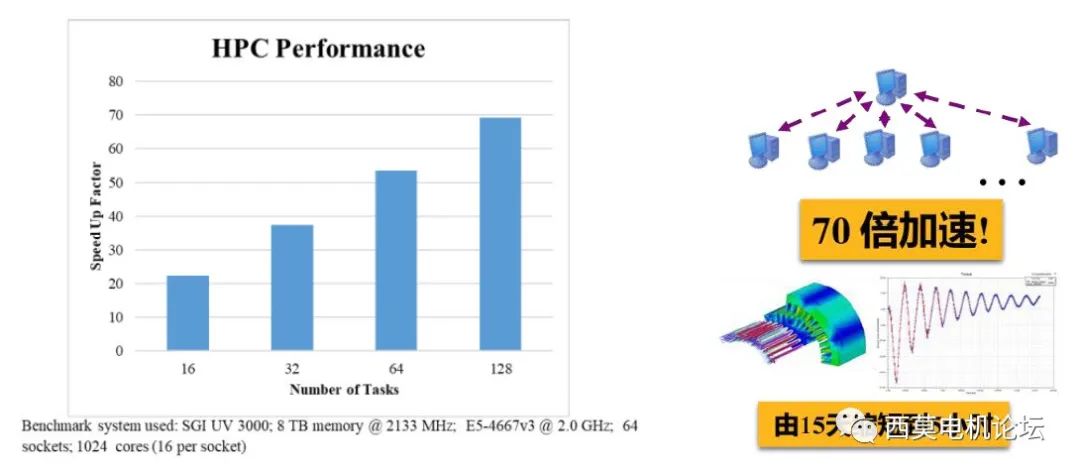
高性能计算
其中DSO/LS-DSO是高效、可扩展、分布式的并行计算解决方案,HPC可以多线程处理大型3D问题,DDM是3D涡流场求解器基于MPI的域分解法,可以对3D涡流场求解器GPU进行加速,而TDM支持如下几种情况:
(1)同时求解多个时间步
(2)普通瞬态
(3)周期性&半周期性
(4)使用TDM求解3D瞬态场源-目标链接。
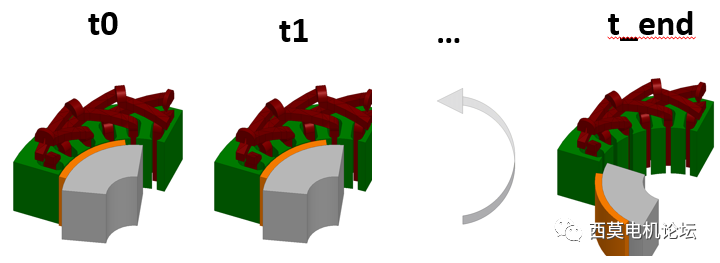
TDM求解
2 TDM功能介绍
TDM(Time Decomposition Method)时间分解法是一种高性能分布式计算的方法,它基于沿时间轴的时域分割来并行计算瞬态场问题,而不是几何分割。
TDM不同于Maxwell常规瞬态算法,它不是顺序求解各个时间步,而是多个时间步同时求解。
TDM可以使用在基于MPI的分布式内存并行平台上。
TDM具有非常好的可扩展性,可以明显加速2D和3D瞬态场问题的求解。
常规瞬态求解算法是按序求解所有的时间步,如下图所示。
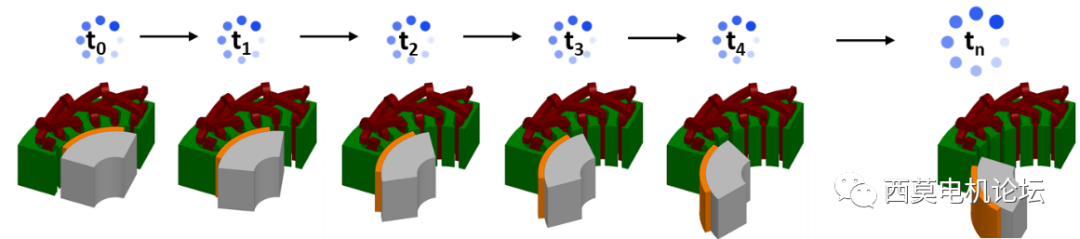
常规瞬态求解算法
而TDM 瞬态求解算法是同时求解所有的时间步,如下图所示。
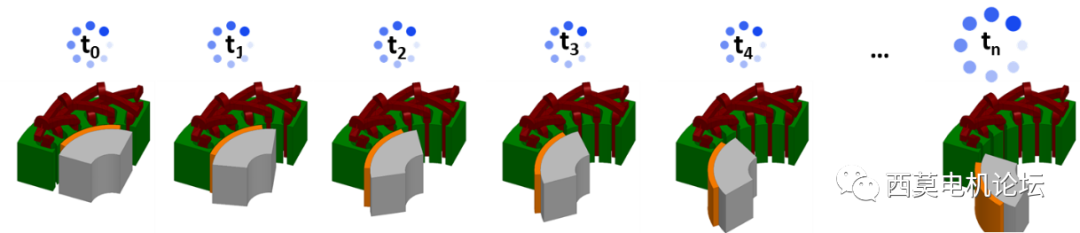
TDM 瞬态求解算法
TDM求解算法中关于Sub-division子时间段的原理图如下图所示。
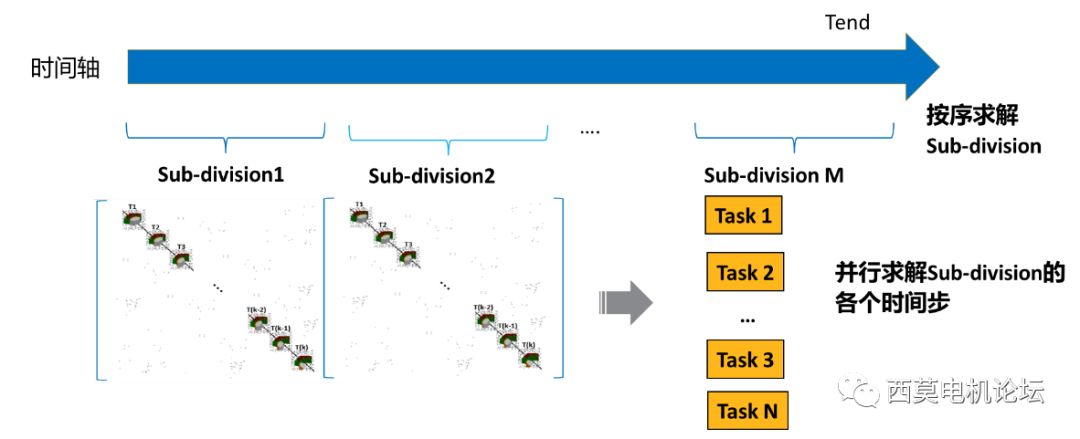
Sub-division子时间段
使用TDM需要进行两处设置,分别是HPC设置及TDM设置。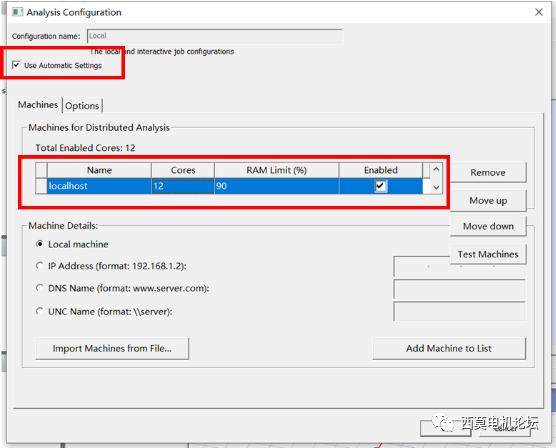
HPC设置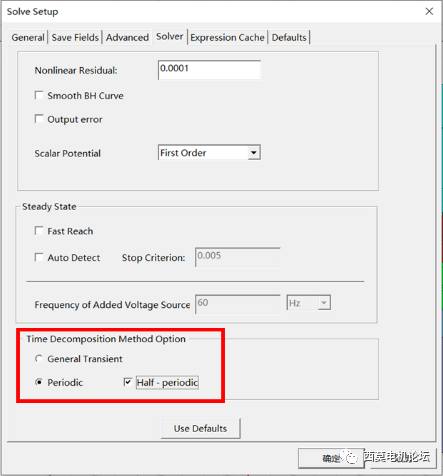
TDM设置
HPC设置方法:首先勾选Use Automatic Settings,通过Num variations distribute设置TDM并行扫参数,Cores用于设置调用的核心数,最大可设置为逻辑处理器核心数。
建议用户按如下推荐进行设置:
协调Timesteps和Cores
使Timesteps/(Cores-1)=整数
由于PeriodicTDM同时对所有时间步进行求解,因此必须确保可用内存大于每个时间步消耗内存*时间步数,并留20%左右余量。

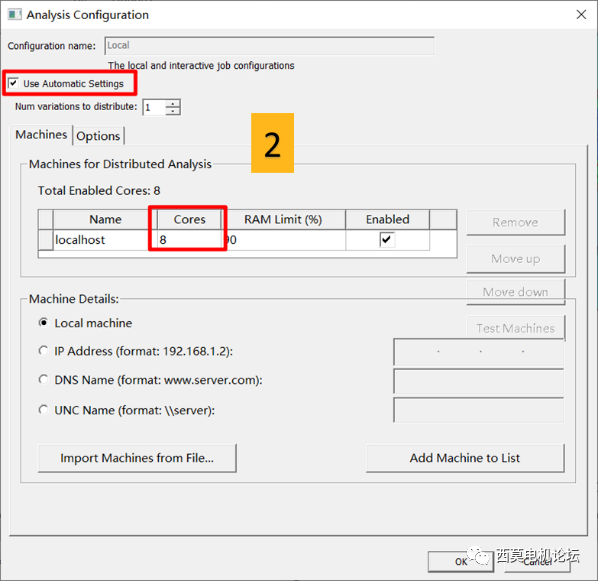
HPC参数设置
TDM有两个选项,包含General Transient常规瞬态求解和Periodic周期性模型。General Transient 常规瞬态求解支持任意的瞬态模型,该方法是最灵活的方法,同时支持涡流效应,可以同时使用快速达到稳定设置“fast reach steady state”。
Periodic周期性模型可以直接达到瞬态稳定状态,如果求解是周期性的,可以使用分布式任务求解一个完整的周期(而且只需要求解一个)。
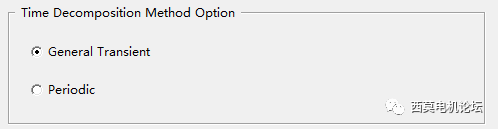
TDM选项
TDM包含周期/半周期TDM。周期TDM设置仿真时间为一个或多个周期,软件只需计算一个周期,直接输出所有周期结果,并直接达到瞬态稳态,典型应用是同步电机的短路分析,感应电机堵转分析。
半周期TDM设置仿真时间为半个周期,软件只需计算半个周期,直接输出一个完整周期结果,典型应用是快速计算同步电机的稳态工况。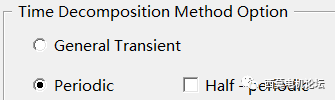
周期TDM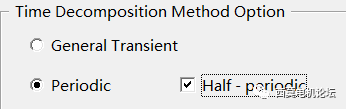
半周期TDM
周期性TDM的限制条件有如下几点。
首先是关于外电路。
由于TDM算法需要同时求解子时间步集合,如果外电路中的PWM波的开关策略要基于历史时间步下的电流结果的话,对于TDM求解器来说,激励源在不同时间步时是未知的,所以这种情况不支持TDM功能,但是如果开关策略是基于时间或位置,则是可以应用TDM功能。
其次是关于机械瞬态。
TDM 不支持机械瞬态,因为TDM必须事先知道每个时间步的移动位置,以便FEA求解器在该预定位置执行计算,机械瞬态显然无法满足这一点。
再次是关于铁损计算。
一个时间步的解不能依赖于几个时间步以前的历史时间步的解(由于时间积分算法自身需要,允许前两个时间步解)。常规的铁损计算是支持的,因为常规的铁损计算是在后处理中完成的。严格来说是不支持磁滞模型,但是对于电机硅钢片这类软磁材料,由于磁滞效应较弱,求解器采用了解耦算法,使TDM支持这种应用,但计算结果与常规算法有一定误差。
最后是关于退磁。
永磁体退磁分析的目的是在瞬态场分析中找到整个瞬态过程中最恶劣的工作点,每当发现新的最恶劣工作点后,软件将使用线性表示的永磁特性来构建新的回复线,该回复线应用于后续时间步的仿真。
因此严格来说,TDM不支持退磁模型,因为TDM必须同时求解某个时间步子集。但是,作为一种合理的近似方案,我们可以基于分布式并行的TDM同时求解某个时间子集,然后在这些已求解的时间步中找到最恶劣的工作点,进一步,最恶劣工作点用于构建一条新的回复线,该回复线用于下一个时间子集的计算。
这意味着找寻最恶劣工作点这项工作是在逐个时间子集中进行的,而不是像在常规计算那样在逐个时间步中进行的。因此通过这种方法找到的最恶劣工作点会与常规计算时有一些不同。但是,从实际应用的角度来看,该解决方案可以被认为是足够准确的。为了尽可能减少误差,可以减少一个时间子集中的时间步数。
3 TDM在永磁电机仿真中的应用
开路和稳态短路分析是永磁同步电机的重点仿真项目,利用Maxwell中的Periodic TDM和Half-Periodic TDM功能,可大幅降低计算量,缩短仿真时间。提高仿真效率。
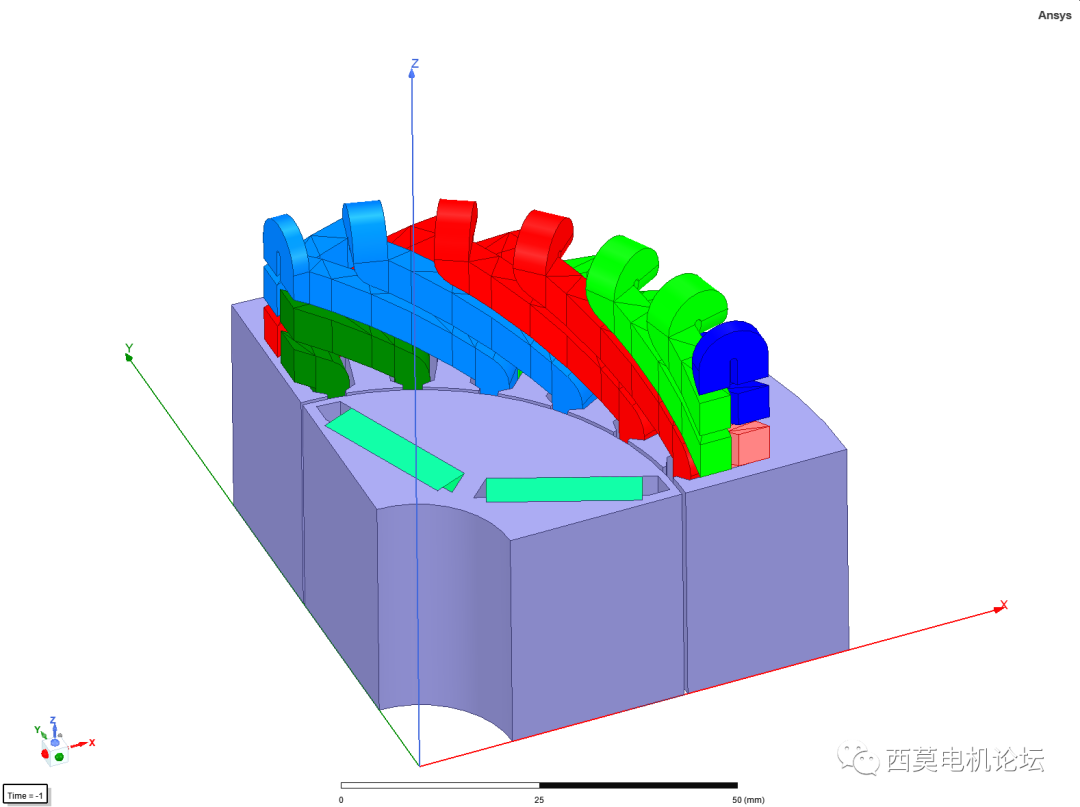
永磁同步电机
首先进行稳态短路分析,采用PeriodicTDM。在Setup>>Sovler处勾选Periodic,本例中电机极数为4极,Stop Time设置为1个电周期,每个电周期30个时间步,实际计算30个时间步。
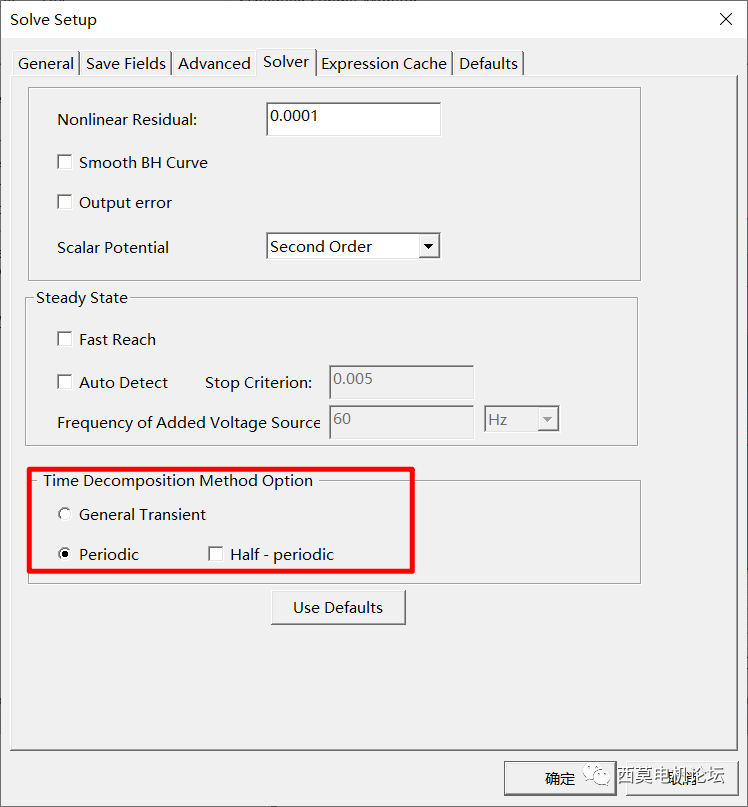
勾选Periodic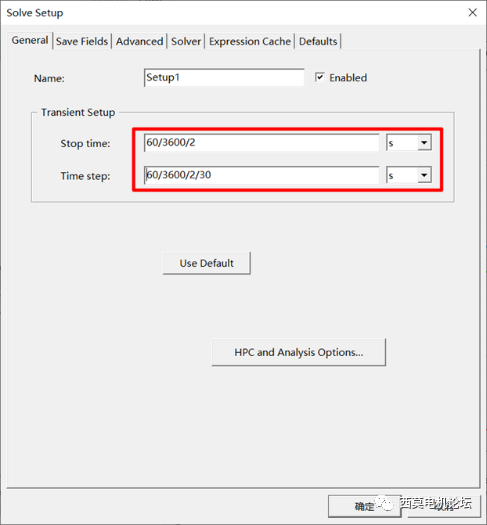
设置计算时间及时间步长
若采用常规方法计算,需要200电周期以上才能稳定,而采用周期TDM,只需1个电周期达到稳定,求解器跳过瞬态迭代过程,直接输出稳态短路电流,求解30个时间步总时间为17分钟。

网格剖分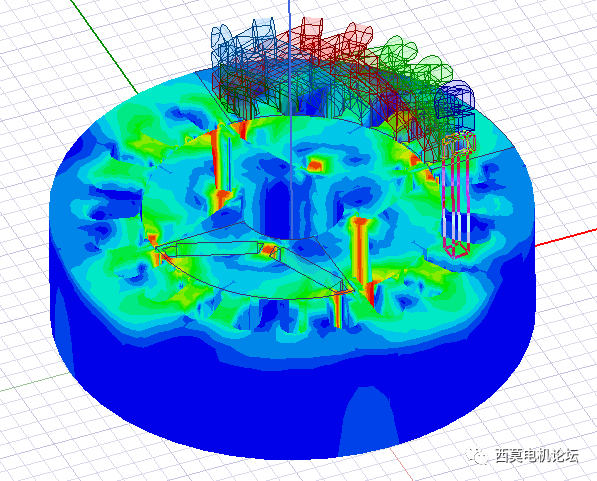
磁密云图
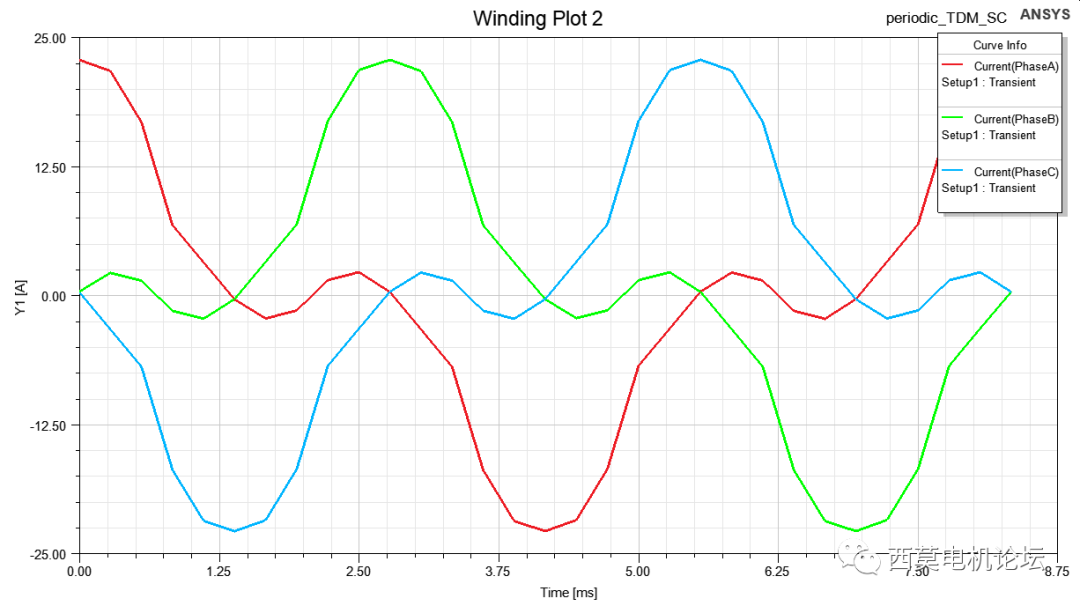
稳态短路电流
用户需要注意的是本例同样适用于Half-Periodic。
接着进行开路分析,采用Half-PeriodicTDM。在Setup>>Sovler处勾选Half-Periodic,采用Half-Periodic求解时,求解模型需符合反对称周期特性,本例中电机极数为4极,Stop Time设置为半个电周期,每个电周期采用60个时间步,实际计算30个时间步。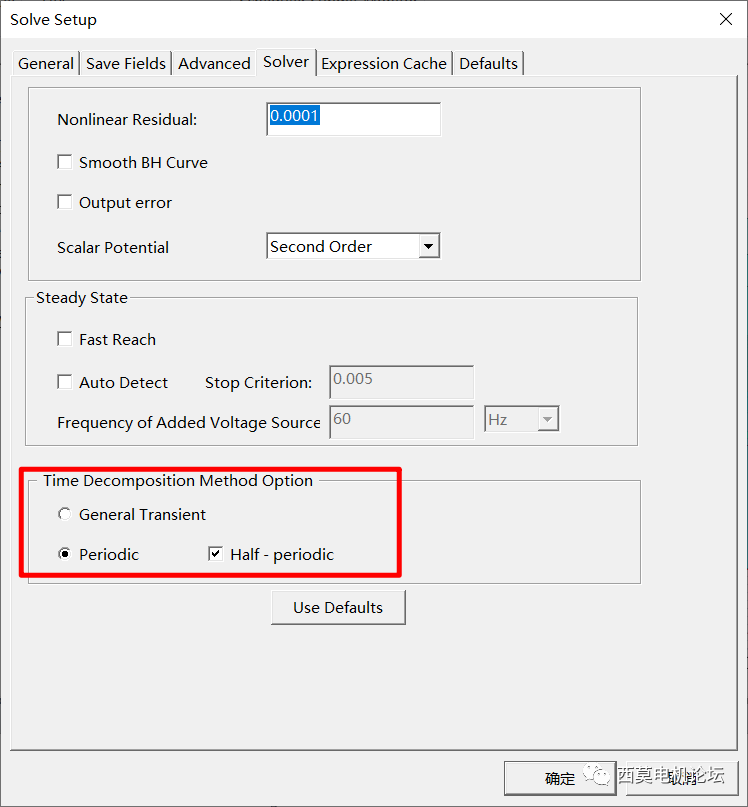
勾选Half-Periodic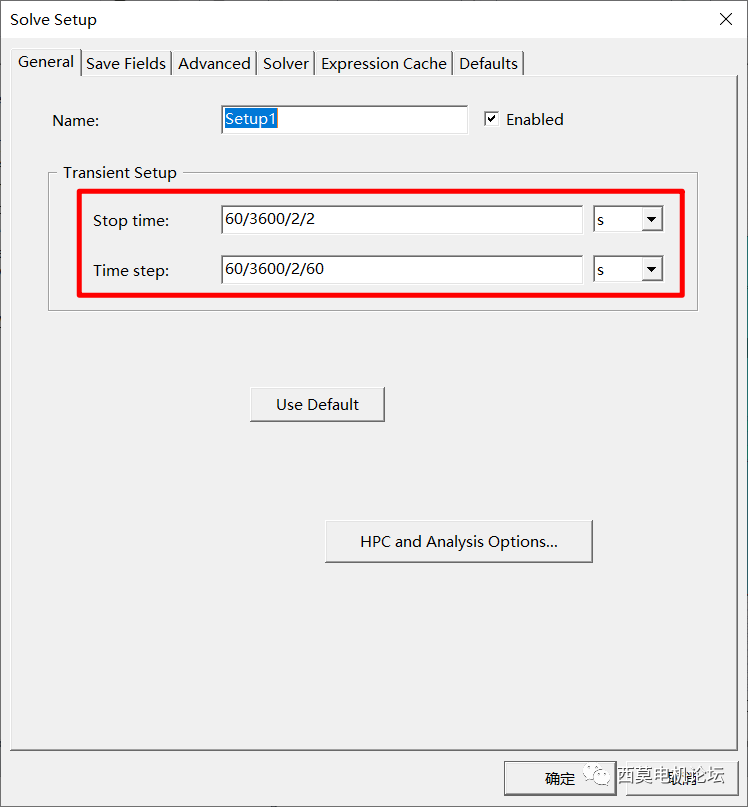
设置计算时间及时间步长
常规计算铁损至少需要一个半周期,采用半周期TDM,仅需计算半个周期,即可输出完整周期铁损、反电势波形,本例求解30个时间步时间为7m30s。
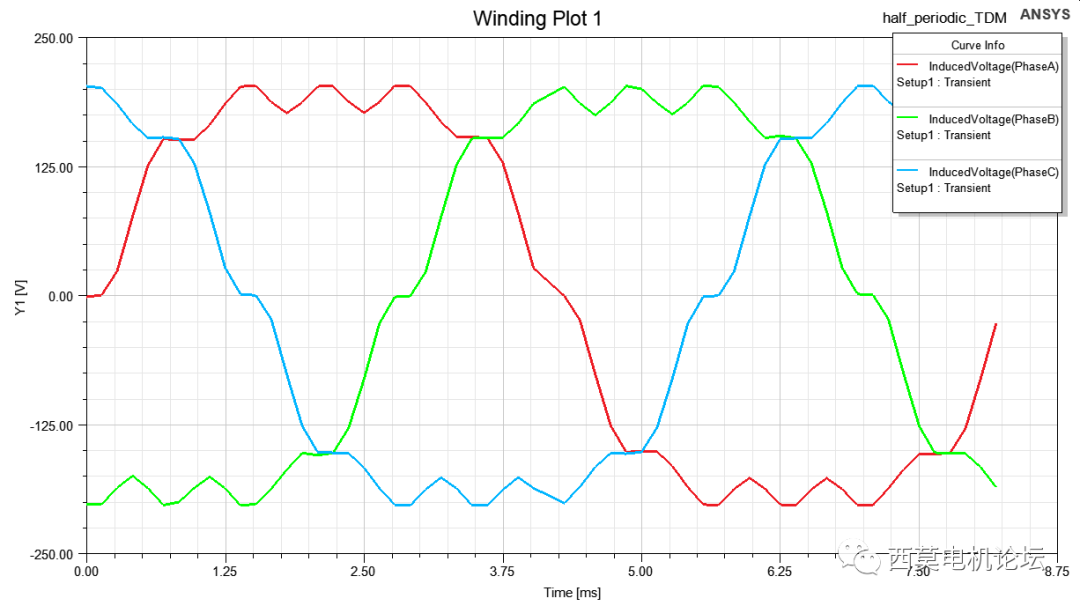
反电势结果
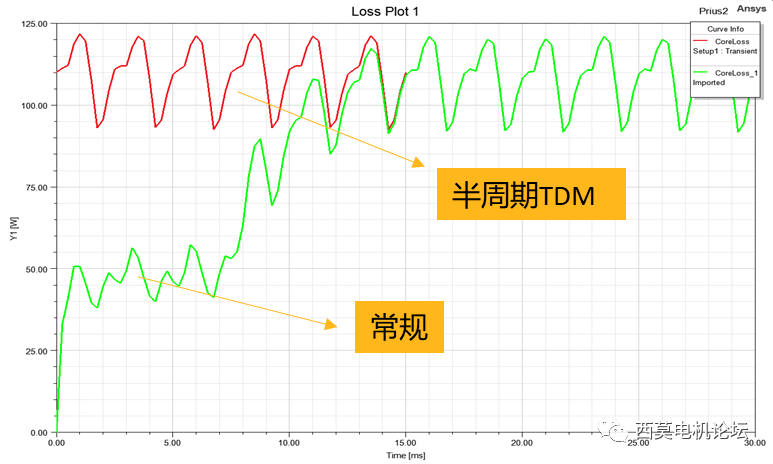
铁损结果
各方案计算的总耗时及反电势结果见下表所示。
| 方案 | 计算时间 | A相反电势rms值/V |
| 无TDM | 36m50s | 159.98 |
| 常规TDM | 17m44s | |
| 周期TDM | 14m52s | 161.08 |
| 半周期TDM | 7m30s |
从上述结果可知,半周期TDM耗时最短,仅为7m30s,计算精度高。
4 TDM在感应电机仿真中的应用
堵转仿真在感应电机分析中比较常见,通常用于计算其堵转转矩和堵转电流,校核电机起动性能。若采用常规分析方法,即使开启Fast Reach和Auto Detect功能,也需要几十个周期才能收敛,这将花费很长的计算时间,若使用周期TDM可以一个周期直达稳态,可以大幅降低求解计算量,提高仿真效率。
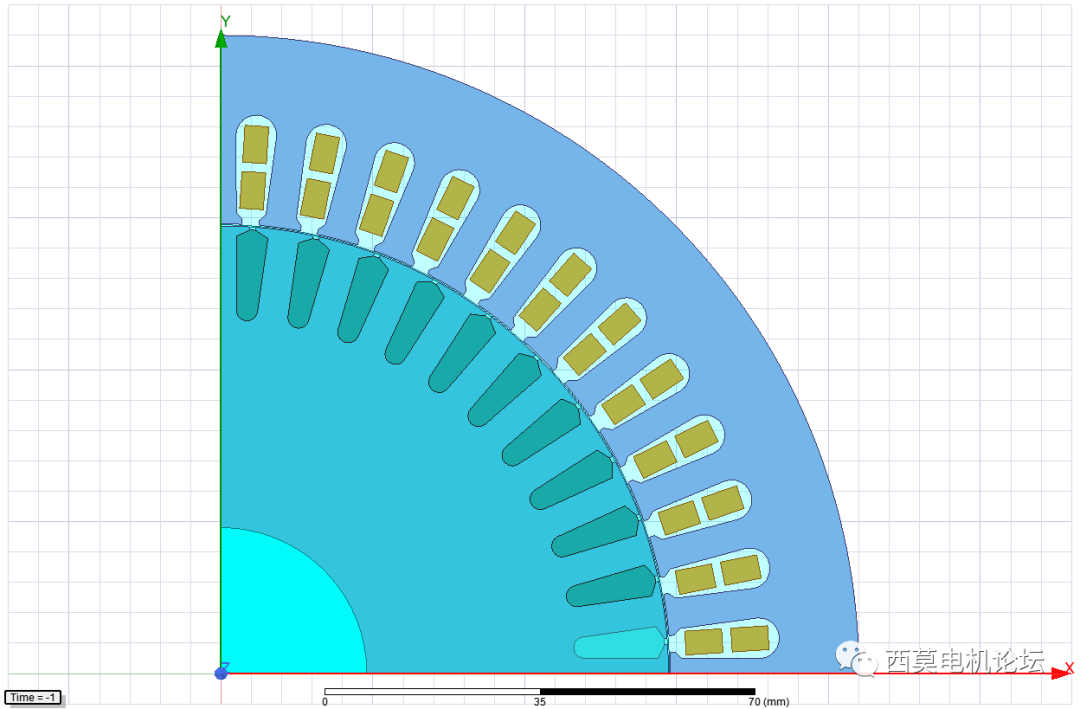
感应电机
堵转仿真
首先测试不使用TDM,单核计算单任务,设置如下。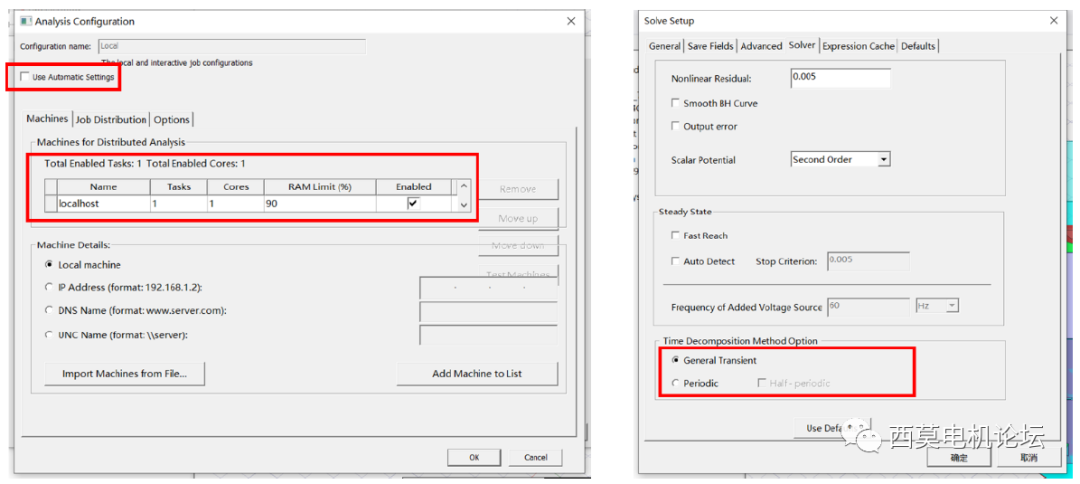
不使用TDM
仿真40个电周期后转矩趋于稳定,计算时间耗时3min48sec。
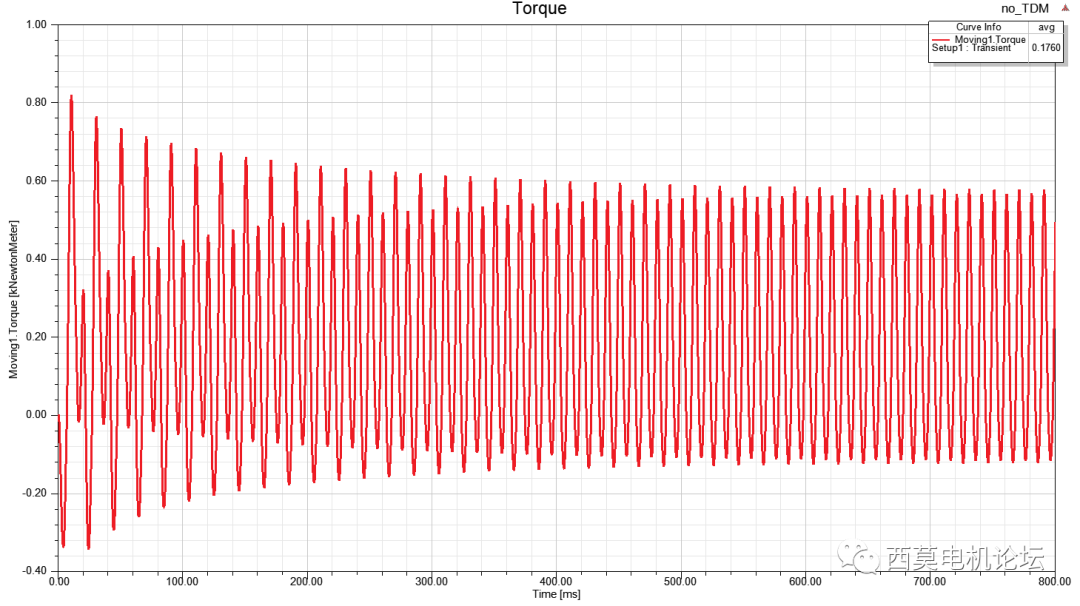
转矩vs时间
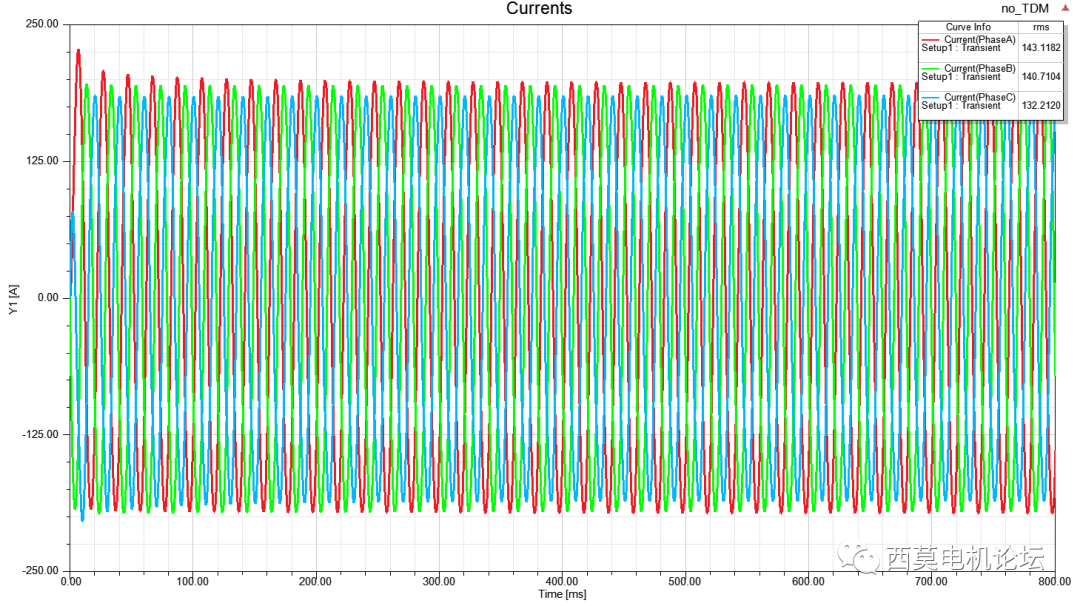
电流vs时间
接着测试使用周期TDM进行计算,设置如下。 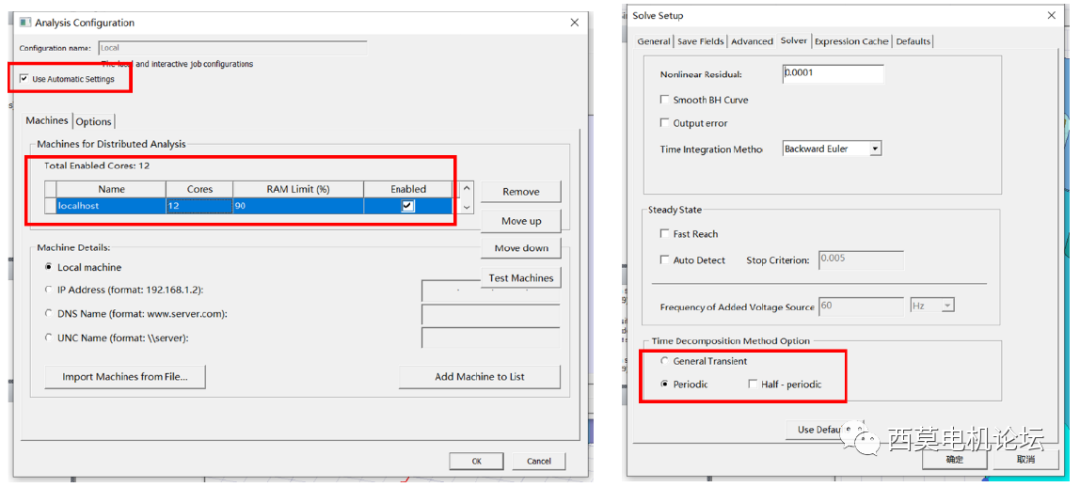
使用周期TDM
只需仿真一个电周期,即可直接达到稳态,计算耗时0min57sec。
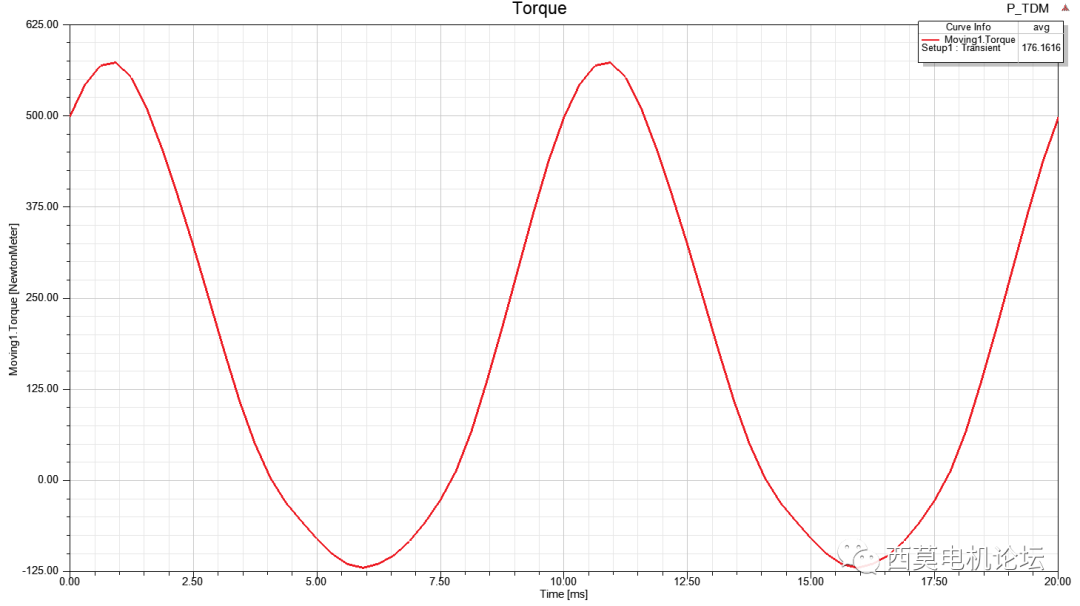
转矩vs时间
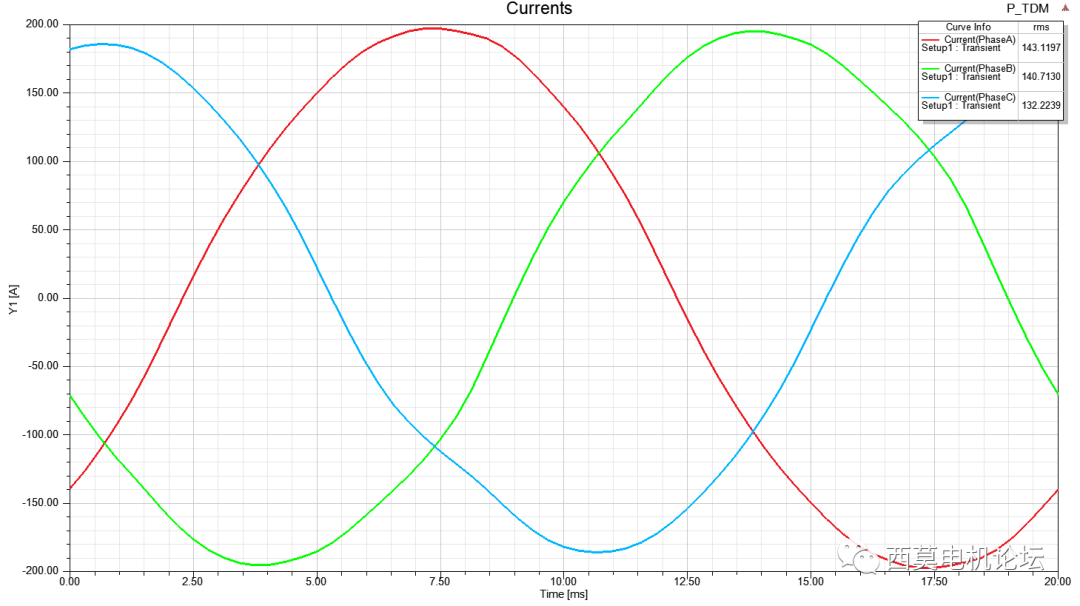
电流vs时间
最后测试使用半周期TDM进行计算,设置如下。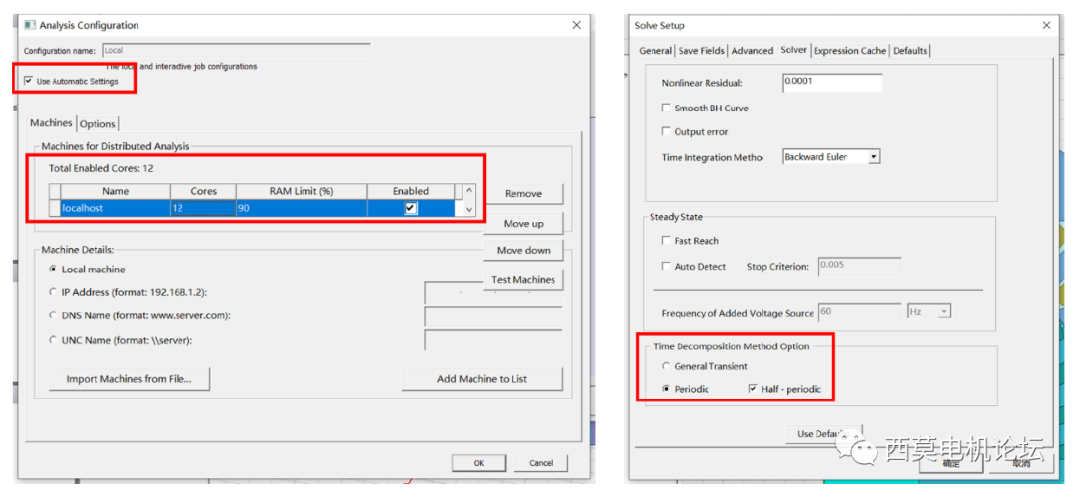
使用半周期TDM
只需仿真半个电周期,软件自动给出稳定后一个完整电周期的结果,计算耗时0min21sec。
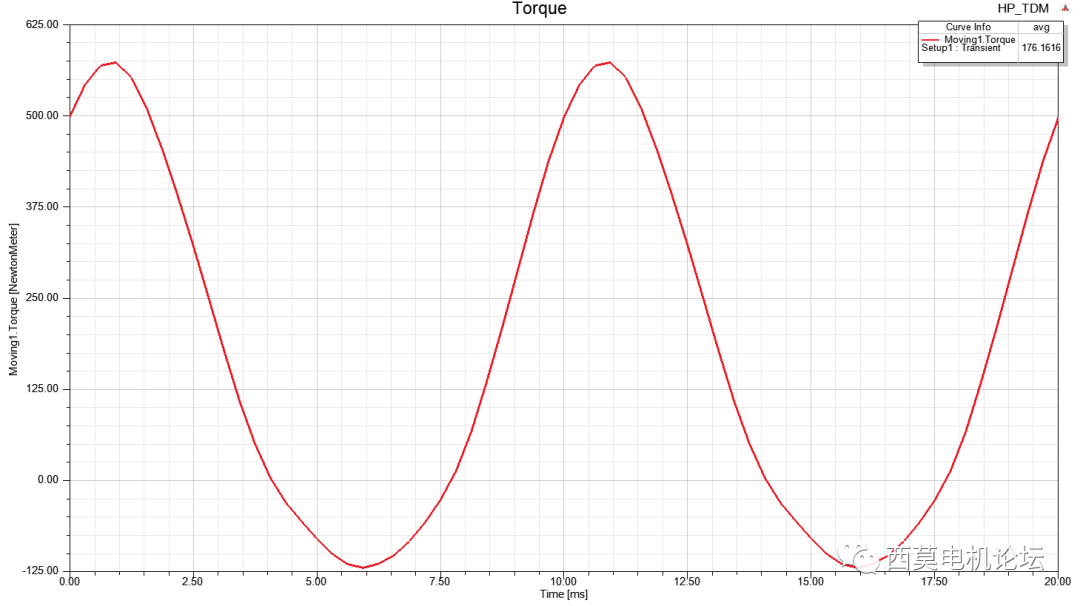
转矩vs时间
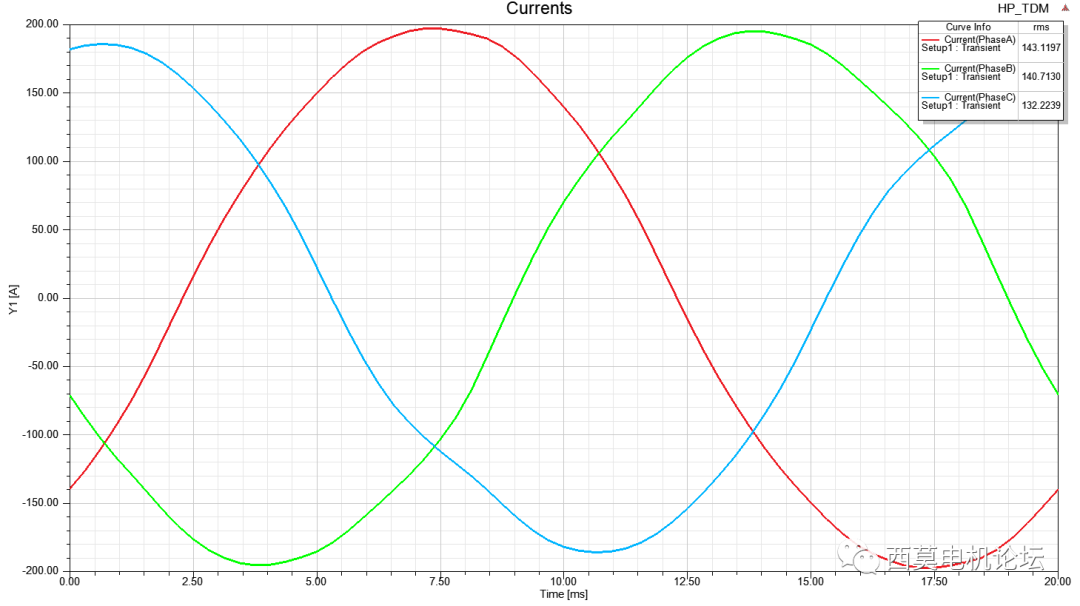
电流vs时间
四种计算方法所用计算时间及转矩与电流值结果如下表所示。
| 计算方法 | 计算时间 | 转矩平均值/Nm | A相电流rms值/A |
| 无TDM | 3m48s | 176.0478 | 143.1182 |
| 常规TDM | 4m36s | ||
| 周期TDM | 0m57s | 176.1616 | 143.1197 |
| 半周期TDM | 0m21s |
从结果可以看出,正常顺序求解和常规TDM计算时间相近,而利用周期性TDM功能可大幅降低感应电机堵转工况仿真时间,且精度可靠。
周期性TDM与无TDM计算的堵转电流与堵转转矩结果对比见下图所示。
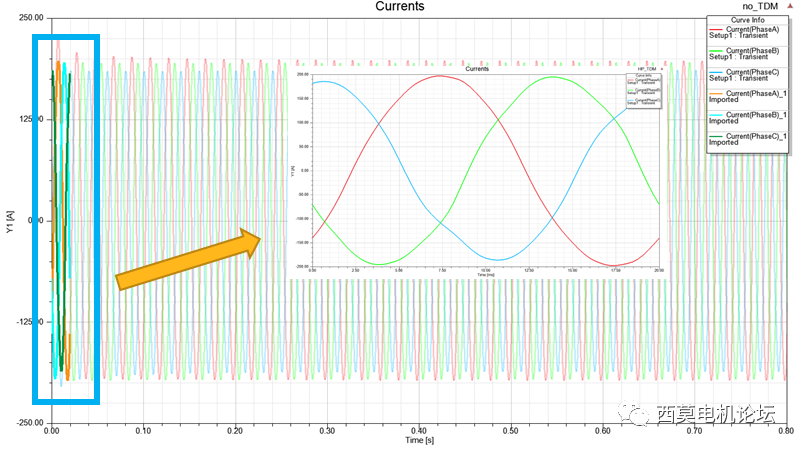
堵转电流
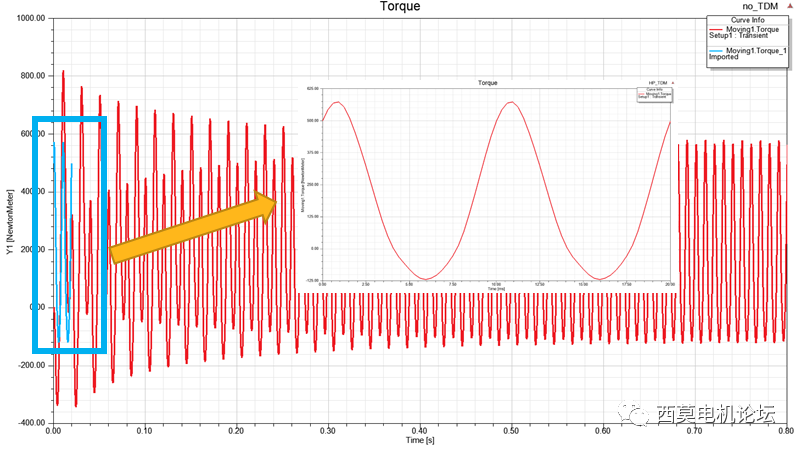
堵转转矩
当案例中有参数化扫描需求时,周期性TDM方式具有非常大的优势。以一转子初始位置角度进行扫描为例,对比不同TDM计算方式总时间。常规TDM与周期TDM计算的转矩结果见下图所示。
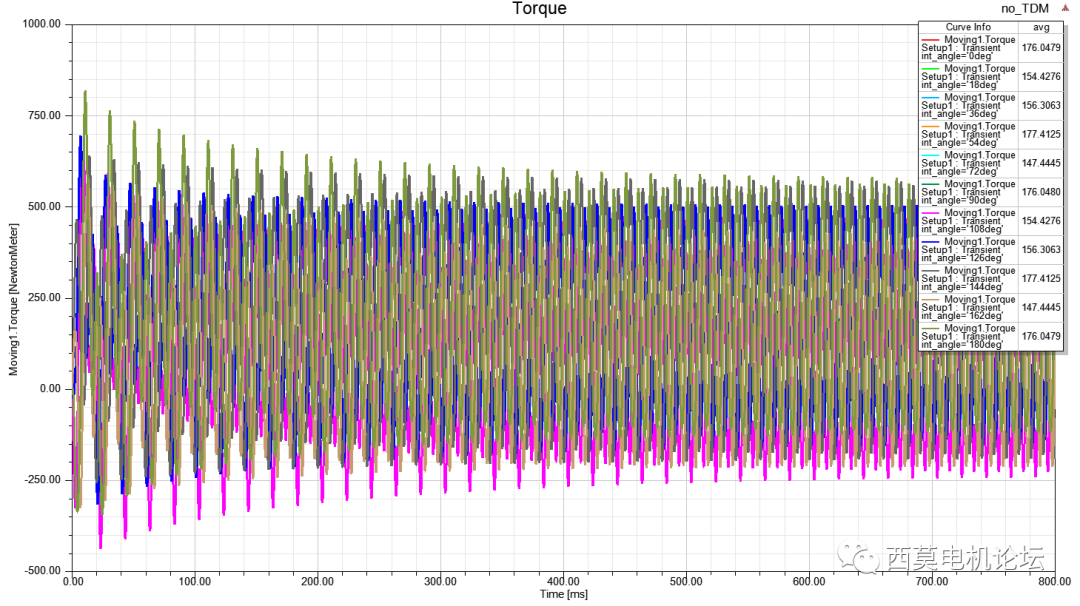
常规TDM
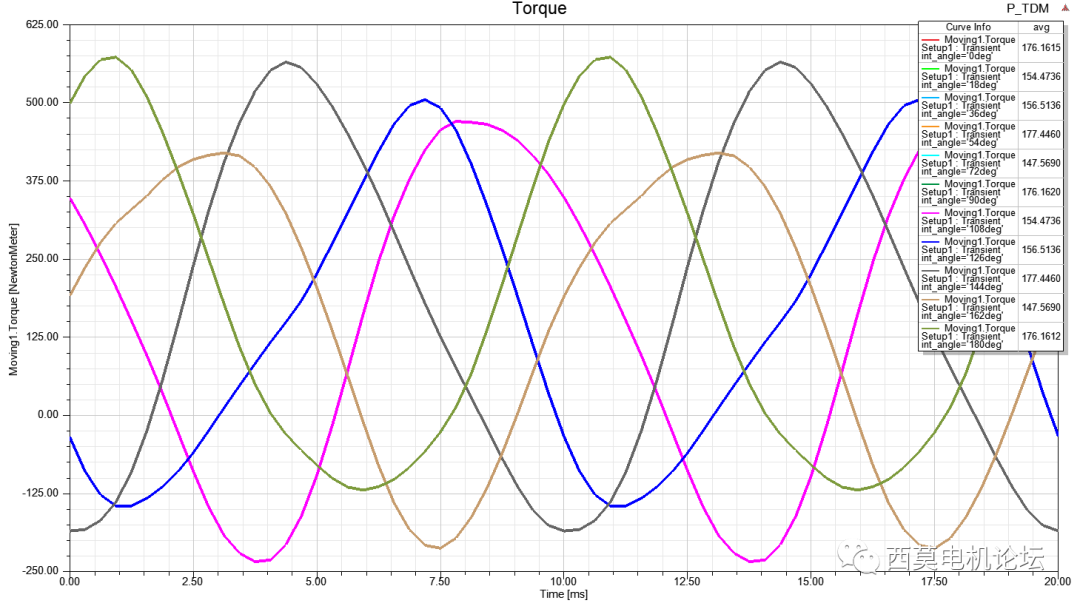
周期TDM
计算时间对比如下表所示。
| 计算方法 | 计算时间 |
| 常规TDM(40个电周期) | 1h16m49s |
| 周期TDM | 13m18s |
| 半周期TDM | 6m40s |
从结果可以看出,当采用常规TDM时,由于无法预测各初始位置角时达到稳态所需时间,本例中统一采用40个电周期进行计算,然而某些初始位置角达到稳态的时间可能小于或者大于40个电周期,在这种情况下,准确评估电机堵转性能有较大困难。当采用周期性TDM时,程序直接给出稳定后的仿真结果,这极大缩短了总体仿真时间
因此,当案例中有参数化扫描需求时,周期性TDM求解方式具有非常大的优势。
5 TDM在ECE提取中的应用
在Maxwell有限元场计算中,有限元模型对电流和转子位置角扫描,扫描后得到的有限元结果通过降阶模型保存在数据表中形成ECE模型,可将ECE模型直接在Simplorer(Twin Builder)进行分析计算,也可以将ECE模型送到控制当中进行高级控制系统仿真。
等效抽取的结果是基于有限元计算得到的数据表,在控制系统联合仿真过程中只需通过查表的方法就能得到电机的性能,因此将抽取后的结果应用到系统仿真中,既保证了精度也提高了速度。
接下来分别测试两个模型,分别是少单元数模型和中等单元数模型。
首先是少单元数模型,系统参数及模型参数信息如下:
操作系统:Windows7
软件版本:MaxwellR19.0
可用核数:10个物理内核(若使用超线程,20个虚拟内核)
测试模型:Prius 2DMotor
单元总数:1634
总数据点数:13671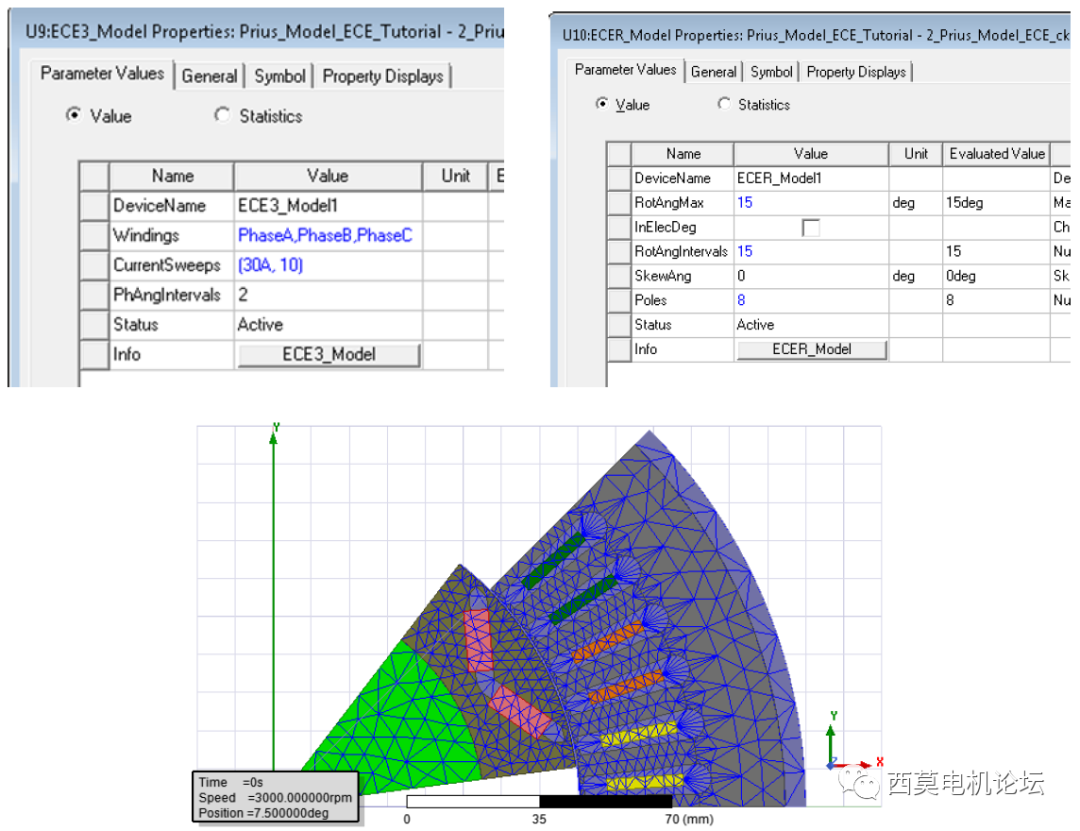
少单元数模型(1634单元数目)
计算耗时结果如下表所示。
| HPC Setting | Cores | Time/min | Time % |
| NON | 1 | 79 | 100 |
| TDM - Auto | 2 | 85 | 108 |
| TDM- Auto | 4 | 39 | 49 |
| TDM- Auto | 8 | 28 | 35 |
| TDM- Auto | 16 (hyperthreading) | 36 | 46 |
| Regular HPC | 16(hyperthreading) | 82 | 104 |
接下来是中等单元数模型,系统参数及模型参数信息如下:
操作系统:Windows7
软件版本:MaxwellR19.0
可用核数:10个物理内核(若使用超线程,20个虚拟内核)
测试模型:Prius 2DMotor
单元总数:16286
总数据点数:13671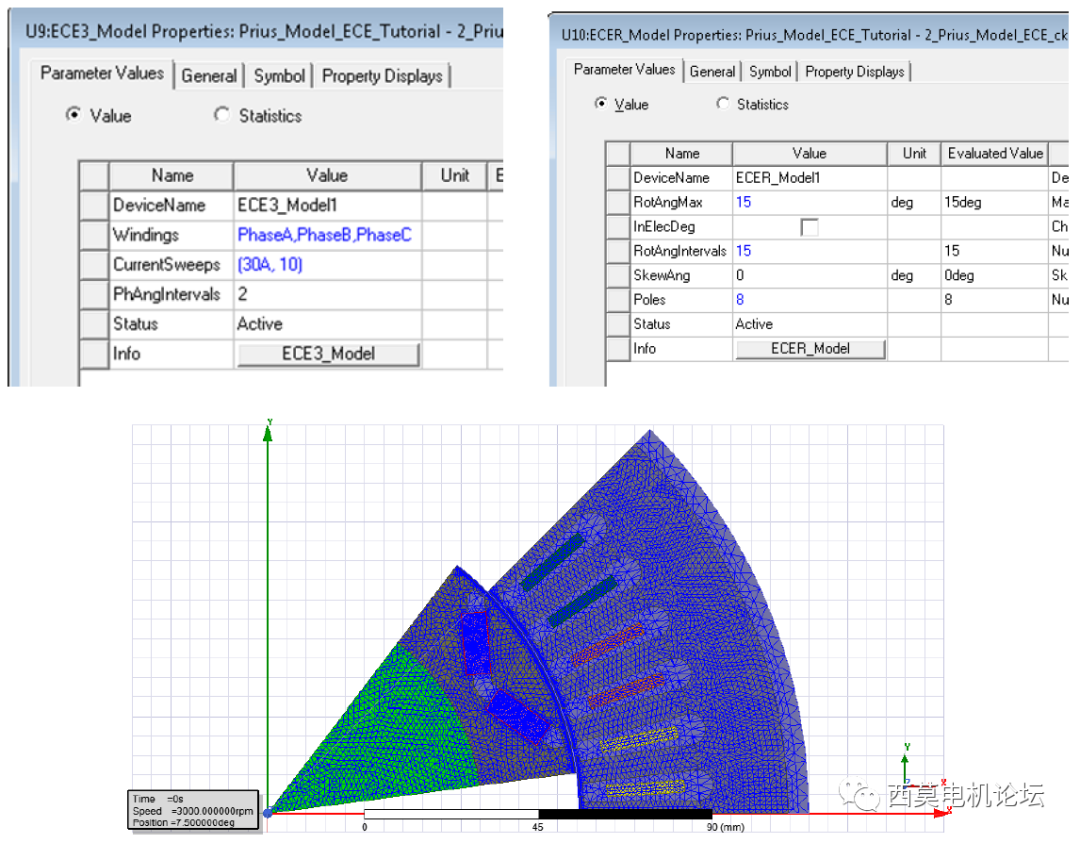
中等单元数模型(16286单元数目)
计算耗时结果如下表所示。
| HPC Setting | Cores | Time/min | Time % |
| NON | 1 | 347 | 100 |
| TDM - Auto | 2 | 361 | 104 |
| TDM- Auto | 4 | 312 | 90 |
| TDM- Auto | 8 | 149 | 43 |
| TDM- Auto | 16 (hyperthreading) | 110 | 32 |
| Regular HPC | 16(hyperthreading) | 360 | 104 |
6 总结
TDM时间分解法是一种高性能分布式计算的方法,它基于沿时间轴的时域分割来并行计算瞬态场问题。TDM主要优点总结如下:
(1) TDM可以实现多时间步的并行求解,充分利用计算机资源;
(2) 周期TDM对于同步电机稳态短路工况仿真只需一个周期即可收敛,大幅降低计算量;
(3) 周期TDM对于同步电机正常稳态工况也有价值,减少铁损计算周期数;
(4) 周期TDM对于感应电机堵转工况的快速收敛有极大的帮助;
(5) TDM可大幅提高电机ECE模型提取速度。
总之,TDM时间分解法可帮助用户提高仿真效率,求解更多设计方案、洞察更多设计空间,同时帮助用户创建更准确的ROM。
审核编辑:刘清
-
Saber软件仿真流程2010-05-17 977
-
笔记本屏幕亮度与反应速度简析2010-01-23 987
-
TDM网络,TDM网络是什么意思2010-04-03 13890
-
电机的数学模型与仿真分析2021-05-19 1017
-
UM3016 如何使用STM32电机控制SDSK v6.0分析器2022-11-22 614
-
简析电动汽车充电桩检测技术应用及分析2024-02-26 2413
全部0条评论

快来发表一下你的评论吧 !

