Frenet坐标系，自动驾驶“混乱”的源头

人类驾驶员在道路上开车的时候，没有人会去基于当前距离出点的横向和纵向距离是多少，而去决定下一步的方向盘转角大小。通常情况，我们只会关注车辆当前距离左右车道线的距离，来判断是否偏离车道，是否需要打方向盘进行方向微调。

自动驾驶运动规划也在效仿这一过程，而为了让这一过程得以实施，2010年，BMW的Moritz Werling在2010年的论文《Optimal Trajectory Generation for Dynamic Street Scenarios in a Frene´t Frame》中提出了Frenet坐标系。

没错，还是国外人发明，我们整天鼓吹自动驾驶第一大国，但看看自动驾驶常用的基础理论、经典架构、基础软件、经典算法……，有多少是我们的发明创造！每个场景都炒一波自动驾驶概念，每个概念都拉一波融资，每一波融资都用来重复造轮子……。大而不强，是自动驾驶继承自汽车产业的顽疾。

Frenet坐标下的出现，让规划、控制有了方向，但也从此开启了自动驾驶万国混战的源头。

01Frenet坐标系的定义

Frenet坐标系的建立基于一个参考线，这个参考线可以是任意曲线，但在自动驾驶运动规划中一般定义为道路的中心线，这条中心线是地图模块输入过来的一系列离散点。同时使用参考线的切线向量和法线向量建立一个直角坐标系，如图1所示，这个坐标系就是Frenet坐标系。

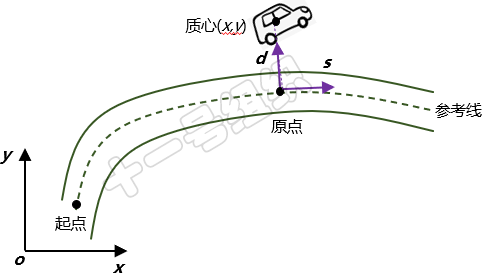
图1 Frenet坐标系示意图

某一时刻，假设车辆质心在全局笛卡尔坐标系下的坐标为（x，y），车辆质心到参考线上的投影点称为原点，原点切线方向称为s轴方向或纵轴方向，原点法线方向称为d轴方向或横轴方向。纵坐标s值指的是参考线上的原点与起点之间曲线的长度，也就是车辆在道路上的纵向行驶距离。横坐标d值指的是原点与车辆质心之间的距离，也就是车辆偏离道路中心线的距离。车辆质心随着时间在不断变化，因此Frenet坐标系的原点也在不断变换，所以Frenet坐标系是一个移动坐标系。

02为什么使用Frenet坐标系

（一）道路表达直观

假设现在我们知道笛卡尔坐标系下车辆的位置为（x，y），在道路通常都有一定曲率的背景下，从这个坐标中我们无法得知道路在哪里，也不知道车辆行驶了多远，更难以确定它是否偏离车道中心。当然我们可以从输入的高精地图数据进行计算获得上述数据，但是计算量太大，因此用笛卡尔坐标系描述道路会非常复杂。

而在Frenet坐标系中，横轴和纵轴相互垂直且原点所在参考线与车道中心线平行，容易确定车辆偏离车道中心线的距离以及车辆沿车道中心线的行驶距离。因此使用Frenet坐标系可以忽略道路曲率的影响，让道路表达更加直观、简洁。

（二）简化路径规划问题

运动规划是为了获得车辆在未来一段时间内具有前瞻性的行驶轨迹，这个轨迹是一种由二维空间和一维时间组成的三维空间中的曲线。

在笛卡尔坐标系下，整车的横向运动、纵向运动耦合在一起，想要计算清楚两者的关系还是需要费一番苦力的。而在Frenet坐标系中，距离参考线的位置可以使用纵向距离s和横向距离d分别表示，而通过对时间分别求导，又可以得到纵向运动速度和横向运动速度。

车辆的二维运动问题在Frenet坐标系下被解耦成两个一维运动问题，而一维优化问题要比二维优化问题更容易容易求解。因此相比于笛卡尔坐标系，Frenet坐标系可以明显地简化运动规划问题，这就是运动规划中笛卡尔坐标系转换为Frenet坐标系的必要性。

下面我们用一个例子来解释Frenet坐标系的这种降维作用。假设行为决策层判断前方有低速行驶的车辆，随后在t0时刻做出了一个在t1时刻完成变道的决策。即车辆需要在Δt=（t1-t0）时间内，横向上需要完成一个Δd以及纵向上完成一个Δs的移动。如图2所示，我们可以将s和d分别表示为关于t的函数：s（t）和d（t），这样二维运动规划问题被分割成了两个独立的一维优化问题。

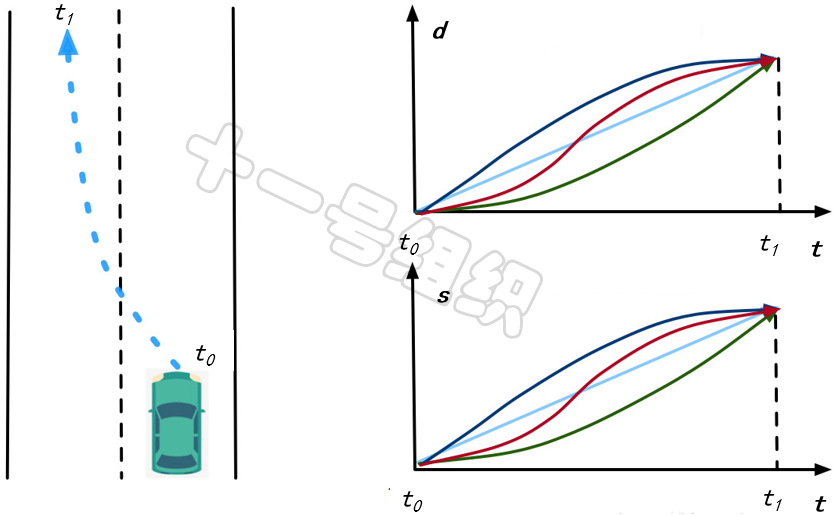
图2 Frenet坐标系下运动规划示例

03Frenet坐标系与笛卡尔坐标系转换

要使用Frenet坐标系进行运动规划，就需要将笛卡尔坐标系下的车辆状态转化为Frenet坐标系下的状态。由于公式太多，只能采用图片方式呈现后续内容。

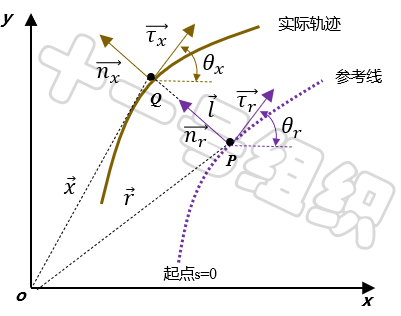
图3 Frenet坐标系和笛卡尔坐标系下的状态表示

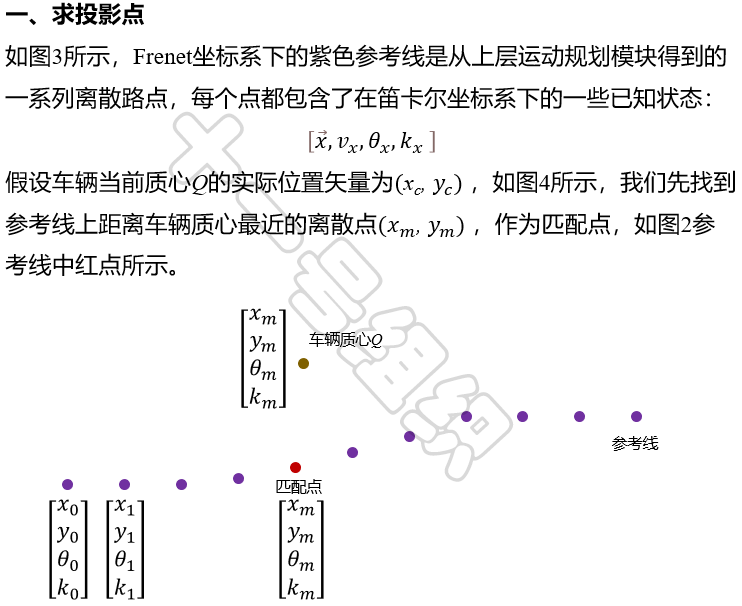
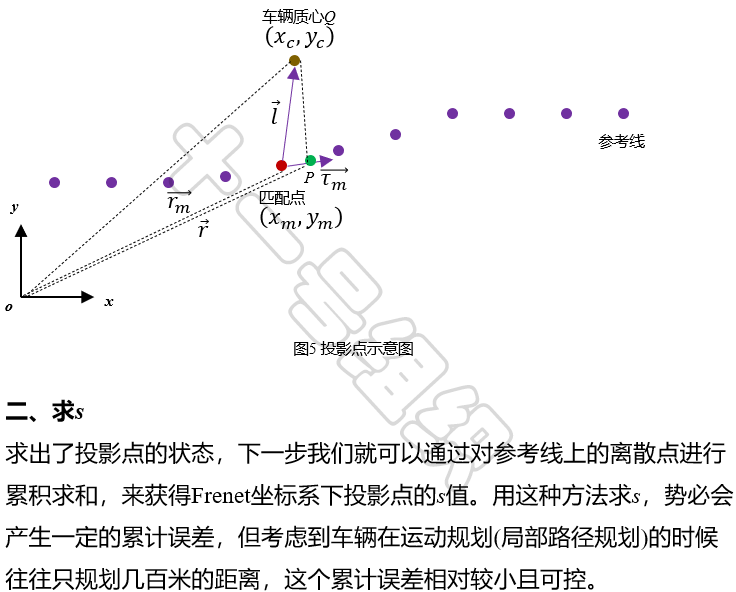
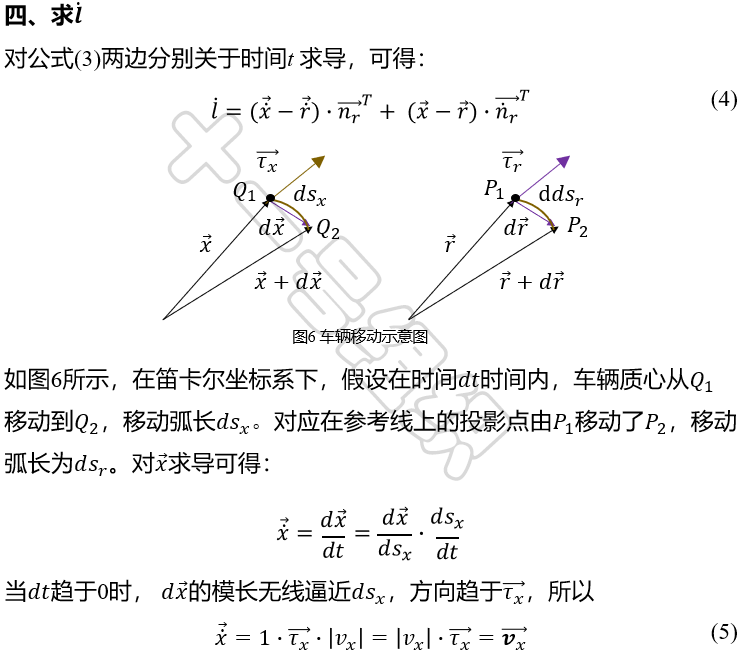
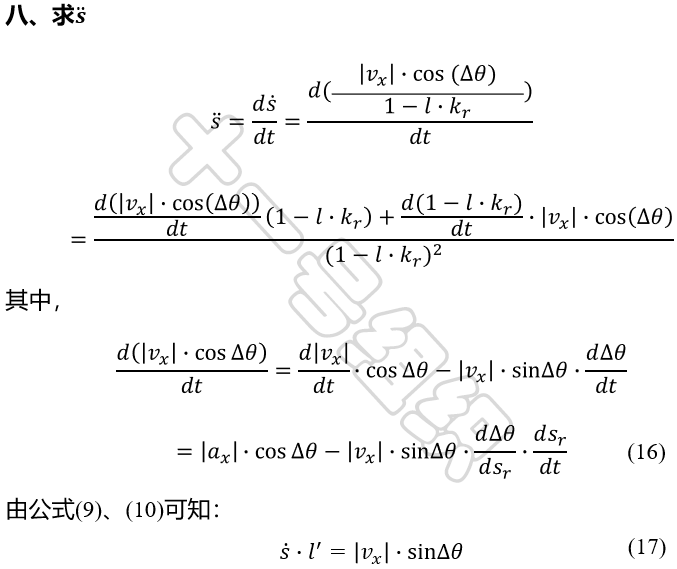
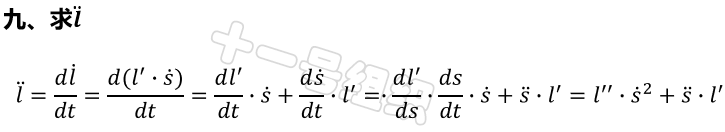
基于Frenet坐标系进行运动规划，将输出单独的横、纵向轨迹，而最终输出到自动驾驶车辆参考运动轨迹需要可直接被控制模块所应用，因此最后还需要把Frenet坐标系下得到的轨迹转化到一个全局笛卡尔坐标系中。逆过程过于简单，下面直接给出结论。

04写在最后

Frenet坐标系的熟练掌握，应该是规划控制入门的第一课，也是开启你自动驾驶混乱时代的第一课。

审核编辑 ：李倩