多面体模型的基本概念

编译器中的多面体模型（polyhedral model）是一种高效的程序优化技术，它将复杂的循环依赖关系映射到高维几何空间，从而在编译阶段实现对计算任务的并行化和局部性优化。

通过构建和操作多面体表示能有效地调度指令和数据访问，以减少资源争用和缓存未命中德情况，从而提高程序执行的性能。

本文将介绍多面体编译技术的理论基础，并以发掘循环可并行部分为例子讲解。

将循环表示为线性不等式

首先我们来看一个常规的循环:

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    S[i][j] = .... 

我们先不关注循环内执行什么语句，而是关注迭代空间 i 和 j 以及迭代限制条件：

i >= 1
i < N
j >= 1
j < N

转换为等价形式：

i >= 1
i <= N - 1
j >= 1
j <= N - 1

再统一转换为 >= 0 约束：

i - 1 >= 0
-i + N - 1 >= 0
j - 1 >= 0
-j + N - 1 >= 0

这样就将循环迭代空间表示成了一组线性不等式，然后矩阵形式表达如下：

这一组线性不等式其实就定义了二维空间上的一个矩形：

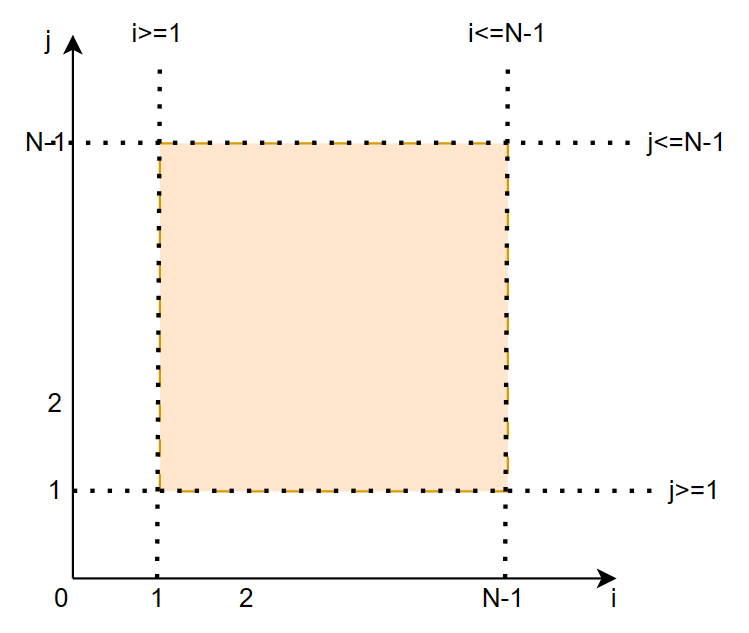
我们再来看一个例子，

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    if (i <= N - j + 1)
      S[i][j] = .... 

这个循环相比上面的循环就是多了一个约束条件 i <= N - j + 1 也就是 j <= -i + N + 1，也就是在上面坐标轴上再加一条线：

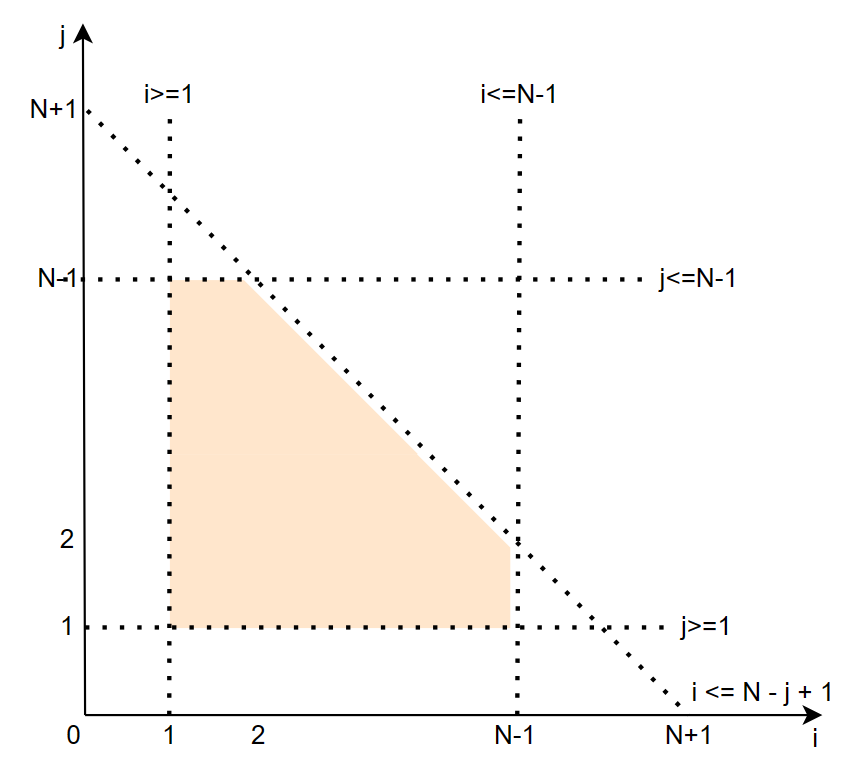
这样就很清楚了，这些约束的交集对应了二维空间上的一个多面体（polyhedron），同理可得如果是三层循环空间，那就是对应了三维空间上的一个多面体，每个约束条件对应一个二维平面，而在 n 维空间上就是一个超平面了。

数据依赖距离向量的定义

接着我们来介绍怎么分析循环中的数据依赖，多面体模型中的数据依赖描述了在循环结构中，不同迭代之间因数据访问而产生的依赖关系。

而对于循环嵌套内的依赖关系，可以用距离向量来描述相对执行顺序。

比如对于以下循环：

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    A[i][j] = A[i-1][j] + A[i][j-1];  

在当前次 (i 和 j) 迭代中需要往 A[i][j] 中写入数据，然后需要读取 A[i-1][j] 和 A[i][j-1] 的内容也就是循环维度 i 和 j 的前一次迭代 i-1 和 j-1 需要写入的位置，所以这就引入了一个先写然后再读取的数据依赖。

然后我们定义距离向量如下，向量的值大小表示了在对应循环维度上依赖的上一次迭代的距离：

• A[i][j] -> A[i-1][j] 的距离向量为 [i - (i -1 ), j - j] = [1, 0]
• A[i][j] -> A[i][j-1] 的距离向量为 [i - i, j - (j - 1)] = [0, 1]

矩阵形式表示：

 

能否简单从距离向量看出循环能否并行呢？

以下讨论均假设循环都是正向且迭代步长均为1，且迭代空间为常规的整数，且不保证结论能推广。

对于该循环

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    A[i][j] = A[i-1][j] + A[i][j-1];  

其距离向量为：

 

分析第一行可以看到i 循环维度的上，依赖了前一次迭代的计算值，所以可以知道在 i 循环上无法并行。

而分析第二行依赖，j 循环维度也依赖了前一次迭代的计算值，所以可以知道在 j 循环上也无法并行。

又比如对于循环

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    A[i][j] = 0;  

其距离向量为 [0]。

循环维度 i 和 j 对于前面的循环没有任何依赖，所以能将两个循环合并为一个然后并行运行。

又比如对于循环

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    A[i][j] = A[i][j-1];  

其距离向量为 [0, 1]。循环维度 i 无依赖可以在该维度上并行，但是在 j 维度上有依赖无法并行。

又比如对于循环

for (int i = 1; i < N; ++i)
  for (int j = 1; j < N; ++j)
    A[i][j] = A[i-1][j] + A[i-1][j-1];  

其距离向量为：

 

两个依赖的循环维度 i 都是大于0，所以在 i 维度无法循环，但是在 j 维度却可以并行。所以只要第一列都大于0，则不用分析第二维了，第二维是一定可以并行的。

有些循环的距离向量没法直接看出来，比如经典的矩阵乘法：

for (int i = 0; i < N; ++i)
  for (int j = 0; j < N; ++j)
    for (int k = 0; k < N; ++j)
      C[i][j] = C[i][j] + A[i][k] * B[k][j];

这里在循环维度 k 上有个隐式的依赖，当前迭代(i', j', k') 的 C[i'][j'] 计算依赖于上一次迭代 (i', j', k'-1) 计算得到的 C[i'][j']，所以距离向量为 [0, 0, k-(k'-1)=1]，所以在k 维度上无法并行。

对循环做变换

多面体模型中对循环优化是通过对循环迭代空间做仿射变换实现的，下面我们介绍三种简单的变换，交换和倾斜。

以二层循环为例:

for (int i = 1; i <= 2; ++i)
  for (int j = 1; j <= 3; ++j)
    S[i][j] = ...  

对应的每一次迭代的执行顺序如下图，图中的圆型就对应每一次的迭代，序号就是原始执行顺序：

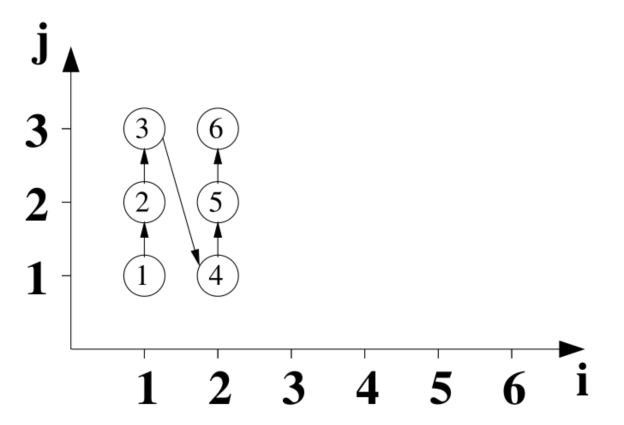
假设变换后的循环维度分别是 i' 和 j'。

循环交换

对应的变换矩阵如下：

 

变换过程如下：

 

对应的循环就变为：

for (int j = 1; j <= 3; ++j)
  for (int i = 1; i <= 2; ++i)
    S[i][j] = ...  

对应的迭代执行顺序如下：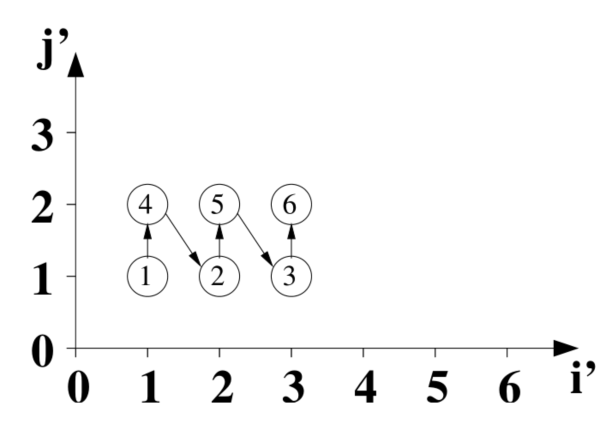

图中圆型的序号为变换前的原始执行顺序。

第一个执行的坐标是 (i'=1, j'=1)，对应原始坐标是 (i=1, j=1)，对应圆型 1。

第二个执行的坐标是 (i'=1, j'=2)，对应原始坐标是 (i=2, j=1)，对应圆型 4。

第三个执行的坐标是 (i'=2, j'=1)，对应原始坐标是 (i=1, j=2)，对应圆型 2。

其他以此类推

循环反转

对应的变换矩阵如下，假设就对循环 i 做反转：

 

变换过程如下：

 

对应的循环就变为：

for (int i = -1; i >= -2; --i)
  for (int j = 1; j <= 3; ++j)
    S[i+3][j] = ...  

对应的迭代执行顺序如下：

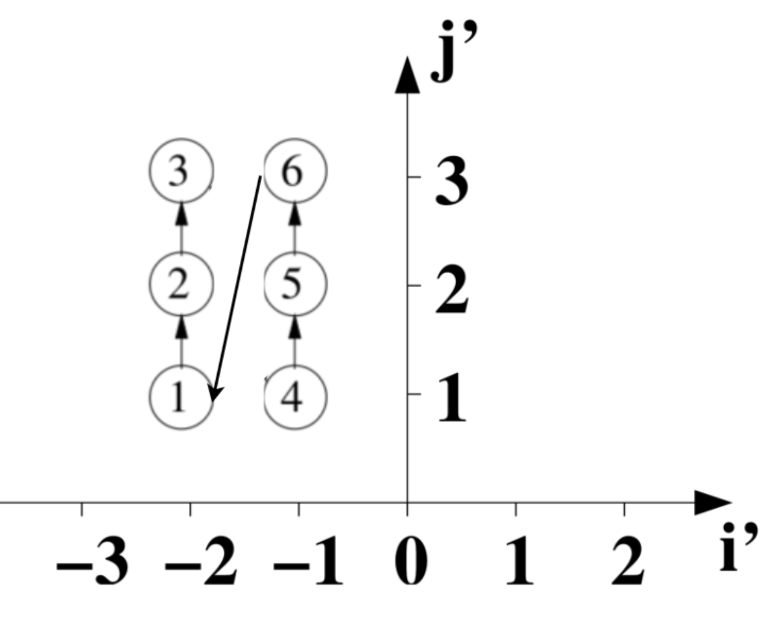
图中圆型的序号为变换前的原始执行顺序。

第1个迭代 (i'=-1, j'=1) 对应原始坐标 (i=2, j=1) ，对应原始循环的圆型 4 。

第4个迭代 (i'=-2, j'=1) 对应原始坐标 (i=1, j=1) ，对应原始循环圆型 1 。

循环倾斜

对应的变换矩阵如下：

 

变换过程如下：

 

对应的循环就变为：

for (int d = 2; d <= 5; ++d)
  for (int j = max(1, d - 2); j <= min(3, d - 1); ++j)
    int i = d - j;
    S[i][j] = ...  

对应的迭代执行顺序如下：

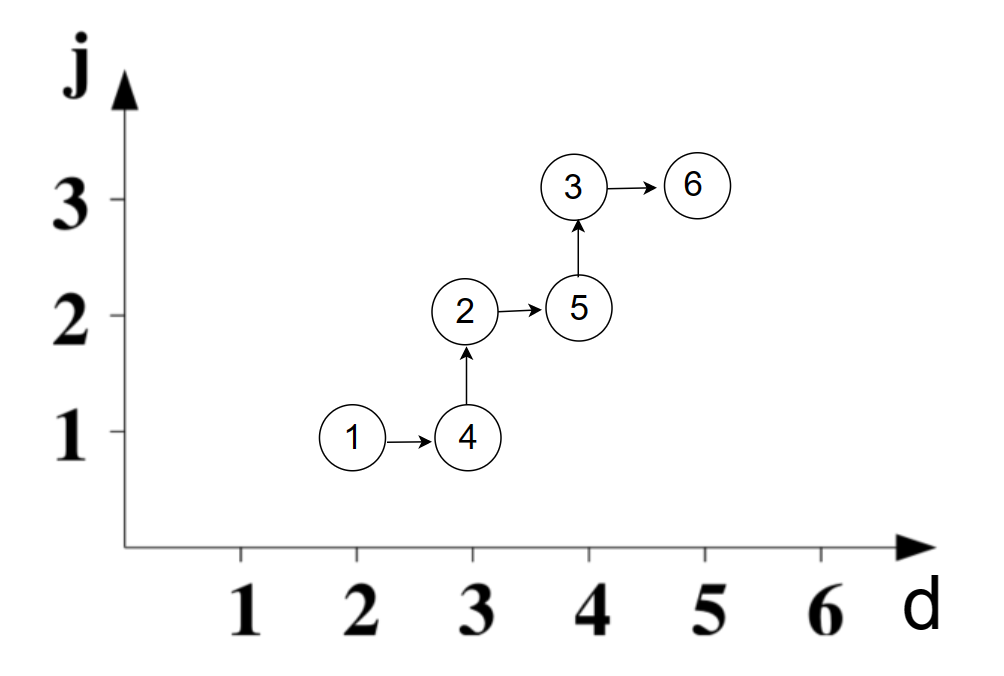
图中圆型的序号为变换前的原始执行顺序。

第1个迭代 (d=2, j=1) 对应原始坐标 (i=1, j=1) ，对应原始循环的圆型 1 。

第2个迭代 (d=3, j=1) 对应原始坐标 (i=2, j=1) ，对应原始循环圆型 4 。

第3个迭代 (d=3, j=2) 对应原始坐标 (i=1, j=2) ，对应原始循环圆型 2 。

第4个迭代 (d=4, j=2) 对应原始坐标 (i=2, j=2) ，对应原始循环圆型 5 。

第5个迭代 (d=4, j=3) 对应原始坐标 (i=1, j=3) ，对应原始循环圆型 3 。

第6个迭代 (d=5, j=3) 对应原始坐标 (i=2, j=3) ，对应原始循环圆型 6 。

如何将串行执行的循环转换为可并行执行

以下面的循环为例：

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) {
        A[i][j] = A[i-1][j] + A[i][j-1];
    }
}

分析上其数据依赖分析可得其距离向量：

 

可知该循环在 i 和 j 维度上都无法并行执行。

接下来尝试对循环空间 i 和  j 做仿射变换，我们采用倾斜变换，其实这个是很经典的一个并行方法了，称之为对角线变换。

具体到多面体编译技术的代码的实现，是怎么自动找到这个变换的过程我还没完全弄懂，所以假设我们现在知道了是直接应用倾斜变换：

 

代码变为：

for (int d = 2; d <= 2 * N; ++d) {
    for (int j = max(1, d - N); j <= min(N, d - 1); ++j) {
        int i = d - j;
        A[i][j] = A[i-1][j] + A[i][j-1];
    }
}

接着分析数据依赖矩阵，这时候 A[i][j]= A[d-j][j] 的计算都只依赖于循环 d 前一次迭代的计算而循环 j 维度上没有数据依赖，所以依赖矩阵为：

 

从依赖矩阵可知，变换后的循环可以在 j 循环维度上做循环。

上面的文字解释可能有些抽象我们画图来辅助解释，假设循环上界 N=5，则原始的循环迭代空间如下图所示：

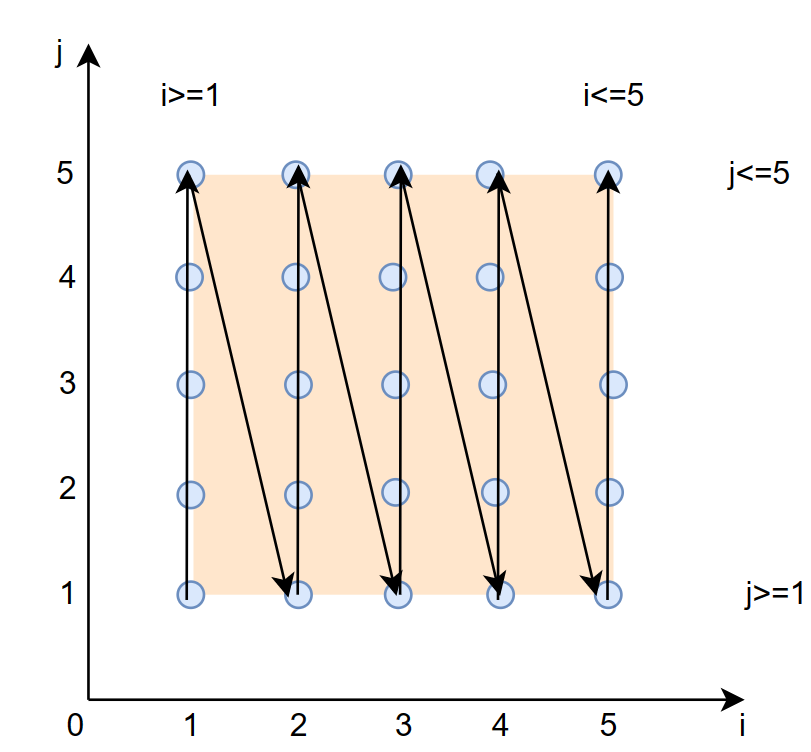
黑色实线箭头表示每个计算 A[i][j] 的计算顺序。

数据依赖关系如下：

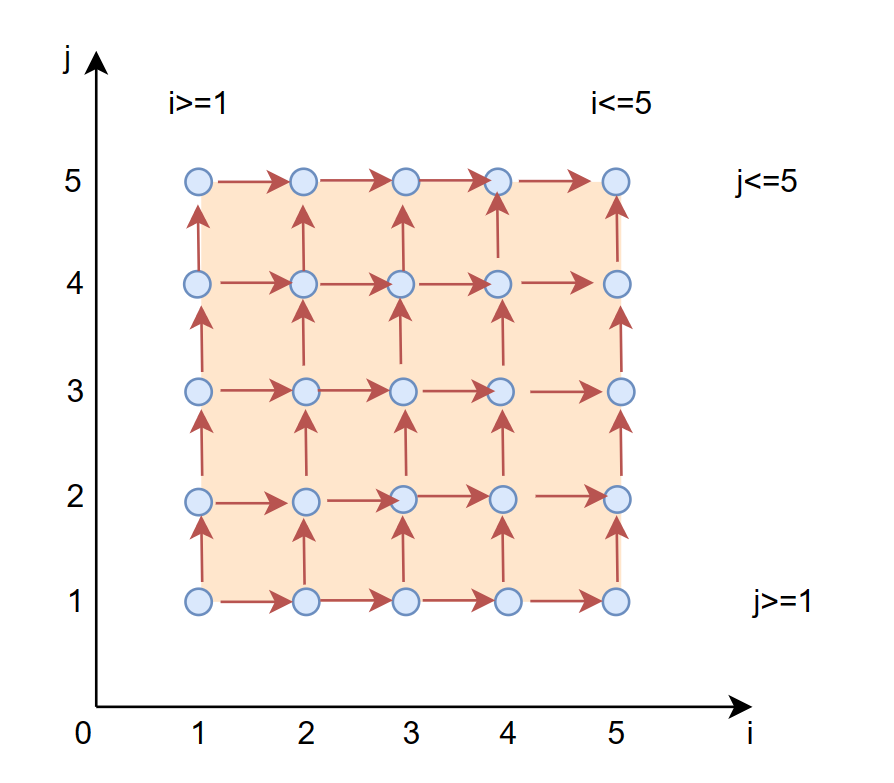
红色箭头表示数据依赖。

则经过倾斜变换后的循环迭代空间如下：

for (int d = 2; d <= 2 * 5; ++d) {
    for (int j = max(1, d - 5); j <= min(5, d - 1); ++j) {
        int i = d - j;
        A[i][j] = A[i-1][j] + A[i][j-1];
    }
}

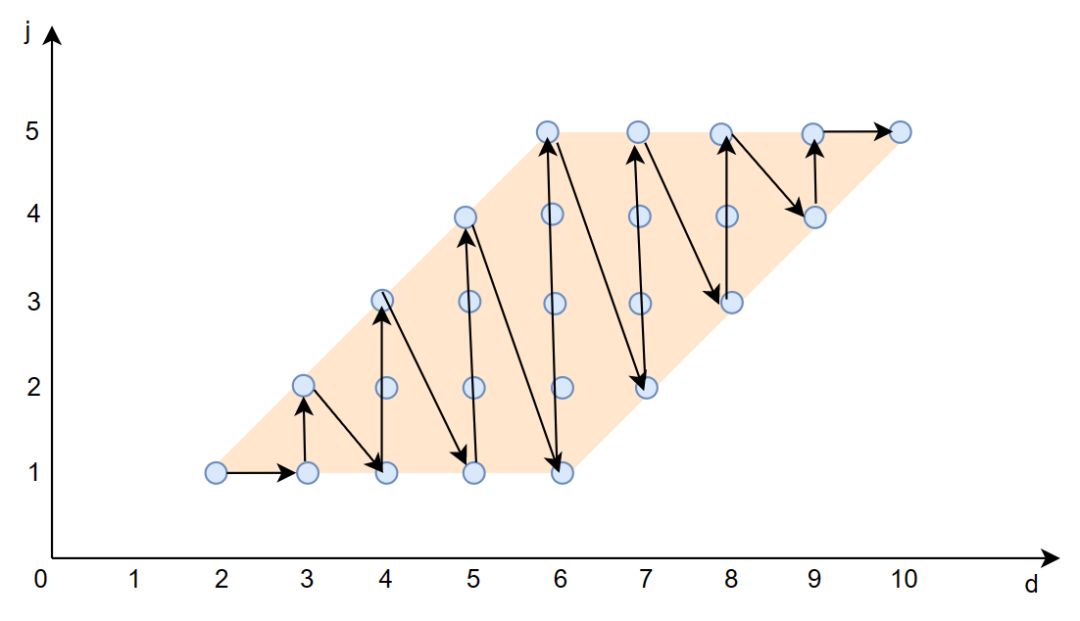
其实就是对应于原始空间上，按照对角线的顺序去遍历。

数据依赖如下：

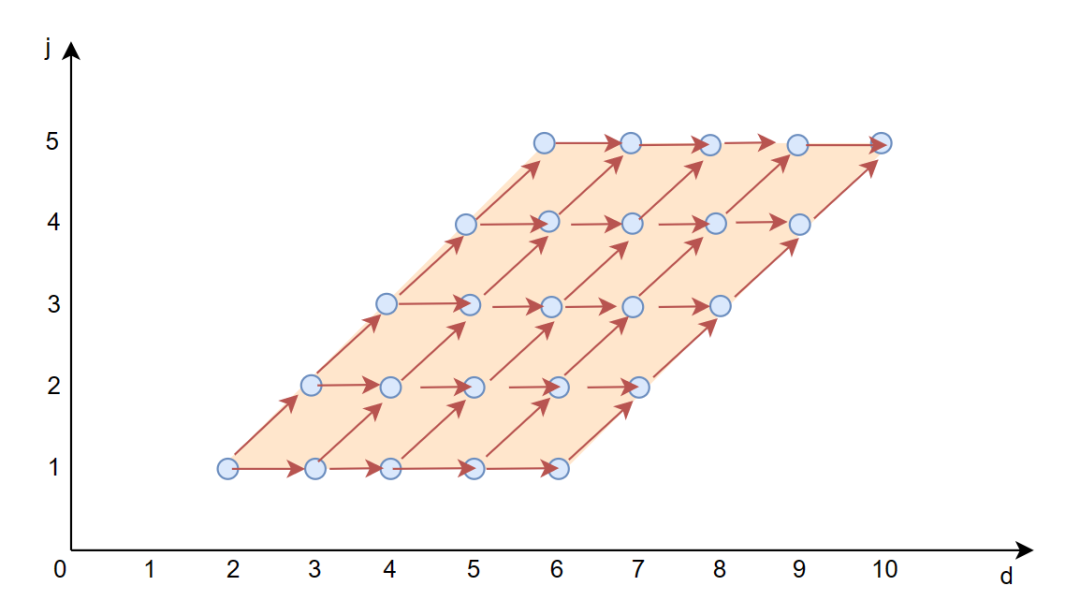
从数据依赖上看，可以看到变换后在 j 维度上没有数据依赖所以可以并行执行。

最后在 j 维度上加上 omp 并行：

for (int d = 2; d <= 2 * 5; ++d) {
    #pragma omp for 
    for (int j = max(1, d - 5); j <= min(5, d - 1); ++j) {
        int i = d - j;
        A[i][j] = A[i-1][j] + A[i][j-1];
    }
}

后记

这篇文章中对于多面体模型有并不少是个人理解，不一定准确。多面体编译技术个人感觉很复杂，在阅读相关文献和书籍的时候，还需要去搜过相关前置知识才能看懂大概。

而这篇学习笔记也仅仅是介绍了一些基本的入门概念，多面体编译技术能做的事情并不仅仅局限于本文所介绍的循环变换发掘可并行部分，感兴趣的读者可以阅读参考资料。

审核编辑 ：李倩