光通信的最强进阶科普2

█ 光相位调制

接下来，我们讲讲光相位调制。（敲黑板，这部分可是重点！）

其实刚才我们已经讲到了相位，不过那个是借助相位差产生幅度差，依旧属于幅度调制。

首先，我们回忆一下高中（初中？）的数学知识——虚数和三角函数。

在数学中，虚数就是形如a+b*i的数。实部a可对应平面上的横轴，虚部b与对应平面上的纵轴，这样虚数a+b*i可与平面内的点(a,b)对应。

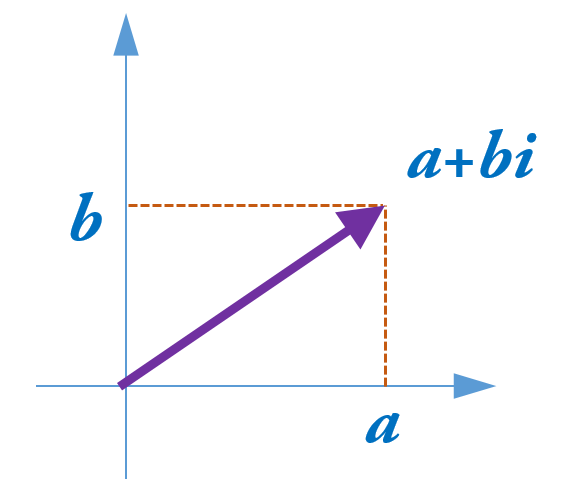
大家应该还记得，坐标轴其实是可以和波形相对应的，如下：

波形，其实又可以用三角函数来表示，例如：

多么优美，多么妖娆~

X = A * sin（ωt+φ）= A * sinθ

Y = A * cos（ωt+φ）= A * cosθ

ω是角速度，ω=2πf，f是频率。

φ是初相位，上图为0°。

还记得不？把A看出幅度，把θ看成相位，就是电磁波的波形。

θ=0°，sinθ=0

θ=90°，sinθ=1

θ=180°，sinθ=0

θ=270°，sinθ=-1

好了，基础知识复习完毕，现在进入正文。

首先，我们介绍一下， 星座图 。

其实刚才介绍MZ调制器相位变化的时候，已经看到了星座图的影子。下面这几张图图，都属于星座图。图中的黑色小点，就是星座点。

大家会发现，星座图和我们非常熟悉的纵横坐标系很像。是的，星座图里的星座点，其实就是振幅E和相位Ф的一对组合。

就要提出 I/Q调制 （不是智商调制啊!）。

I，为in-phase，同相或实部。Q，为quadrature phase，正交相位或虚部。所谓正交，就是相对参考信号相位有-90度差的载波。

我们继续来看。

在星座图上，如果幅度不变，用两个不同的相位0和180°，表示1和0，可以传递2种符号，就是 BPSK （Binary Phase Shift Keying，二进制相移键控）。

BPSK

BPSK是最简单最基础的PSK，非常稳，不容易出错，抗干扰能力强。但是，它一个符号只能传送1个比特，效率太低。

于是，我们升级一下，搞个 QPSK （Quadrature PSK，正交相移键控）。

QPSK，是具有4个电平值的四进制相移键控（PSK）调制。它的频带利用率，是BPSK的2倍。

图片来自是德科技

随着进制的增加，虽然频带利用率提高，但也带来了缺点——各码元之间的距离减小，不利于信号的恢复。特别是受到噪声和干扰时，误码率会随之增大。

为解决这个问题，我们不得不提高信号功率（即提高信号的信噪比，来避免误码率的增大），这就使功率利用率降低了。

有没有办法，可以兼顾频带利用率和各码元之间的距离呢？

有的，这就引入了 QAM （Quadrature Amplitude Modulation，正交幅度调制）。

QAM的特点，是各码元之间不仅相位不同，幅度也不同。它属于相位与幅度相结合的调制方式。

大家看下面这张动图，就明白了：

Amp，振幅。Phase，相位。

其实，QPSK就是电平数为4的QAM。上图是16QAM，16个符号，每个符号4bit（0000，0001，0010等）。

64QAM的话，64个符号（2的n次方，n=6），每个符号6bit（000000，000001，000010等）。

QPSK这种调制，到底是怎么捣鼓出来的呢？

我们可以看一个通过MZ调制器捣鼓QPSK的图片：

图片来自是德科技

在发射机中，电比特流被一个多路复用器分成信号的I和Q部分。这两部分中的每一部分都直接调制MZ调制器一只臂上的激光信号的相位。另一个MZ调制器把较低的分支相移π⁄2。两个分支重组后，结果是一个QPSK信号。

高阶QAM的调制难度更大。限于篇幅，下次我再专门给大家解释。

此前介绍无线通信调制的时候，说过5G和Wi-Fi 6都在冲1024QAM。那么，光通信是不是可以搞那么高阶的QAM呢？

不瞒您说，还真有人这么干了。

前几年，就有公司展示了基于先进的星系整形算法和奈奎斯特副载波技术的1024QAM调制，基于66Gbaud波特率，实现了1.32Tbps下的400公里传输，频谱效率达到9.35bit/s/Hz。

不过，这种高阶调制仍属于实验室阶段，没有商用（也不知道有没有可能商用）。目前实际应用的，好像没有超过256QAM。

高阶QAM虽然带来了传输速率的大幅提升，但对元器件性能要求很高，对芯片算力的要求也高。而且，如果信道噪声或干扰太大，还是会出现刚才所说的高误码率问题。

1024QAM，密集恐惧症的节奏

在相同的30G+波特率下，16QAM的光信噪比（OSNR）比QPSK高出约5dB。随着星座中星座点个数的增加，16QAM的OSNR将呈指数增长。

因此，16QAM或更高阶QAM的传输距离将被进一步限制。

为了进一步榨干光纤通信的带宽潜力，厂商们祭出了新的大杀器，那就是—— 相干光通信 。下期，小枣君将详细给大家介绍。

**█ **PAM4和偏振复用

文章的最后，再说说两个“翻倍”技术——PAM4和PDM偏振多路复用。

先说PAM4。

在PAM4之前，我们传统使用的都是NRZ。

NRZ，就是Non-Return-to-Zero的缩写，字面意思叫做“不归零”，也就是不归零编码。

采用NRZ编码的信号，就是使用高、低两种信号电平来表示传输信息的数字逻辑信号。

NRZ有单极性不归零码和双极性不归零码。

单极性不归零码，“1”和“0”分别对应正电平和零电平，或负电平和零电平。

单极性不归零码

双极性不归零码，“1”和“0”分别对应正电平和等效负电平。

双极性不归零码

所谓“不归零”，不是说没有“0”，而是说每传输完一位数据，信号无需返回到零电平。（显然，相比RZ，NRZ节约了带宽。）

在光模块调制里面，我们是用激光器的功率来控制0和1的。

简单来说，就是发光，实际发射光功率大于某门限值，就是1。小于某门限值，就是0。

传输011011就是这样：

NRZ调制

后来，正如前文所说，为了增加单位时间内传输的逻辑信息，就搞出了PAM4。

PAM4，就是4-Level Pulse Amplitude Modulation，中文名叫做四电平脉冲幅度调制。它是一种高级调制技术，采用4个不同的信号电平来进行信号传输。

还是传输011011，就变成这样：

PAM4调制

这样一来，单个符号周期表示的逻辑信息，从NRZ的1bit，变成了2bit，翻了一倍。

NRZ VS PAM4 （右边是眼图）

那么问题来了，如果4电平能够翻一倍，为啥我们不搞个8电平、16电平、32电平？速度随便翻倍，岂不爽歪歪？

答案是不行。

主要原因，还是在于激光器的技术工艺。实现PAM4，需要激光器能够做到对功率的精确控制。

如果工艺不OK，搞更高位数电平，就会造成很高的误码率，无法正常工作。即便是PAM4，如果信道噪声太大，也是不能正常工作的。

什么是PDM偏振多路复用呢？

PDM偏振多路复用，就是Polarization Division Multiplexing。

不知道大家有没有看过我之前写过的关于天线的文章。天线里面，有一个双极化的概念，在空间上，把电磁波“转动”90度，就可以实现两个独立的电磁波传输。

天线的双极化

偏振复用的道理，其实也差不多。它利用光的偏振维度，在同一波长信道中，通过光的两个相互正交偏振态，同时传输两路独立数据信息，以此达到提升系统总容量的目的。

它等于实现了双通道传输，和PAM4一样，翻了一倍。

PDM偏振复用，X偏振和Y偏振，各自独立

图片来自是德科技

好啦，以上就是今天文章的全部内容。感谢大家的耐心观看，我们下期介绍相干光通信，不见不散哟！