

系统稳定性分析以及波特图的解读
描述
Bode图基本概念介绍 当今社会各种各样的电子产品已经是我们生活不可分割的一部分,在各类电子产品中,我们面对不同客户的供电需求也不尽相同,该如何保证电源芯片更好的与客户产品进行兼容并稳定运行呢?相信各位工程师朋友都听过小信号测试,作为一种应用十分广泛的系统稳定性的判定依据,我们是如何通过测试结果来分析系统性能呢?本文将带大家揭开小信号测试的“神秘面纱”。 Bode图是测试结果波形的载体,这是一种简便并且准确的绘制系统增益及相位的图,它被广泛的应用于实际工作中,波特图一般是由两张图片组合而成:G(jw)的幅值(以分贝dB表示)-频率(以对数标度)对数坐标图,其上画有对数幅频曲线来反映系统的幅频特性,G(jω)的相角-频率(以对数标度)对数坐标图,其上画有相频特性来反映系统的相频特性,通过两者相结合来对系统的性能进行评估。对于两张图而言其横轴频率以对数尺度十倍频程(log scale)表示,这一点是不同于一般图表的等间距计量,比如频率刻度为是10、100、1000、10^4,每一小格代表不同的频率跨度。这样一来可以将很宽范围的信号波形纳入一张表格中。对于幅频相位图而言,其纵坐标的对数幅值的标准表达式为20 lg|G(jω)|,对于相频相位图而言其纵坐标单位为度。如下图所示即为实际测量中所作的一组波特图。
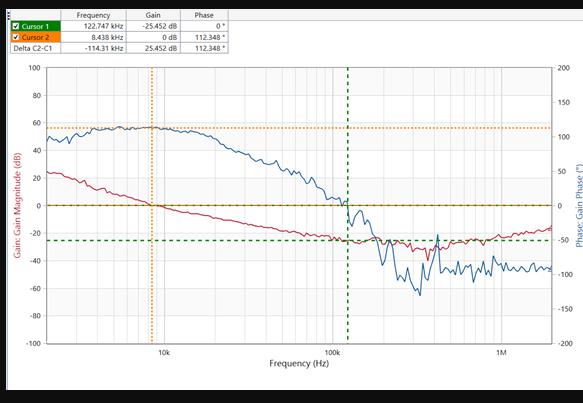
2.小信号测试原理及bode图中关注的指标信号测试原理 :对于电源系统而言我们常在输出反馈电阻上串入一个阻值很小的电阻(10Ω),在串入的电阻两端通过小信号测试仪器将一组信号注入环路中,我们再将注入环路的信号接收,将其绘制在波德图上,通过分析初始小信号在经过给定系统后的输出信号的相频或者幅频特性来判断系统是否稳定。例如一个Asin(ω t ) 的信号进入系统后振幅变原来的k 倍,相位落后原信号Φ,则其输出信号则为( Ak )sin(ω t −Φ),其中的k 和Φ都是频率的函数。那么输出信号的特性就可以通过波特图来显示出来。我们通过对输出信号的分析来对系统的稳定性进行判断。
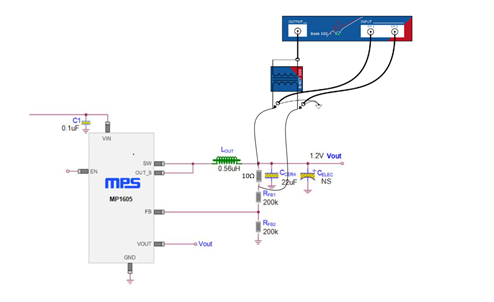
如何从波特图反映系统的稳定性?这里就要介绍奈氏判据:作为自动控制理论中一种应用十分广泛的系统研究理论,它是通过系统的开环特性来研究闭环的性能,利用复变函数中的辐角原理建立判别系统稳定与否的一种方法。其中我们所说的通过相位裕量、幅值裕量、截止频率来判别系统稳定性的结论均是由奈氏判据推导而来。由奈氏判据可知**:** 幅频图纵轴0分贝以下具有正增益裕度、属稳定区,反之属不稳定区。频图纵轴-180度以上具有正相位裕度、属稳定区,反之为不稳定区。接下来结合波特图介绍一下我们常用来分析系统稳定性的一些概念:相角裕度:当环路增益的幅频特性曲线过零的频率点,对应相频特性曲线距离-180°的角度差。PM=∠T(jω)-(-180°) 可以理解为如果相位再滞后PM角度后,系统的相角会降 低到-180°系统就会落入到不稳定区系统将会由负反馈变成正反馈,从而导致系统不稳定。通常我们要求系统的相角至少在45°以上。幅值裕度:当环路增益的相频特性曲线经过180°的频率点时,对应的幅频特性曲线衰减的倍数 AM=20 log〖1/(T(jω))〗 (dB)可以理解为如果幅值再增加AM倍后,系统的幅值会增加到单位1,从而导致系统不稳定。一般我们要求AM<-10dB带宽:幅频相位曲线穿越过零点时对应的频率为带宽,带宽越宽,系统对于扰动的响应越及时,因此扰动对于输出的影响就越小。对我们系统而言如果系统的带宽高,则可以动态性能好,但此时会影响幅值裕量和相位裕量,影响系统的稳定性能。所以,一个系统的带宽需要高,但不能太高。通常我们要求带宽位于1/20 Fsw。直流增益:如果给定信号是直流信号,则为使得输出直流信号无稳态误差,则需要使得环路增益在DC为无穷大。伯德图上需要环路增益在低频段至少-20dB/dec下降即传递函数具有位于原点的极点。
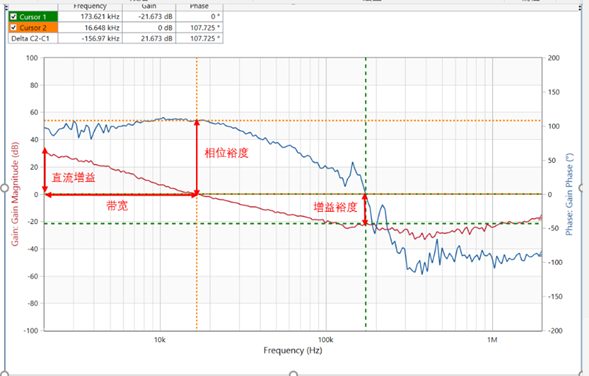
- 三段法判定系统性能的分析
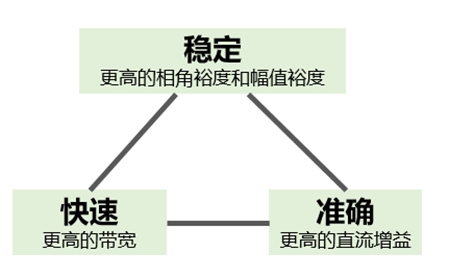
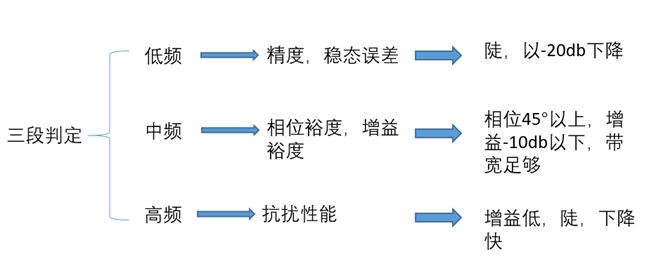
对于一张波特图而言我们依照频率将其分为低频,中频,高频三个不同分段,其不同频段着重反映着系统的不同性能,所以我们也可以用三段法对系统的性能有一个很好的评估。
低频段: 反映系统的稳态精度和响应速度。
中频段: 反映了系统的稳定性和动态性能。
高频段: 反映了系统的抗噪声能力。
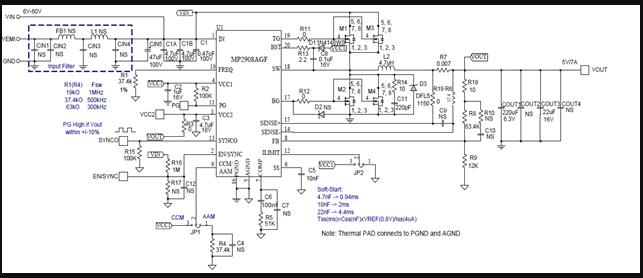
- 实际应用案例的环路调试 经过前文的分析,我们已经知道如何通过波特图来大致判断一个系统的性能,对于一个环路而言,我们在实际操作中该调节什么参数才能使我们获得理想的参数呢?在MPS芯片集成化越来越高的今天,我们只需要对外围前馈电容和RT电阻进行调节,便可以使我们获得理想的系统带宽,增益,相位裕度等参数。接下来以实际调试为例,我们看看前馈电容是如何影响我们的bode图呢? 从理论上分析增加一颗前馈电容,相当于引入了一对零点和极点,增大前馈电容会使的我们bode图的带宽右移。以MP2908A的调试为例工作条件24V→3.3V@6A,如下图即为实验的原理图,在此基础上Comp参数为:51K 100nF;前馈分别为:0pF 和27pF, 我们可以看到带宽明显得到了改善,系统的动态性能也得到了优化。
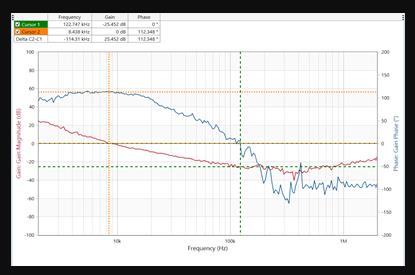
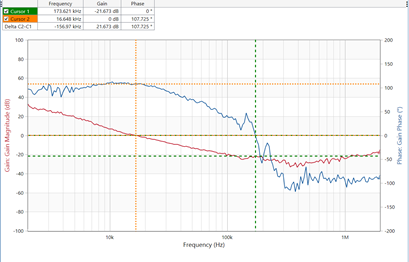
-
buck电路的稳定性分析方法2024-11-21 2547
-
TINA可以进行运放的稳定性分析吗?2024-09-04 287
-
使用TINA进行稳定性分析时用几种不同方式出现了较大的相位裕度差异,为什么?2024-08-21 425
-
关于电源/负载电路组合的稳定性分析2021-05-11 2337
-
开关电源环路稳定性分析2020-05-31 3933
-
一类离散时滞切换系统的稳定性分析_曹莹2017-03-15 803
-
线性定常系统的瞬态响应和稳定性分析2016-09-01 1860
-
运放稳定性分析详解(五)2016-08-08 911
-
Buck变换器稳定性分析2016-07-25 924
-
矩阵变换器_永磁同步电机驱动系统静态稳定性分析2016-05-04 1132
-
运放稳定性分析2016-02-19 975
-
一类线性时变系统线性化稳定性分析方法的讨论2016-01-07 590
-
LDO稳定性分析2011-11-01 863
-
频率响应法-相对稳定性分析2009-07-27 3448
全部0条评论

快来发表一下你的评论吧 !


