

50Ω阻抗问题详解及射频电路设计中的阻抗匹配
描述
为什么很多射频系统或者部件中,很多时候都是用50欧姆的阻抗。
有时候这个值甚至就是PCB板的缺省值 ,为什么不是60或者是70欧姆呢? 这个数值是怎么确定下来的,背后有什么意义? 本文为您打开其中的奥秘。
我们知道射频的传输需要天线和同轴电缆,射频信号的传输我们总是希望尽可能传输更远的距离,为了传输更远的距离,我们往往希望用很大的功率去发射信号便于覆盖更大的通信范围。 可是实际上,同轴电缆本身是有损耗的,和我们平常使用得导线一样,如果传输功率过大,导线会发热甚至熔断。 这样,我们就有一种期望,试图寻找一种能够传输大功率,同时损耗又非常小的同轴电缆。
大概在1929年,贝尔实验室做了很多实验,最终发现符合这种大功率传输,损耗小的同轴电缆其特征阻抗分别是30欧姆和77欧姆。 其中,30欧姆的同轴电缆可以传输的功率是最大的,77欧姆的同轴电缆传输信号的损耗是最小的。 30欧姆和77欧姆的算术平均值为53.5欧姆,30欧姆和77欧姆的几何平均值是48欧姆,我们经常所说的50欧姆系统阻抗其实是53.5欧姆和48欧姆的一个工程上的折中考虑,考虑最大功率传输和最小损耗尽可能同时满足。 而且通过实践发现,50欧姆的系统阻抗,对于半波长偶极子天线和四分之一波长单极子天线的端口阻抗也是匹配的,引起的反射损耗是最小的。
我们常见的系统中,比如电视TV和广播FM接收系统中,其系统阻抗基本上都是75欧姆,正是因为75欧姆射频传输系统中,信号传输的损耗是最小的,TV和广播FM接收系统中,信号的传输损耗是重要的考虑因素。 而对于带有发射的电台而言,50欧姆是很常见的,因为最大功率传输是我们考虑的主要因素,同时损耗也比较重要。 这就是为什么我们的对讲机系统中,经常看到的都是50欧姆的参数指标。
如果说阻抗匹配到50欧姆,从数学上,是可以严格做到的,但是实际应用中的任何元件,线路,导线都存在损耗,而且设计的任何系统部件都存在一定的射频带宽,所以匹配到50欧姆,工程上只要保证所有的带内频点落在50欧姆附近即可。 在Smith圆图上来看,就是尽可能趋近于圆图的圆心即可,确保带内的射频传输信号尽可能没有反射损耗,获得最大程度的能量传输。
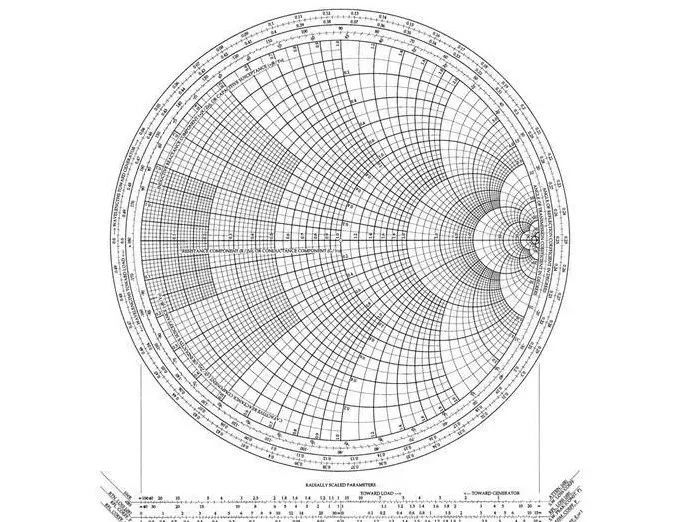
为什么大多数工程师喜欢用 50 欧姆作为 PCB 的传输线阻抗(有时候这个值甚至就是 PCB 板的缺省值) ,为什么不是 60 或者是 70 欧姆呢?
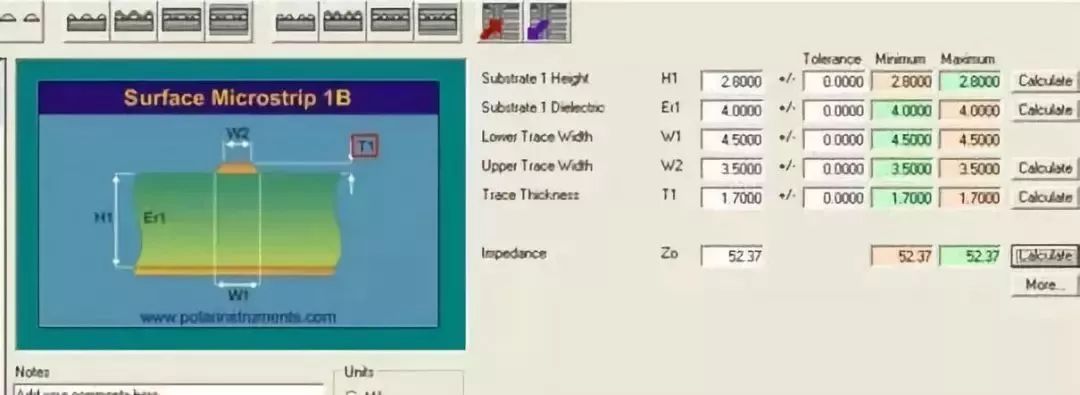
对于宽度确定的走线,3 个主要的因素会影响 PCB 走线的 阻抗。 首先,是 PCB 走线近区场的 EMI(电磁干扰)和这个走线距参考平面的高度是成一定的比例关系的,高度越低意味着辐射越小。 其次,串扰会随走线高度有显著的变化,把高度减少一半,串扰会减少到近四分之一。 最后,高度越低阻抗越小,不易受电容性负载影响。 所有的三个因素都会让设计者把走线尽量靠近参考平面。 阻止你把走线高度降到零的原因是,大多数芯片驱动不了阻抗小于 50 欧姆的传输线。 (这个规则的特例是可以驱动 27 欧姆的Rambus,以及 National 的的 BTL 系列,它可以驱动 17 欧姆)并不是所有的情况都是用50欧姆最好。 例如,8080 处理器的很老的 NMOS 结构,工作在 100KHz,没有 EMI,串扰和电容性负载的问题,它也不能驱动 50 欧姆。 对于这个处理器来说,高的阻抗意味着低功耗,你要尽可能的用细的,高的这样有高阻抗的线。 纯机械的角度也要考虑到。 例如,从密度上讲,多层板层间距离很小,70 欧姆阻抗所需要的线宽工艺很难做到。 这种情况,你应该用 50 欧姆,它的线宽更加宽,更易于制造。
同轴电缆的阻抗又是怎么样的呢? 在 RF 领域,和 PCB 中考虑的问题不一样,但是RF 工业中同轴电缆也有类似的阻抗范围。 根据 IEC 的出版物(1967年),75 欧姆是一个常见的同轴电缆(注:空气作为绝缘层)阻抗标准,因为你可以和一些常见的天线配置相匹配。 它也定义了一种基于固态聚乙烯的 50 欧姆电缆,因为对于直径固定的外部屏蔽层和介电常数固定为 2.2(固态聚乙烯的介电常数)的时候,50 欧姆阻抗趋肤效应损耗最小。
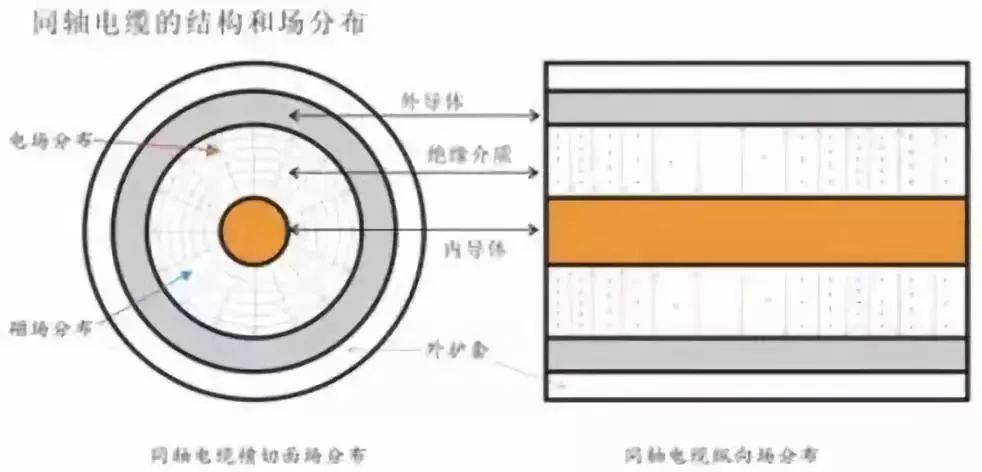
你可以从基本的物理学来证明 50 欧姆是最好的,电缆的趋肤效应损耗 L(以分贝做单位)和总的趋肤效应电阻 R(单位长度)除以特性阻抗 Z0 成正比。 总的趋肤效应电阻 R 是屏蔽层和中间导体电阻之和。 屏蔽层的趋肤效应电阻在高频时,和它的直径d2 成反比。 同轴电缆内部导体的趋肤效应电阻在高频时,和他的直径 d1 成反比。 总共的串联电阻 R,因此和(1/d2 +1/d1)成正比。 综合这些因素,给定 d2 和相应的隔离材料的介电常数 ER,你可以用以下公式来减少趋肤效应损耗。
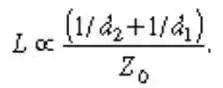
在任何关于电磁场和微波的基础书中,你都可以找到 Z0 是 d2,d1 和 ER(博主注:绝缘层的相对介电常数)的函数。
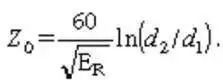
把公式 2 带入公式 1 中,分子分母同时乘以 d2,整理得到:
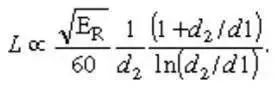
公式 3 分离出常数项(/60)*(1/d2),有效的项((1+d2/d1 )/ln(d2/d1 ))确定最小点。 仔细查看公式三公式的最小值点仅由 d2/d1 控制,和 ER 以及固定值 d2 无关。 以 d2/d1为参数,为 L 做图,显示 d2/d1=3.5911 时(注:解一个超越方程),取得最小值。 假定固态聚乙烯的介电常数为 2.25,d2/d1=3.5911 得出特性阻抗为 51.1 欧姆。 很久之前,无线电工程师为了方便使用,把这个值近似为 50 欧姆作为同轴电缆最优值。 这证明了在0 欧姆附近,L 是最小的。 但这并不影响你使用其他阻抗。 例如,你做一个 75 欧姆的电缆,有着同样的屏蔽层直径(注:d2)和绝缘体(注:ER),趋肤效应损耗会增加 12%。 不同的绝缘体,用最优 d2/d1 比例产生的最优阻抗会略有不同。
注:比如空气绝缘就对应 77 欧姆左右,工程师取值 75 欧姆方便使用。
其他补充:上述推导也解释了为什么 75 欧姆电视电缆切面是藕状空芯结构而 50 欧姆通信电缆是实芯的。 还有一个重要提示,只要经济情况许可,尽量选择大外径电缆(博主注:d2),除了提高强度外,更主要的原因是,外径越大,内径也越大(最优的径比d2/d1),导体的 RF 损耗当然就越小。
为什么 50 欧姆成为了射频传输线的阻抗标准? 一个最为流传的故事版本,来自于 Harmon Banning 的《电缆:关于 50 欧姆的来历可能有很多故事》。 在微波应用的初期,二次世界大战期间,阻抗的选择完全依赖于使用的需要. 对于大功率的处理,30 欧姆和 44 欧姆常被使用。 另一方面,最低损耗的空气填充线的阻抗是 93 欧姆。 在那些岁月里,对于很少用的更高频率,没有易弯曲的软电缆,仅仅是填充空气介质的刚性导管。 半刚性电缆诞生于 50 年代早期,真正的微波软电缆出现是大约 10 年以后了。 随着技术的进步,需要给出阻抗标准,以便在经济性和方便性上取得平衡。 在美国,50 欧姆是一个折中的选择; 为联合陆军和海军解决这些问题,一个名为 JAN 的组织成立了,就是后来的 DESC,由 MIL 特别发展的。 欧洲选择了 60 欧姆。
事实上,在美国最多使用的导管是由现有的标尺竿和水管连接成的,51.5 欧姆是十分常见的。 看到和用到 50 欧姆到 51.5 欧姆的适配器/转换器,感觉很奇怪的。 最终 50 欧姆胜出了,并且特别的导管被制造出来(也可能是装修工人略微改变了他们管子的直径)。 不久以后,在象 Hewlett-Packard 这样在业界占统治地位的公司的影响下,欧洲人也被迫改变了。 75 欧姆是远程通讯的标准,由于是介质填充线,在 77 欧姆获得最低的损耗。 93 欧姆一直用于短接续,如连接计算机主机和监视器,其低电容的特点,减少了电路的负载,并允许更长的接续; 感兴趣的读者可以查阅 MIT RadLab Series 的第 9 卷,里面有更详细的描述。
RF电路设计中的阻抗匹配
阻抗匹配是射频(RF)设计和测试的基本要求。 阻抗不匹配引起的信号反射会导致严重的问题。
当您处理由理想电源,传输线和负载组成的理论电路时,匹配似乎是一项微不足道的常识。
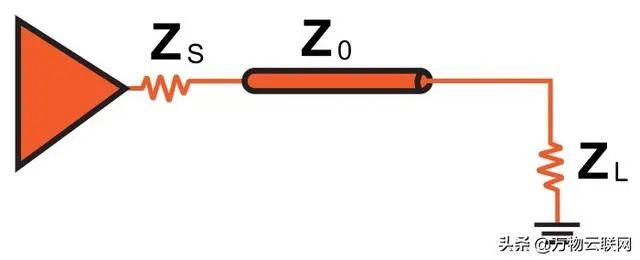
射频系统中的阻抗分布
假设负载阻抗ZL是固定的。 我们需要做的就是包括一个等于ZL的源阻抗(ZS),然后设计传输线,使其特性阻抗(Z0)也等于ZL。
但是,让我们暂时考虑一下在由众多无源元件和集成电路组成的复杂RF(射频)电路中实施此方案的难度。 如果工程师不得不根据选择的一个阻抗作为所有其他阻抗的基础来修改每个组件并指定每个微带的尺寸,那么射频(RF)设计的过程将非常笨拙。
此外,这还假定该项目已经进入PCB阶段。 如果我们想使用离散模块以现成的电缆作为互连来测试和表征系统,该怎么办? 在这种情况下,补偿不匹配的阻抗更加不切实际。
解决方案很简单:选择可在众多RF(射频)系统中使用的标准化阻抗,并确保相应设计组件和电缆,等都已经选择了该阻抗:业界选择的这种标准阻抗的单位是欧姆,数字是50。
50Ω电阻
首先要了解的是,对于50Ω阻抗,本质上没有什么特别的。 虽然您可能会觉得,如果您花了足够的时间来和RF(射频)工程师一起工作,就会感觉到那并不是一个基本的常数。 它甚至不是电气工程的基本常数,例如,请记住,简单地改变同轴电缆的物理尺寸都会改变它的特性阻抗。
尽管如此,50Ω阻抗还是非常重要的,因为大多数RF(射频)系统都围绕该阻抗进行设计。 很难确切地确定为什么50Ω成为标准的RF(射频)阻抗,但是可以合理地假设发现50Ω在早期同轴电缆的情况下是一个很好的折衷方案。
当然,重要的问题不是这个特定值的来源,而是具有此标准化阻抗的好处。 实现完美匹配的设计要简单得多,因为IC,固定衰减器,天线等制造商可以考虑这一阻抗来构建其部件。 而且,PCB布局变得更加简单,因为如此多的工程师都有相同的目标,即设计特征阻抗为50的微带和带状线。
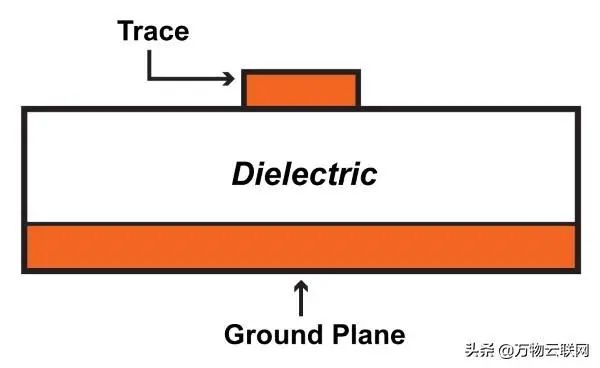
PCB板材的阻抗分布
根据Analog Devices的该应用笔记(MT-094.pdf),您可以按以下方式创建50Ω微带:1盎司铜,20 mil宽的走线,走线和接地层之间的间隔为10 mil(假设采用的是FR-4的电介质材料)。
在继续进行之前,我们要弄清楚,并不是每个高频系统或组件都针对50Ω设计的。 可以选择其他值,实际上75Ω阻抗仍然很常见; 同轴电缆的特性阻抗与其外径(D2)与内径(D1)之比的自然对数成正比。
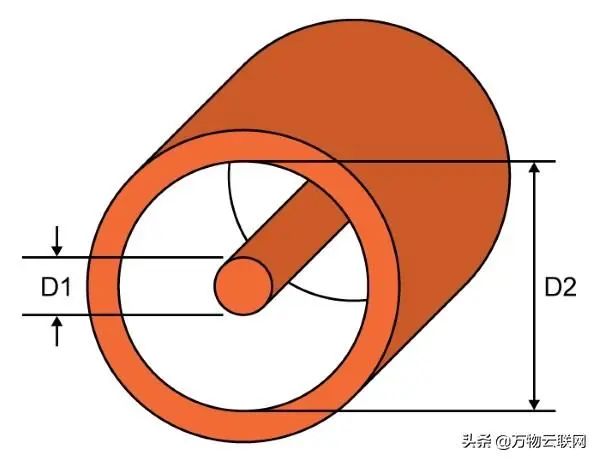
同轴传输线的特性阻抗分布
这意味着内部导体和外部导体之间的更大间隔对应于更高的阻抗。 两个导体之间的较大间距也导致较低的电容。 因此,75Ω同轴电缆的电容比50Ω同轴电缆的电容低,这使75Ω电缆更适合于高频数字信号,因为这种信号需要低电容,以避免与逻辑低和逻辑高之间的快速过渡相关的高频内容过度衰减。
反射系数
考虑到阻抗匹配在RF设计中的重要性,我们不奇怪发现有一个用于表示匹配质量的特定参数。 称为反射系数; 该符号为Γ(希腊大写字母gamma)。 它是反射波的复振幅与入射波的复振幅之比。 但是,入射波和反射波之间的关系由源阻抗(ZS)和负载阻抗(ZL)确定,因此可以根据这些阻抗定义反射系数为:
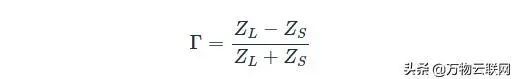
如果在这种情况下“源”是传输线,我们可以将ZS更改为Z0,得到的反射系数如下:
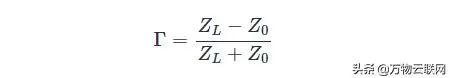
在典型的系统中,反射系数的大小为0到1之间的某个数字。 让我们看一下数学上最简单的三种情况,以帮助我们了解反射系数与实际电路行为的对应关系:
a、如果匹配完美(ZL = Z0),则分子为零,因此反射系数为零。 这是有道理的,因为完美匹配不会导致反射。
b、如果负载阻抗是无限的(即开路,ZL = 无穷大),则反射系数变为无穷大除以无穷大,即为1,而反射系数为1对应于全反射,即所有波能都被反射。 这也是有道理的,因为连接到开路的传输线对应于一个完全的不连续性(请参见上一讲的内容)-负载不能吸收任何能量,因此必将被全部反射。
c、如果负载阻抗为零(即短路,ZL = 0),则反射系数的大小变为Z0除以Z0。 这样我们又有了|Γ| = 1,这也是有道理的,因为短路也对应于不能吸收任何入射波能量的阻抗完全不连续性。
驻波比(VSWR)
用于描述阻抗匹配的另一个参数是电压驻波比(VSWR),定义如下:
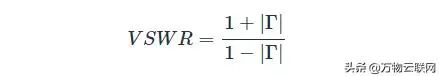
从所得驻波(VSWR)的角度来看,VSWR接近阻抗匹配。 它传达了最高驻波幅度与最低驻波幅度之比。 有很多驻波(VSWR)视频可以帮助您可视化阻抗失配与驻波幅度特性之间的关系,下图显示了三种不同反射系数的驻波幅度特性。
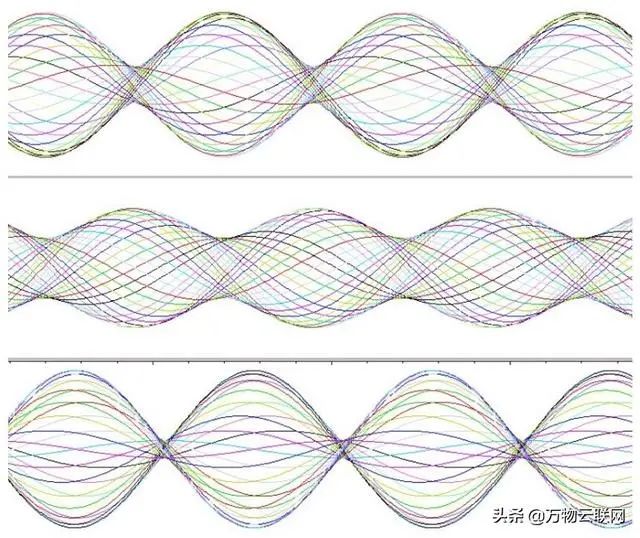
三种VSWR情况下的波形图:更大的阻抗失配会导致沿驻波的最高振幅位置和最低振幅位置之间的差异更大
VSWR通常表示为比率:完美匹配将是1:1,这意味着信号的峰值幅度始终相同(即没有驻波)。 2:1的比率表示反射已导致驻波,其最大振幅是其最小振幅的两倍。
总结
1、标准化阻抗的使用使RF设计更加实用和高效。
2、大多数RF系统的阻抗约为50Ω。 某些系统使用75Ω。 后一个值更适合于高速数字信号。
3、阻抗匹配的质量可以通过反射系数(Γ)在数学上表示。 完全匹配对应于Γ= 0,而完全不连续(其中所有能量都被反射)对应于Γ= 1。
4、量化阻抗匹配质量的另一种方法是电压驻波比(VSWR)。
审核编辑:汤梓红
-
射频设计中的阻抗匹配问题2022-09-29 3255
-
不良阻抗匹配的后果2018-01-19 3343
-
电路阻抗匹配设计2010-08-12 1219
-
基于Ansoft Designer的射频功放电路阻抗匹配优化2009-05-14 3163
-
怎样理解阻抗匹配_pcb阻抗匹配如何计算2018-05-02 44992
-
阻抗匹配是什么意思_阻抗匹配原理详解2018-05-03 53246
-
阻抗匹配电路的作用,阻抗匹配的理想模型2018-08-29 17882
-
50ohm特征阻抗与阻抗匹配等详细资料说明2019-07-30 3343
-
50MHz分立LC阻抗匹配2021-06-04 1357
-
阻抗匹配的原理及应用2022-08-22 4635
-
窄带阻抗匹配电路设计2023-05-15 1618
-
什么是阻抗匹配?高速PCB设计为什么要控制阻抗匹配?2023-10-30 3847
-
RF射频电路为什么选取50欧姆作为阻抗匹配的数值呢?2023-12-07 4090
-
为什么要阻抗匹配?怎么进行阻抗匹配?2024-01-02 4271
-
电路的阻抗如何匹配2024-06-28 4612
全部0条评论

快来发表一下你的评论吧 !

