一文了解如何应用QUBO模型来建模

Ising模型与QUBO模型    

1.伊辛模型(Ising Model)

相干伊辛机(Coherent Ising Machine, 简称CIM), 是目前玻色量子重点研发的一项光量子计算机技术，CIM是一种基于简并光学参量振荡器(DOPO)的光量子计算机，在数学实践中, 我们可以将其抽象为优化Ising模型的专用计算机。

Ising模型是一类描述物质相变的随机过程模型。抽象为数学形式为：

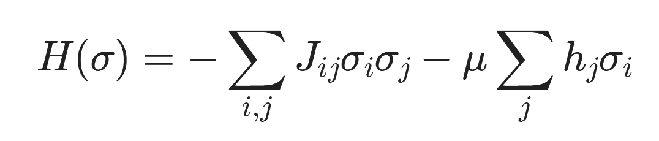
其中σ为待求自旋变量, 取值为{+1，-1}，H为哈密顿量，J和μ分别为二次项系数、线性项系数, 是已知量。

2.区分

QUBO模型更便于建模，Ising模型可以用于CIM求解器直接求解。同时，QUBO模型和Ising模型之间可以互相转化。

1）变量代换

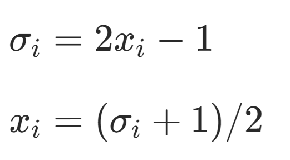
2）创建辅助变量完成一次项转化

QUBO模型建模秘籍    

一、什么是组合优化问题？

组合优化(Combinatorial Optimization, CO)领域是优化领域中最重要的领域之一，它也是运筹学、计算机科学和分析学研究团体所追求的最活跃的研究领域之一。

组合优化是在一个有限的对象集中找出最优对象的一类问题。组合优化的问题特征是可行解的集是离散或者可以简化到离散的，目标是找到最优解。常见的例子有数字划分问题、旅行商问题等。

一般来说，这些问题涉及在必须做出大量是/否决策的情况下做出明智的选择，并且每一组决策都会产生相应的目标函数值，例如成本或利润值。然而在这些环境中找到好的解决方案是极其困难的。

而QUBO建模方式可以包含在工业、科学和政府中发现的各种重要CO问题，借助QUBO求解器的求解能力可以有效地帮助解决许多重要问题。

二、什么是QUBO模型？

QUBO（Quadratic Unconstrained Binary Optimizatoin），无约束二次二进制优化模型是现在量子计算中应用最广泛的优化模型，它统一了丰富多样的组合优化问题。

随着问题规模的增加，利用传统方法求解该问题，求解时间会变得不可接受，但利用QUBO模型可以通过量子计算机加速，高效求解组合优化问题。同时，QUBO模型可以表达位运算，进而表达各种逻辑，操作简便，具体形式如下。

1.基础QUBO形式：minimize/maximize

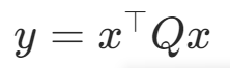
Q为QUBO矩阵，x为二进制变量组成的向量，每个变量取值均为{0,1}，QUBO目标为找到使得y最小或最大的x

其中，Q矩阵的形式有2种：

1）对称形式

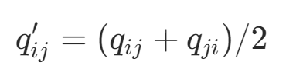
2）上三角形式

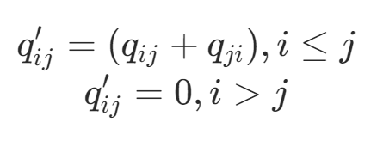
举例：

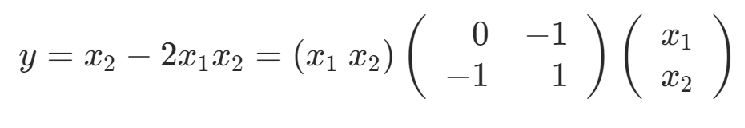
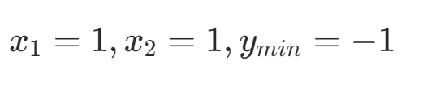
2.位运算

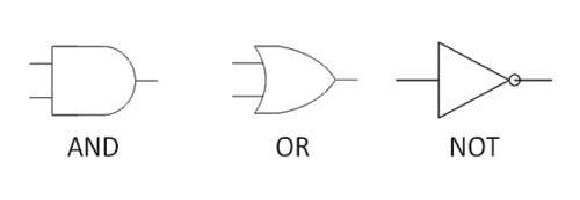
与 同时为1，结果才为1；

或 同时为0，结果才为0；

非 0变成1，1变成0；

异或 两位相同为0，相异为1

位运算表达

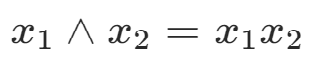
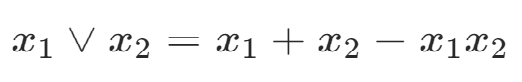
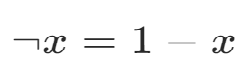
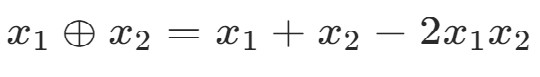
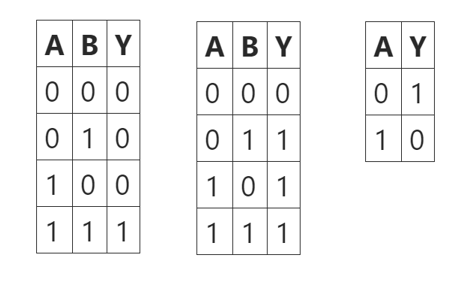
3.添加约束条件

举例1：

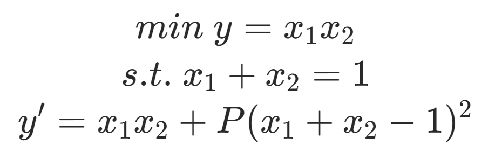
通过添加约束项，并设置较大的系数P保证约束内容的优先级。

举例2：

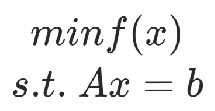
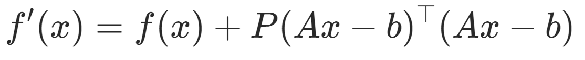
约束条件举例

     

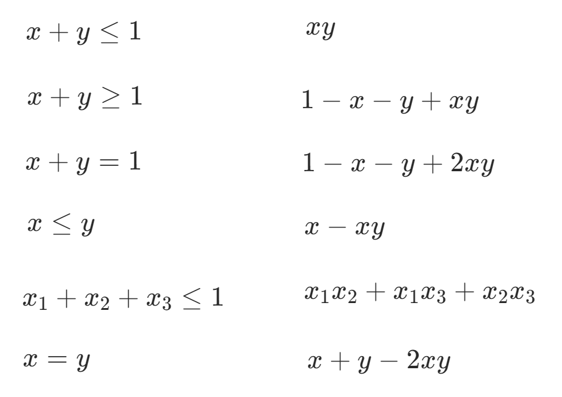
4.整数表达

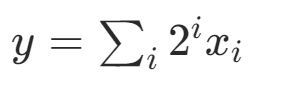
通过二进制表达整数，使用d个变量可以表达0到2^d −1 的数字。

举例：

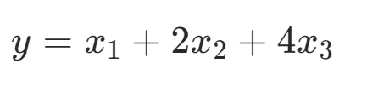
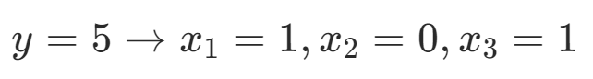
5.不等式约束

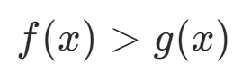
不等式约束可以转化为等式约束，通过松弛变量y表示出不等式两边的差。

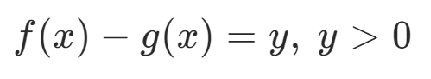
其中y为通过二进制表达的整数，构造约束项：

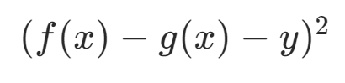
（注意点：这样做会引入新的变量，增加问题规模）

6.扩展思考

HOBO问题（High Order Binary Optimization），是指用二次多项式难以表达的高次问题。对于高次的问题，可以将x1x2替换为y，并添加约束项使得x1x2=y，从而将高次的问题转化为二次优化问题。

约束项：Rosenberg多项式

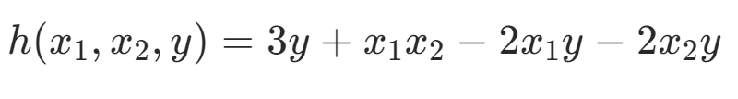
满足：

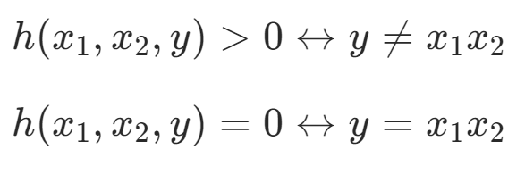
（注意点：这样做会引入新的变量，增加问题规模）

三、QUBO可以解决哪些问题？

最大独立集问题

不对称分配问题

对称分配问题

边约束分配问题

二次背包问题

最大团问题

最大割问题

整数划分问题

旅行商问题

举例1：整数划分问题

1）整数划分问题（The Number Partitioning Problem），NP-complete将包含n个非负整数的数集划分为两个子集，使这两个子集的和尽可能接近

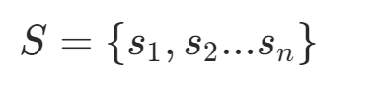
设数集为

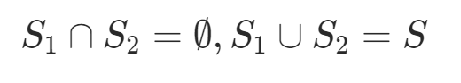
选两个子集满足，使得下值最小

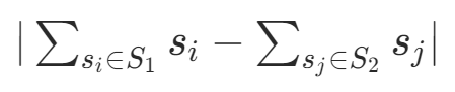
举例S= {1，2，3，4，8}，一组最有解为S1= {1,8} S2={2,3,4}是一组最优解，两者的和均为9

2）整数划分问题建模思路

1. 定义决策变量，决定每个整数被分到哪一个集合

2. 使用决策变量表达出两个集合整数和的差值

3. 通过CIM优化目标函数，得到最小值对应的解

3）整数划分问题建模过程

定义决策变量xi，xi=1表示 Si∈S1，xi=0表示Si∈S2

两个子集求和的差值：

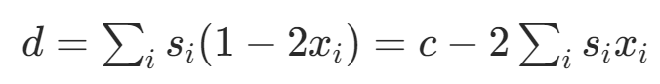
目标函数：

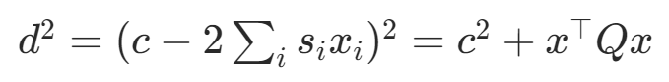
其中，

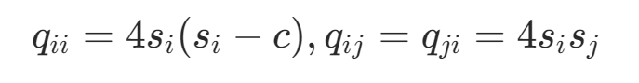
举例2：旅行商问题

1）旅行商问题（Traveling Salesman Problem）NP-Complete，商人想要在地图上走完所有城市，每个城市只经过一次，最后回到最初的城市，求路程最短的走法。

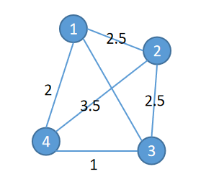
给定带权图G(V,E)，V为点集，E为边集，要求遍历所有点再回到初始点，求路程最短的走法。哈密顿回路：遍历所有点再回到初始点。

举例：

2）旅行商问题建模思路1.0

以下图为例，定义决策变量xi,u，表示“经过的第i个节点为u”是否为真，通过决策变量表达出距离，再通过添加约束条件使得求解方案能够成立，构造得到表达式通过CIM进行优化。

目标包括：

1. 路程最小

2. 路线为环（约束自然满足）

3. 同时只能经过一个节点（约束）

4. 每个点经过次数为1（约束）

5. 不能走不存在的连接（约束）

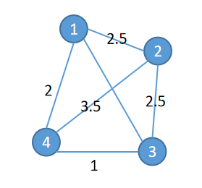
3）旅行商问题建模过程

设有n个节点，wu,v从u到v的边的边权，定义决策变量xi,u，表示“经过的第i个节点为u”是否为真，路程为环可以根据决策变量的定义自然满足，则经过的路程可以表达为：

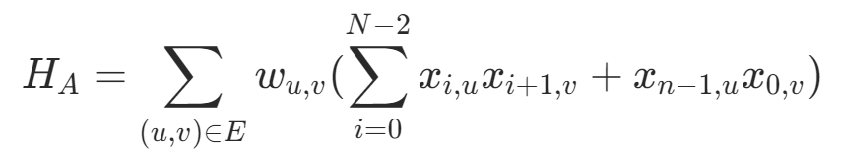
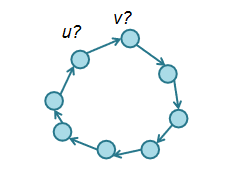
4）旅行商问题约束条件

为使得xi,u符合实际情况，需要如下约束：

第i个节点只有一个节点

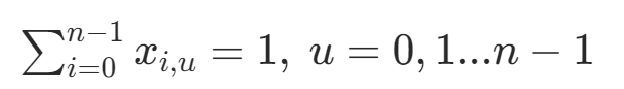
节点u只在路线中出现一次

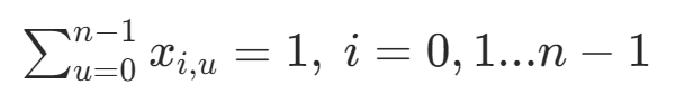
可以根据以上两个条件构造约束

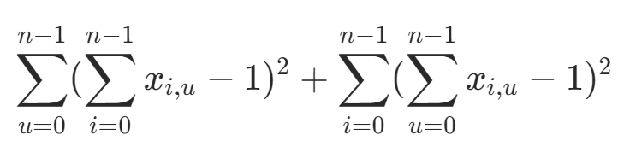
为了保证不存在的边不出现在方案中设置约束项

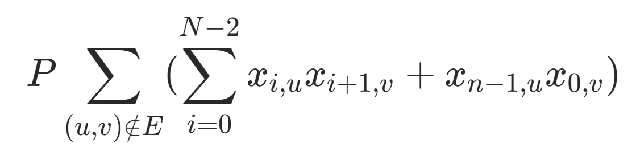
P为惩罚项系数，取值需要显著大于其他边权，最终的约束项：

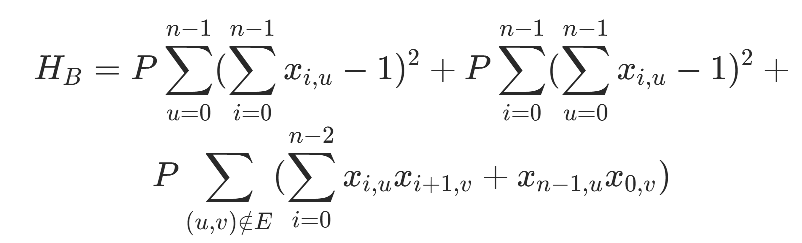
目标函数包括回路总长和约束两部分：

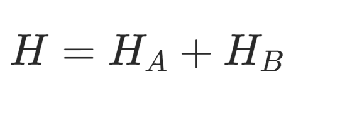
2）旅行商问题建模思路2.0

定义决策变量xu,v，表示“使用u到v的边”，通过决策变量表达出距离，再通过添加约束条件使得求解方案能够成立，构造得到表达式通过CIM进行优化。

目标包括：

1. 路程最小

2. 每个点出发一次（约束）

3. 到达每个点一次（约束）

4. 不能走不存在的连接（约束）

由于相干光量子计算最擅长攻克组合优化问题，可应用赋能场景广泛，如金融业的投资组合优化、资本风险分析建模；生物制药业的蛋白质折叠、小分子组合和DNA重组；

交通物流行业路径优化等，这些都是在实际工作中经常遇见的复杂度很高且计算量巨大的常规问题，所以该技术路线高度贴合市场需求，普适率高。

 




审核编辑：刘清