车载毫米波雷达的DOA估计方法框架设计方案

本篇博文我是想尽可能囊括足够多的DOA估计方法。DOA算法其理论的理解和公式的推导需要较强的数学功底以及信号处理相关知识的积累，博主本人是转专业来的，是该方向的后闻道者，且入行没多久，相关的理论知识积累少也不扎实，涉及到的公式非必要我会尽量少放。 本篇博文不会讨论这些DOA估计算法的具体原理/公式推导(相关的资料在网上有很多)，而是侧重于试图搭建一个常见的适用于(或可能适用于)车载毫米波雷达的DOA估计方法的框架。  

车载毫米波雷达DOA估计方法概述

目标角度估计，特别是角度分辨率的提高是雷达探测需要解决的核心问题，传统的车载毫米波雷达其实对角分辨率的要求并不高，几度甚至十几度的角分辨率是很多商用角雷达与前向雷达的测角指标，且这些雷达并不具备俯仰向测角能力。但是随着辅助驾驶乃至无人驾驶对传感器的要求越来越高，二维测角能力以及更高的角分辨率(甚至低于1°)成为了车载毫米波雷达的标配。比如近几年发展起来并开始逐步商用的4D毫米波雷达。 使用FFT与DBF做DOA估计是最简单且运算复杂度最低的方法，但是这两方法并不能实现超分辨，其角分辨率受限于阵列的孔径，比如对于均匀排布的阵列，角分辨率有公式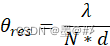： 式中，N为阵元个数，d为均匀阵的相邻阵元间距，该式得到的是雷达法向的角度分辨率。从上式可以看出，如果要提高角分辨率那只能通过增加天线数量来增加阵列孔径，但是天线数量和孔径不能不受限地增加，否则包括硬件成本、数据量、尺寸等都没法满足实用要求。 于是催生了所谓的压缩感知：期望使用较少数量的阵元通过稀疏布阵的方法以达到较高的测角分辨率，关于压缩感知，又有多种针对稀疏阵列的测角方法: 1、还是直接对稀疏阵元使用DBF测角，此时相较于均匀阵列，必然有很多空缺的阵元，这些空缺的阵元会导致很多很高的旁瓣出现，如下图所示：

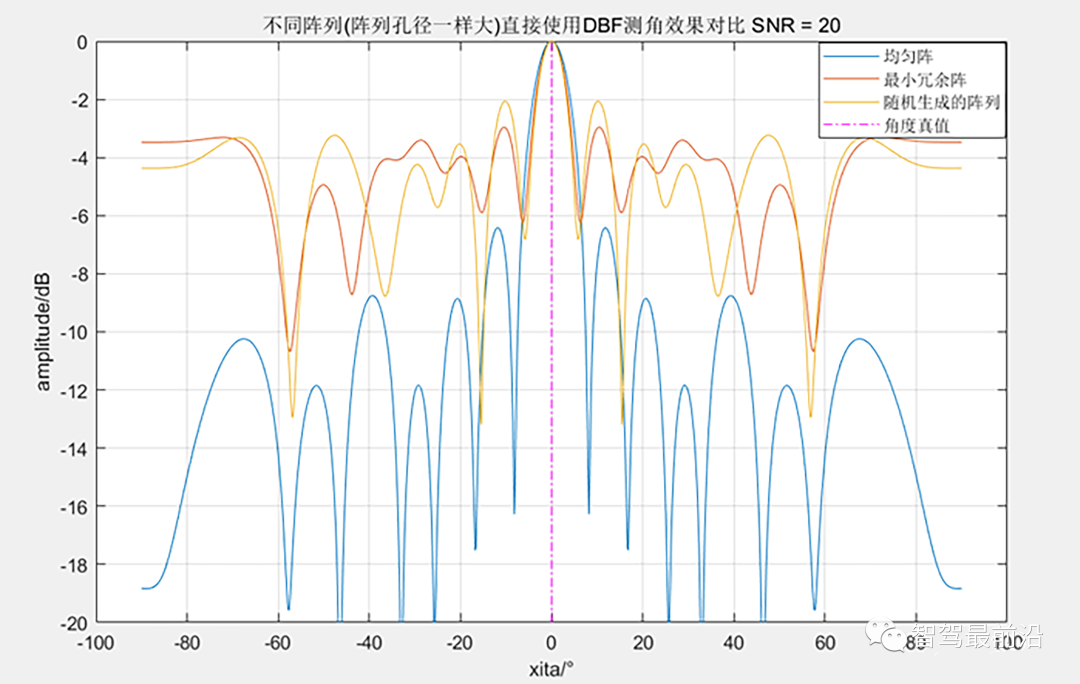
同阵列孔径下，均匀阵与稀疏阵的阵列方向图对比 仿真中，均匀阵的大小为[013],最小冗余阵对应[0 1 2 6 10 13]，生成的随机阵列为[0 1 2 5 11 13]，从图中可以看到，当阵列中有空缺的阵元时，直接使用DBF或许也能看到目标的位置，但是旁瓣极高。当目标不止一个或者SNR值很低，此时稀疏度较高的阵列直接使用DBF测角是不适用的，如下所示：

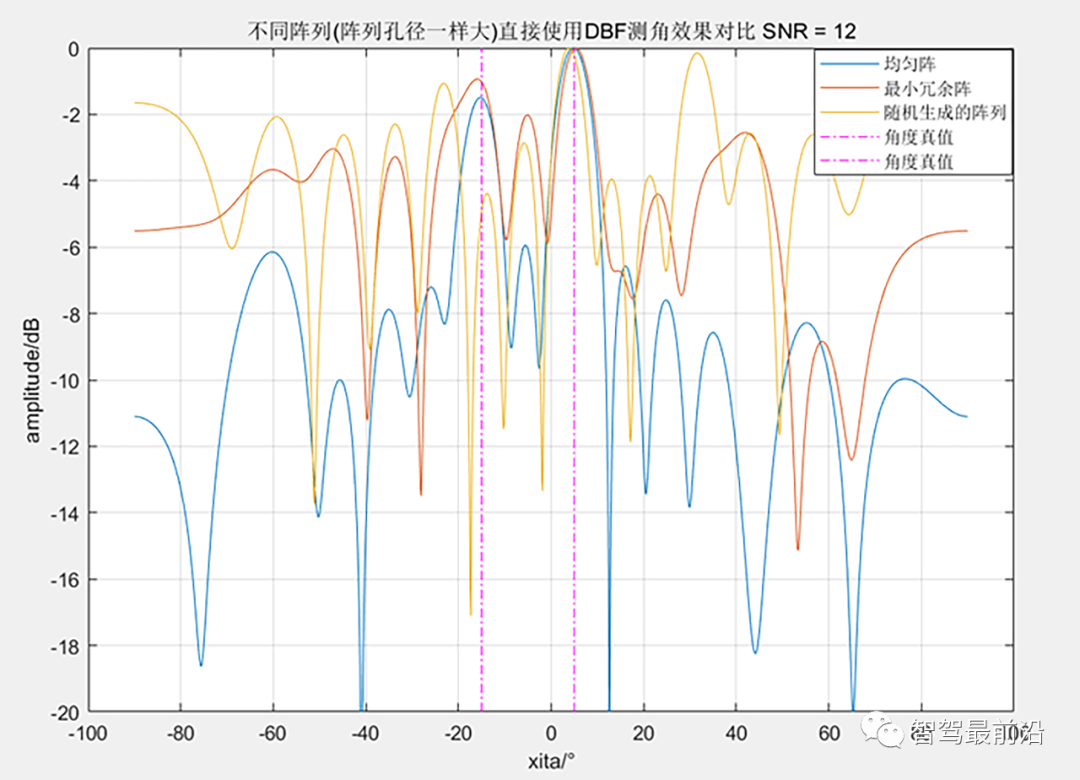
从图中可以看到，只有均匀阵的还能准确地分辨出两个目标 2、阵元补全：将空缺的阵元位置的信息通过一些方法(在后文做介绍)进行补全，随后再使用DBF等方法基于补全后(等效为均匀阵了)的阵列信息做角度估计。这种方法可以达到近似均匀阵的效果，但是运算量会上来，且补全算法的可实用性可能对依赖于特殊的阵列。

3、基于凸优化或者贪婪近似方法做超分辨的角度估计，比如正交匹配追踪算法OMP以及迭代自适应算法IAA等，这两种方法允许阵元不全（自然它们也可以用于均匀阵！），且其相较于其它超分辨算法，它们不需要多快拍数据、也不需要提前知道信号源的个数，但是计算量大。 除此之外，则是一些超分辨算法了，常见(但是不常用于车载毫米波雷达)的包括：最大似然估计(DML，DML作为一种需要多快拍也需要提前知道信源个数的超分辨率测角算法很意外地在实际产品中被广泛使用，特别是基于加特兰的芯片开发的雷达产品，加特兰在其芯片中将该算法硬化了)、Capon、MUSIC、ESPRIT等超分辨测角算法，但是这些超分辨算法其测角结果的准确性大多依赖于多快拍的回波数据以及信号的高SNR。

如前所述，现阶段对车载毫米波雷达的要求已经不限于一维测角了，当需要做二维的角度估计时，就又产生了诸多的2D-DOA估计方法，2D-DOA估计最简单是对面阵做2D-FFT或2D-DBF，随后在得到的矩阵中找极大值，并根据该极大值所在的索引值得到目标的二维角度。在该方法的基础上，一种容易想到的改进方法是：首先对测角面阵只做水平向或竖直向的FFT或DBF，随后找到其极值点，并得到水平向或竖直向的角度值，再对这些极值点所在的另一维度做FFT或DBF,得到竖直向的角度以完成2D-DOA估计，基于面阵直接进行二维压缩的方法不需要进行角度匹配，算法简单，但是对阵元数的要求高。另外的一些方法则是分别在水平和竖直向做独立的角度估计，再基于一些匹配方法做目标水平和竖直向的角度匹配以完成目标的2D-DOA估计，这类方法并不需要是面阵，减少了天线数量但是算法复杂度上升。我会在后文中简单介绍两种匹配方法。 总结来说，后文将涉及：FFT、DBF、IAA、OMP、DML、Capon、MUSIC、ESPRIT等测角算法、稀疏阵列补全方法、目标2D-DOA估计方法，并简要讨论超分辨算法在车载毫米波雷达中实用的可行性。在此重申，相关的内容比较少涉及具体的公式推导(但是我会尽可能多地提供相关的测角效果对比，相关的仿真代码等阅读量到一定程度后再公开)，内容会随着积累不定期丰富。 补充说明： 前文提及到了4D毫米波雷达，4D毫米波雷达性能评价的最核心指标便是角度分辨率，这里对现阶段商用4D毫米波雷达的几种实现路线做一个简单介绍，现阶段商用4D毫米波雷达产品主流的实现方式主要有4种：

1、级联的方案：通过多芯片级联来增加通道数，主流的Tier1比如大陆、博世、安波福，以及华为的4D毫米波雷达都是用的多芯片级联方案。

2、“单芯片”方案：这种方案的出发点和级联方案是一样的，只不过是做出了更厉害的芯片，在单颗芯片上便实现传统芯片多芯片级联才能达到的通道数，比如Arbe的48T48R产品仅仅使用了2颗发射芯片和4颗接收芯片，且其数据处理部分也有专用芯片。

3、软件手段：对实际通道数的要求低，只需要很少量的通道数，该技术路线通过算法和软件的方法构建虚拟通道使分辨率成量级地提高。比如傲酷。 4、超材料方案：MetaWave的超材料成像雷达，大概是基于材料的特殊特性，通过波束扫描(相控阵)来实现极高的角分辨率。  

几种常见的DOA估计方法及其对比总结

阵列的DOA估计需要明白的一点是：测角算法应该是需要与具体的阵列相结合的。合格的毫米波雷达产品应该是合适的阵列设计再加上对应的合适的信号处理(测角)算法。

2.1 FFT与DBF

这两是最简单的测角算法，且效果几乎一致。最早的基于阵列的DOA算法便是常规波束形成算法（CBF或DBF），DBF本质是构造视场范围内的各个角度的导向矢量，并用这些导向矢量分别去和阵列的回波信号相乘以得到各个角度下的能量值，我们通过寻找其中的极大值(目标所处方向的回波与导向矢量相干叠加，这些方向的能量会得到增强，而噪声是非相干的，能量得到增强的方向，对应极大值的位置，也即信号的方向)来得到实际回波的方向而达到测角的目的。与时域相比，测角是以空域各阵元接收的数据替代传统时域处理中的时域数据，所以与时域的傅里叶限制一样(FFT后的频率分辨率取决于采样时间: df = 1/T)，将这种方法扩展至空域后，阵列的角分辨率同样受到空域傅里叶限(此时是阵列的孔径：θres=λ/(N*d)的限制。如果要提高测角分辨率就只能通过增加孔径来实现。以下给出不同阵列孔径下的DBF与FFT的测角效果：

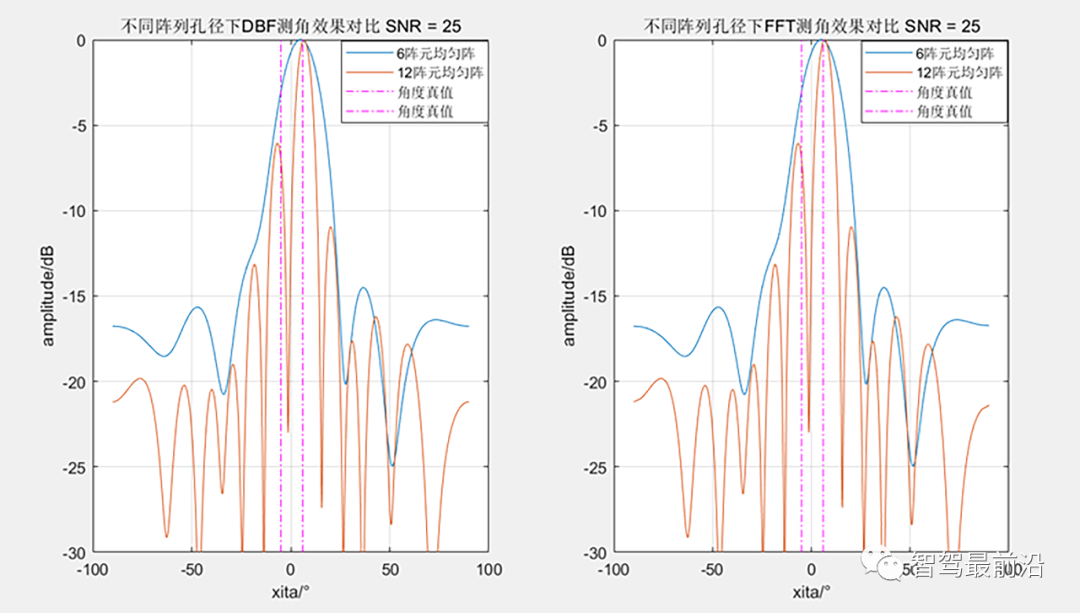
不同阵列孔径下的测角效果对比 FFT与DBF的测角效果一致。为方便比较，后续各种测角算法下的测角效果都会将之与DBF下的测角效果做对比。

2.2 Capon(或称MVDR，最小方差无畸变算法)

波束形成的算法有很多(可以参考之前提到的书：《阵列信号处理及MATLAB实现》，Capon是其中较为经典的一种，除此之外还有比如：MMSE、MSNR等)，前述DBF严格来说应该称为CBF（常规波束形成），是最简单的一种波束形成算法，这么多波束形成算法其主要区别在于前面提及的导向矢量(或权矢量)的不同，比如前述CBF的导向矢量为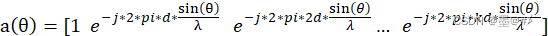： 式中，d为阵列阵元之间的间距，k为阵元个数，θ在测角范围内变化，我们用上述向量去和回波信号相乘，得到不同角度下的能量结果。而对于Capon算法，其权矢量变成了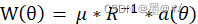： 式中，a(θ)同前式，R为信号的协方差矩阵，θ在测角范围内变化，μ为常数，对应特定方向下经过该Capon算法后的能量值，结合约束条件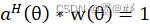： 可以得到不同角度下的能量值的估计式为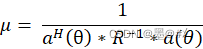： 在该式的指导下，我们求解并得到不同角度下的能量值，找到极大值点的位置即可得到目标的角度。注意到信号协方差矩阵R的准确估计依赖于多快拍的回波数据以及高的SNR，所以该算法需要多快拍数据做支撑。不同快拍数下的效果对比如下：

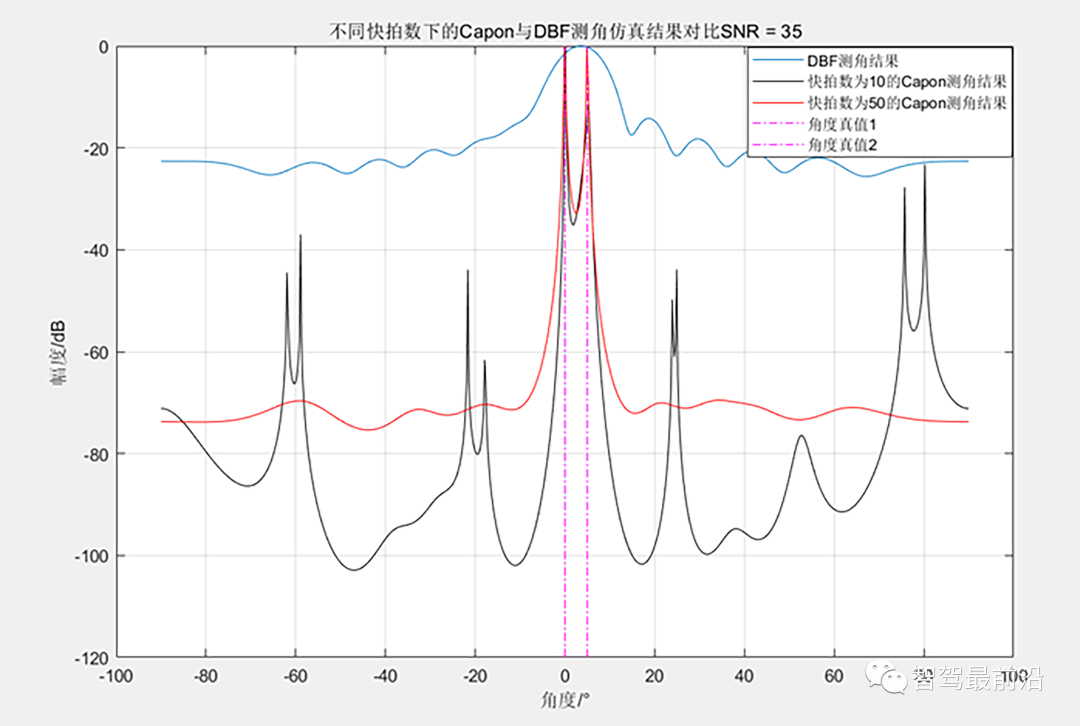
12阵元均匀阵下的Capon与DBF仿真结果对比 目标处在0°和5°，可以看到DBF下无法做到超分辨，但是Capon算法下看到了两个明显的峰，做到了超分辨测角(该算法可以做到多少倍的超分辨主要与SNR有关)，仿真结果中还给出了不同快拍数下的Capon算法对比，可以看到多快拍数下的测角结果明显优于低快拍数(这是一个比较定性的说法，至于在特定的SNR下多少快拍数可以满足测角要求，不在本博文的讨论范围之内)。

2.3 MUSIC & ESPRIT

这两都是基于协方差矩阵的特征分解类DOA估计算法，都是非常优良且经典的超分辨DOA估计方法。MUSIC相对容易理解一点，利用的是噪声特征向量与信号向量的正交关系，ESPRIT是基于信号子空间的旋转不变性？具体的原理我理解一二但是很难简单说清楚，读者可以参考前面提到的书本。 这两种方法相较于前面的Capon算法除需要较多的快拍数和高的SNR以得到精确的协方差矩阵估计外，还需要知道信源个数，这是限制其应用于车载毫米波雷达的另一个重要原因。【不过对于非4D雷达，我们在做角度测量时可以限制其一个距离和速度门下只有一两个目标？后文将提及的DML算法也需要知道信源个数，限定信源个数是加特兰芯片中应用DML算法的一个基本前提。】具体到这两种超分辨算法，MUSIC对信源个数的要求似乎不那么严格一些，比如实际目标有3个，使用MUSIC算法是给定目标个数大于等于3时，其测角的波峰结果仍会是3个，而如果给定目标个数小于实际目标个数，则测角的波峰结果会等于给定的目标个数。而ESPRIT的输出结果等于给定的目标个数，不管实际的目标个数是多少。

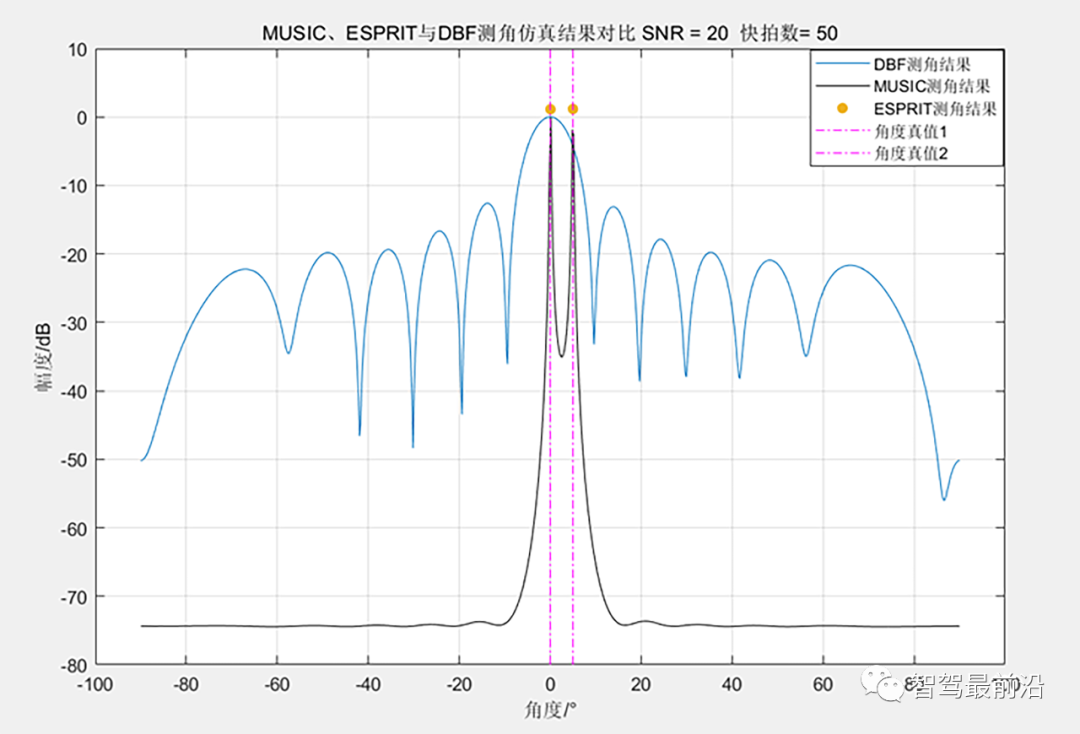
12阵元均匀阵下MUSIC、ESPRIT与DBF测角结果对比 目标在0°和5°位置，MUSIC和ESPRIT都准确地估计到了目标，具备超分辨能力，但是DBF下两目标隐藏在了一个波峰里面。同Capon中的说明，SNR越高和快拍数越多，其超分辨的能力越高，不过固定的快拍数下，这两算法对SNR的要求相比Capon似乎要低一些，此外其实这两算法对快拍数的要求也不是太高(但是单快拍是不行的)，几个快拍加上比较好的SNR超分辨的效果就很好了。

2.4 DML(最大似然法)

在《阵列信号处理及Matlab实现》这本书中，对DML的介绍是：在信号处理中，最著名和最常用的建模方法是最大似然法。基于最大似然的波达方向估计方法分确定性最大似然法(Deterministic ML，DML)和随机性最大似然法(Stochastic ML，SML)两大类型，我们这里讨论和使用DML。 具体的原理可以参考书本，我后面所做仿真是基于加特兰baseband中对其DML算法的介绍而写的代码，原理比较简单，我直接贴那段话的图吧：

加特兰Baseband使用手册中对DML算法的介绍 其中A(θ)为导向矢量矩阵，X为接收信号，R为信号的协方差矩阵，本算法是要求出使得P*R这个矩阵的迹最大时对应的角度(或如果有多个目标的话，则是角度集合)，算法是要做遍历的，且在特定的角度扫描个数(比如从-75°到75°设定角度扫描个数为N)下其算法复杂度和信源个数D的关系为：Ο(ND)。DML算法也是需要多快拍的数据以及知道信源个数的，上面提到过加特兰在其芯片中应用该算法的一个基本前提是对一个距离和速度门下的目标个数做了限定(不超过两个)，而且信源个数一多计算时间也会增加，而车载雷达对更新率是有要求的，此外，加特兰在其baseband中说According to the result of simulation, DML performs well in some respects. It can separate incoming signals with small angle differences even in single snapshot case, so in our DML engine, we use only one snapshot to do the angle estimation，用单快拍的数据来获得协方差矩阵在DML中似乎也可以接受。以下为DML和DBF的仿真结果对比：

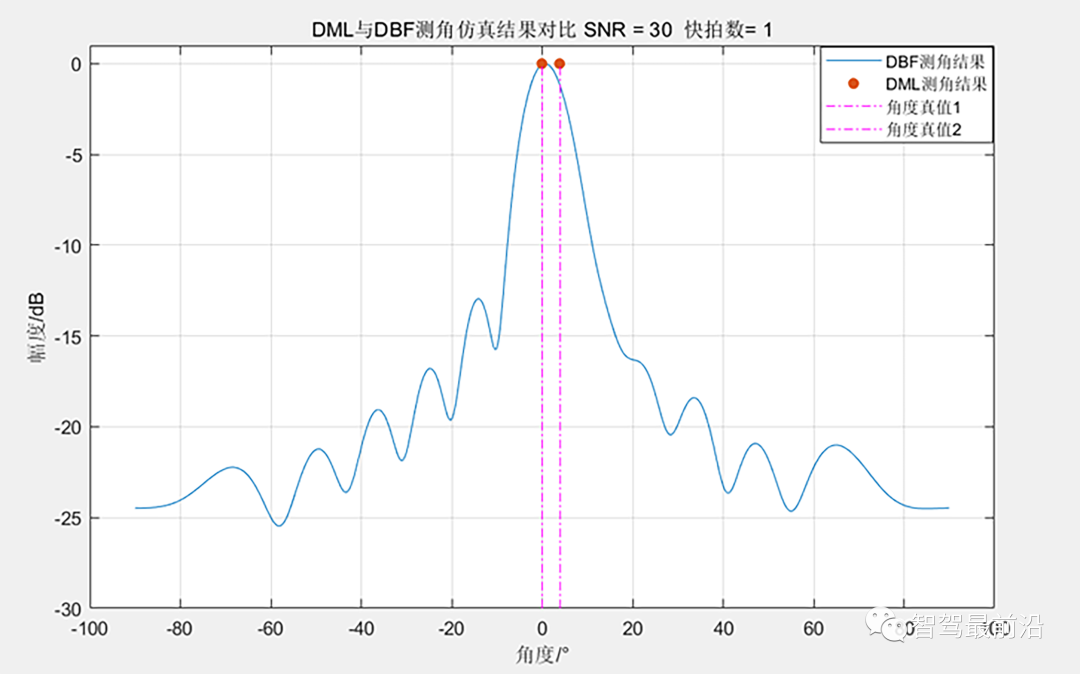
12阵元均匀阵下MUSIC、ESPRIT与DBF测角结果对比 目标在0°和4°的位置，DML算法准确地测量到了目标，且做到了超分辨。DBF下两目标隐藏在了一个波峰里面。此外，仿真结果显示，DML算法对SNR的要求较高。

2.5 OMP(Orthogonal Matching Pursuit 正交匹配追踪算法)

OMP是一种信号重构算法，将该算法用于角度估计的基本原理是：假设有K个目标，入射到M个天线构成的均匀线阵上，设第K个信号的入射角度为θk,则阵列t时刻接收到的信号为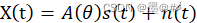： 式中，A为信号的方向矢量矩阵，s为信源矢量，n为噪声。(这个公式比较简单，容易理解，就略过了)，我们将A进行拓展，A之前的大小是K*M，K表示K个目标方向，将之扩展到包含雷达视场范围内的所有可能的方位角(比如[-7575])，此时假设其大小变成了N*M，我们用G表示，此时上式变成：x = G*γ+n，γ为N维的系数向量，且由稀疏理论可知，γ中非零元素个数应该为K(目标个数)，γ中非零元素的位置对应向量的对应角就代表了入射角θ的值，我们可以用OMP算法求解该问题（等价于求解扩展后的方向矢量矩阵中各个角度的贡献值：知道了G和x来求γ，就是上面博客中的问题）。

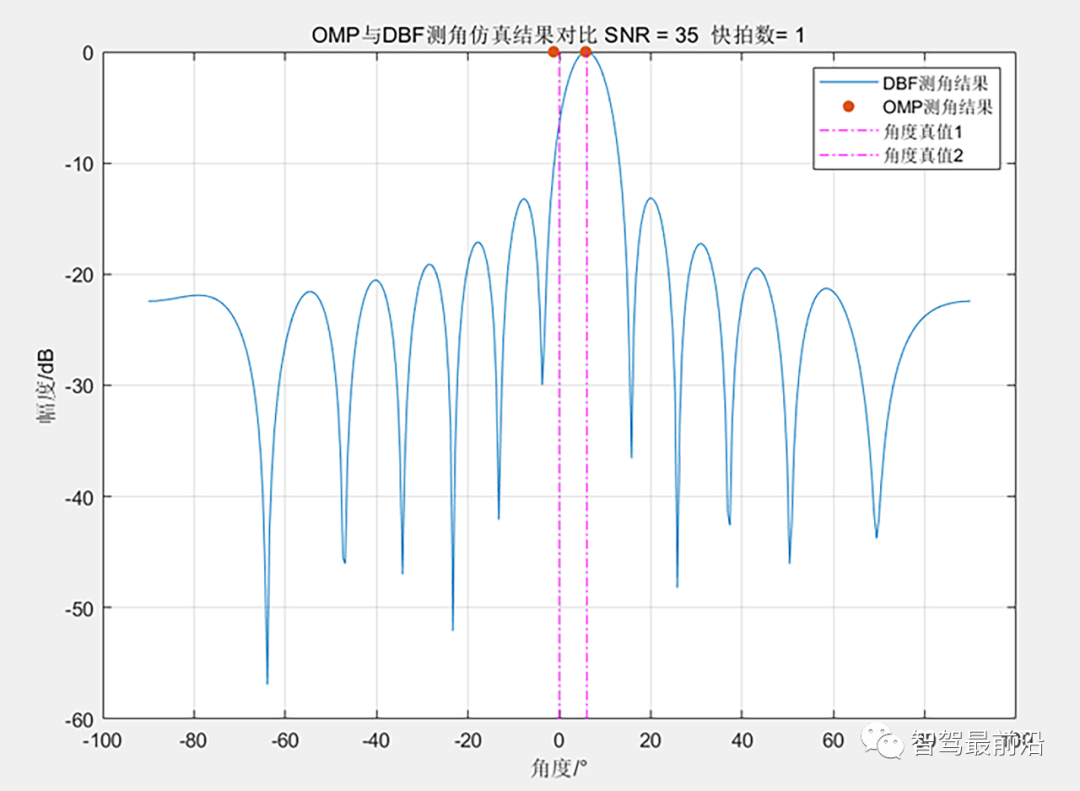
12阵元均匀阵下OMP与DBF测角结果对比 目标在0°和5°的位置，OMP算法差不多准确估计到了目标位置(精度有些问题，大概是写的OMP算法有点不对..), DBF下两目标隐藏在了一个波峰里面。OMP算法只要求单快拍的数据，但是需要知道信号源的个数。

2.6 IAA(Iterative Adaptive Approach,迭代自适应法)

网上对IAA算法的介绍好像很少，IAA是一种基于加权最小二乘法的非参数方法，具体的理论我也讲不清楚，后面找到比较好的介绍资料我再贴出来，这里直接给出仿真结果：

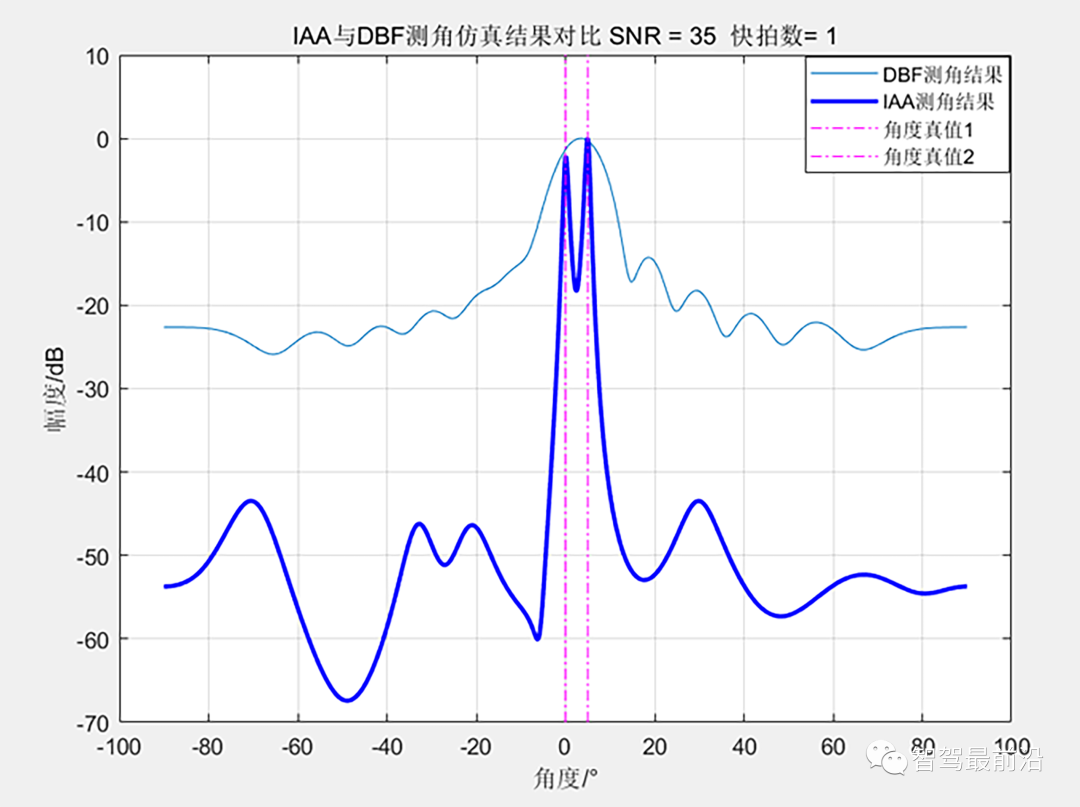
12阵元均匀阵下IAA与DBF测角结果对比 目标在0°和5°的位置，IAA算法准确地测量到了目标，且做到了超分辨。DBF下两目标隐藏在了一个波峰里面。此外，仿真结果显示，IAA算法虽然可以在单快拍下测角，但是如果SNR也很低那么超分辨的效果将很差(超过角度分辨率一点点可能就分辨不出来了)。该方法需要知道信源个数。

2.7 阵元补全

本小节的内容讨论稀疏阵下的空缺阵元补全的方法，所谓的阵元补全就是基于实际的稀疏阵列排布和实际存在的阵元所接收到的信号，采用一定的方法将相较于均匀阵列空缺的位置的回波信息恢复出来(在此过程中也可能会改变原有阵元位置处的原始接收信息)。之后基于恢复后的(不那么稀疏的)阵列进行测角等处理。 这里给出两种方法，并给出阵元补全前后以及同等孔径均匀阵下的DBF测角结果对比。 A、基于协方差矩阵向量化与差分集合 有一篇硕士毕业论文比较清楚地讲解了该方法的原理，但是找不到了(后面如果找到我再贴上来)。该方法首先求解稀疏阵列所接收回波数据的协方差矩阵，随后将该矩阵向量化，按照原稀疏阵列对应的差分集合中元素的顺序和值，选取对应的协方差矩阵向量化后的元素来构造等效的（更均匀）的接收阵列回波数据。该方法需要多快拍的数据，且差分集合中的值重复得越少对应恢复的效果越好，最小冗余阵列其差分集合中的值都是唯一的，所以用该方法恢复最小冗余阵列性价比最高。

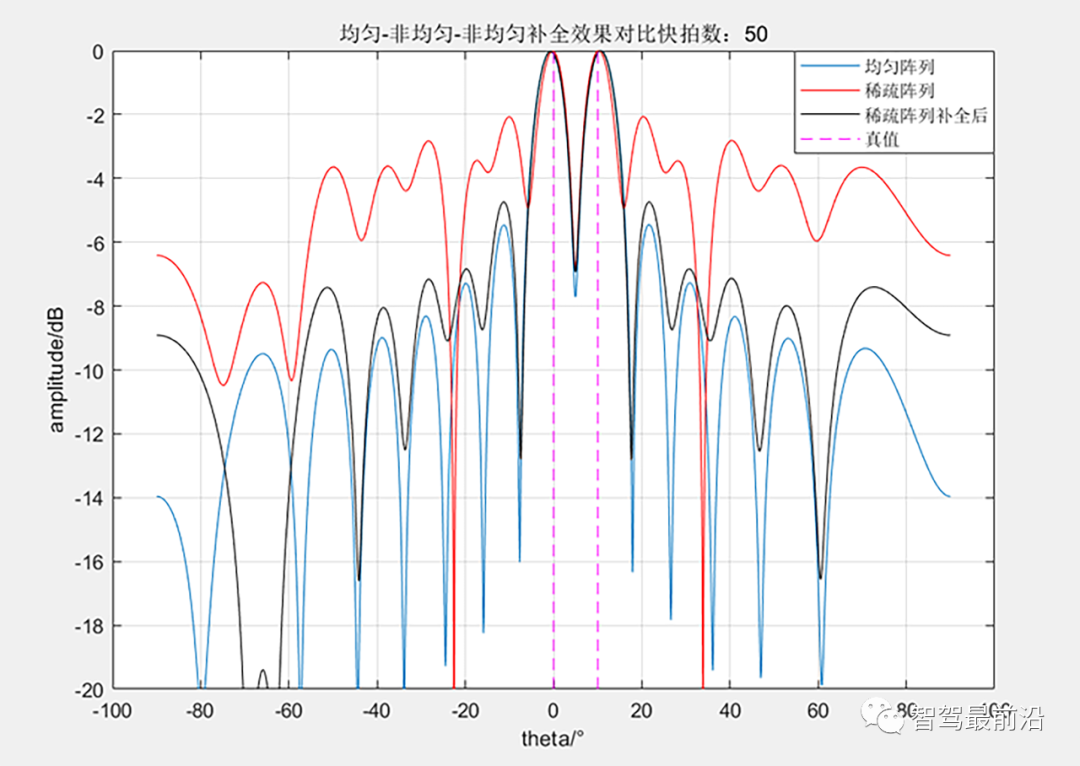
6阵元最小冗余阵[0 1 2 6 10 13]的补全前后仿真效果对比 目标在0°和10°的位置，可以看到，使用该方法进行阵列补全恢复后的测角效果与均匀阵下的测角效果几乎一致，而恢复前因为有大量空缺的元素存在，导致旁瓣拉高(我在前述第一章中有说明)，这也是阵列补全的意义所在。此外从仿真的结果来看，使用该方法对阵列进行恢复随着阵列稀疏度和孔径的增加对SNR和快拍数的要求也会更高，否则效果会较差。 B、基于奇异值阈值算法(Singular Value Thresholding, SVT) 这是一种数学上的矩阵恢复方法?基于稀疏阵列的回波数据信息去构造一个矩阵(该矩阵可以是Hankel矩阵、Toeplitz矩阵或者其它)，随后基于SVT算法和一定的原则来补全这个构造的矩阵，从该补全后的矩阵来得到均匀阵列的信息。矩阵填充理论是一种重要的数据处理方式，假设矩阵满足低秩性，但是矩阵的部分元素缺失导致信息不完整，矩阵填充理论通过利用已知信息，按照矩阵低秩的约束，来将缺失的信息补全。 关于使用Hankel矩阵+SVT算法的详细说明和理解，可以参考Shunqiao Sun的相关论文，我在后文的参考文献中给出了其中的两篇。本小节的仿真也参考了其论文，这里给出基于Hankel和Toeplitz矩阵与SVT算法下的仿真结果对比。

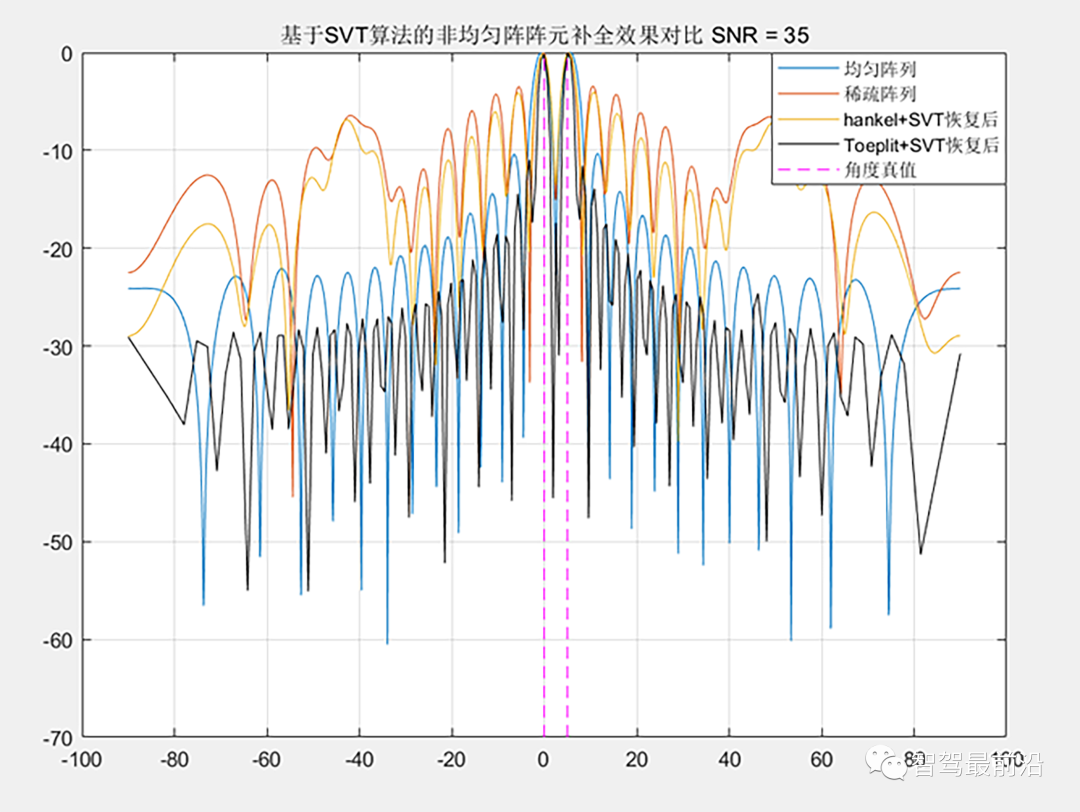
8阵元最小冗余阵[0 1 2 11 15 18 21 23]下补全前后的效果对比 目标在0°和5°的位置，基于Toeplitz方法恢复后的测角效果甚至优于均匀阵列，该方法用到了共轭信号？测角分辨率有一倍的提高？。基于Hankel矩阵的方法看起来效果不是很好，该方法的效果似乎与阵列的排布有很大的关系，且阵列孔径越大该方法下的效果提升似乎会显著一些，如下：

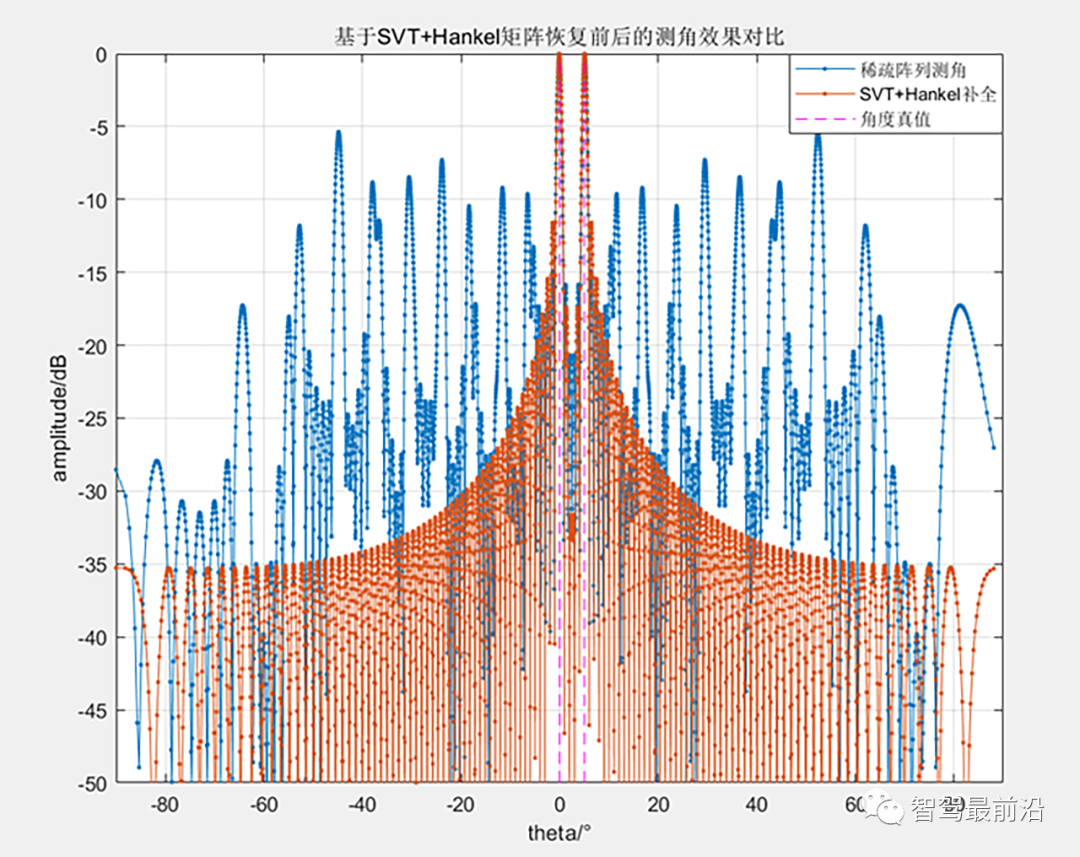
{[1 4 5 6 9 12 14 15 21 24 25 26 29 32 34 35 41 44 45 46 49 52 54 55 61 64 65 66 69 72 74 75 81 84 86 89 92 95 101 104 105 106 109 112 114 115]-1}该阵列下的阵元补全前后的测角效果对比 目标在0°和5°的位置，可以看到测角效果有明显的提升。该阵列为前面提到的Sun的论文中给的阵列。

2.8 一种“空间多快拍”的方法

测角的方法还有很多，但是各有要求以及优劣，能做工程应用的要少很多，能应用于车载的就更少了。本博文上面给出了比较经典和常见的几种方法(或者也可以说是博主现阶段有所积累的方法)的测角仿真效果以及各自的应用要求(对SNR和快拍数)，我会基于后续的学习和工作不定期更新一些较为有用且有意思的新算法。  

2D-DOA估计方法讨论

对于4D雷达，我们需要同时知道目标的水平和竖直向角度值以得到目标位置的准确测量。这便涉及到水平和竖直向角度的联合估计问题。在前文第一章中对该问题做了简单的叙述，本章对该问题进行详述，并给出几种角度匹配的方法。

1、无需进行角度匹配

类比我们对采集的ADC数据矩阵进行距离和速度维度的压缩之后，通过检测矩阵中的极值点(基于CFAR)，这些极值点的二维索引对应的就是该目标的距离和速度值。对于一个已知了距离和速度值的点(我们暂时还不知道满足这个条件下有几个目标)，我们将该点通道维度的数值按照实际的二维阵列排布得到一个数据矩阵，对该数据矩阵进行二维压缩,通过检测矩阵中的极值点，这些极值点的二维索引便对应了该目标的二维角度值。

 

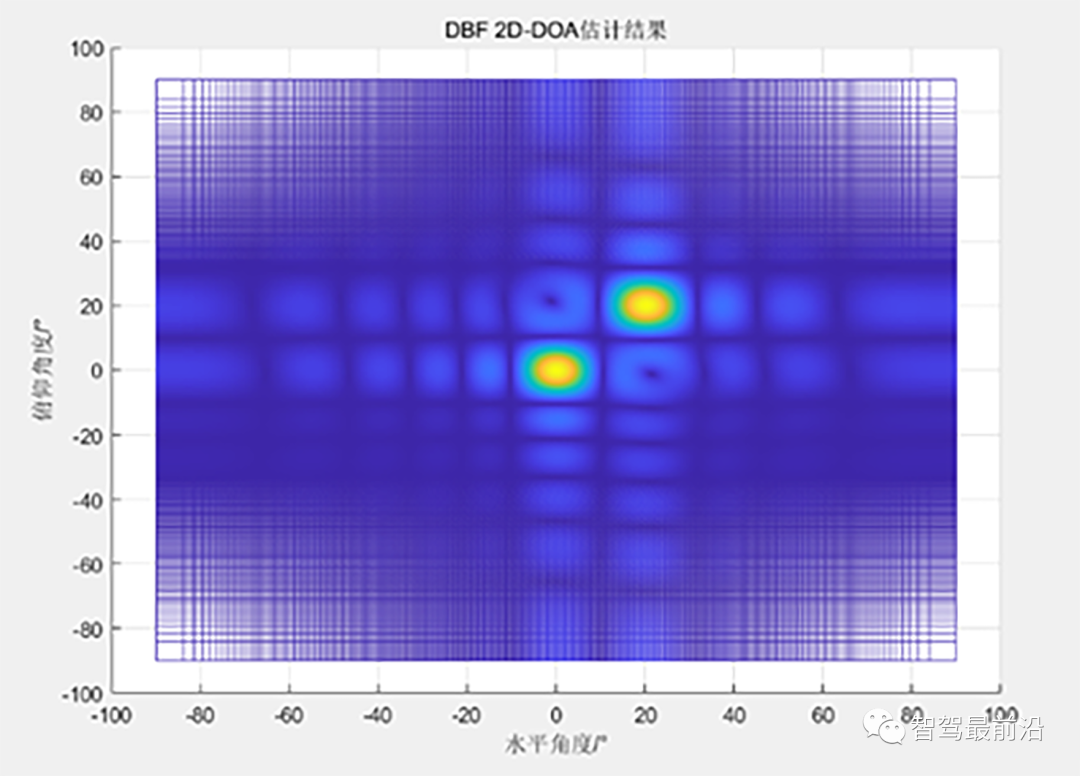
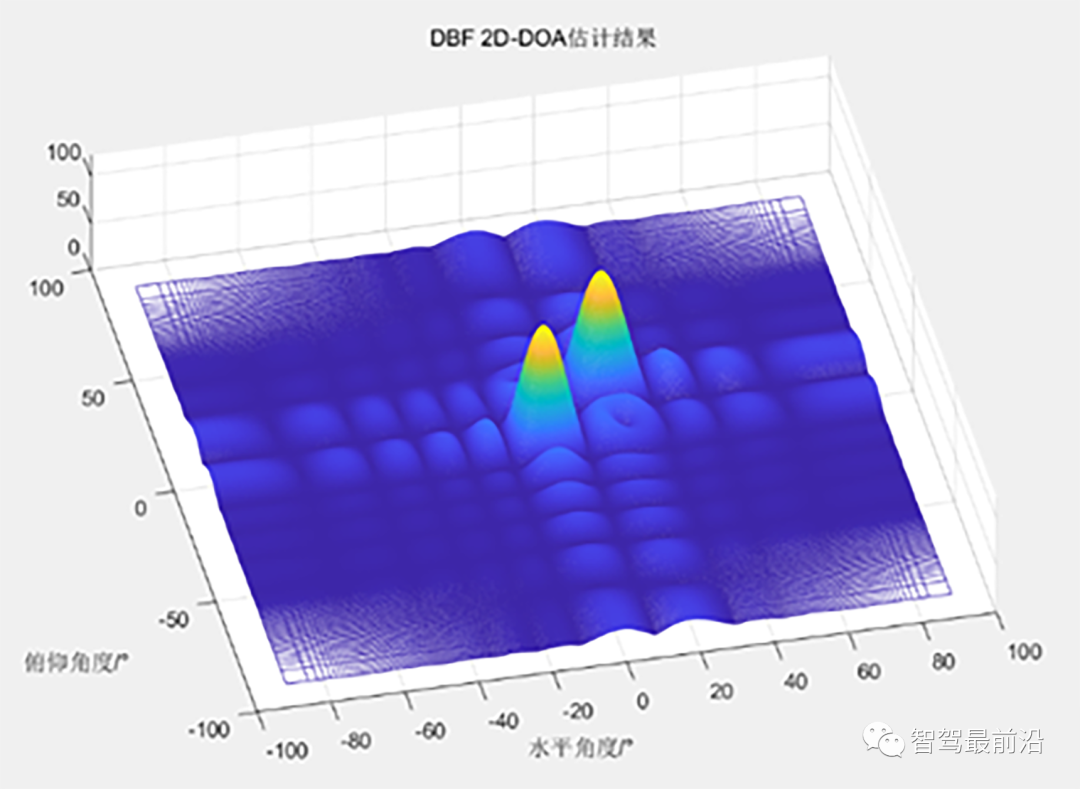
10*10的二维虚拟面阵仿真结果 目标在（0°，0°）、（20°，20°）的位置，可以看到当我们找到二维压缩后的矩阵中的两个极值点时，也就能直接得到该目标的二维角度值。不过在实际应用中，我们并不需要直接先二维压缩之后再在该面阵中找极值点，而是先进行其中一个维度的压缩，从这一维度的压缩结果中得到目标在该维度的角度值，随后只在有目标的索引值对应的行/列上进行另一维度的压缩以完成目标的二维角度测量。

2、需要进行角度匹配

对于二维的矩形面阵，直接使用前面的方法是最优的，计算简单，没有复杂的匹配算法，信噪比和动态范围都较高。但是从角度测量的角度来看，面阵其实有大量的信息冗余，我们其实并不需要一个完整的二维矩形面阵来得到目标的二维角度，我们可以很大程度上减少天线的使用，但是做任何事情都是有代价的，这样做的代价是：需要设计更复杂的阵列以及需要用到更复杂的算法。 加特兰在其baseband中提出了一种角度匹配思路，但是具体如何进行角度匹配的没有做细节说明，下文给出一种类似的方法。为方便叙述和理解，我还是基于面阵来做说明。

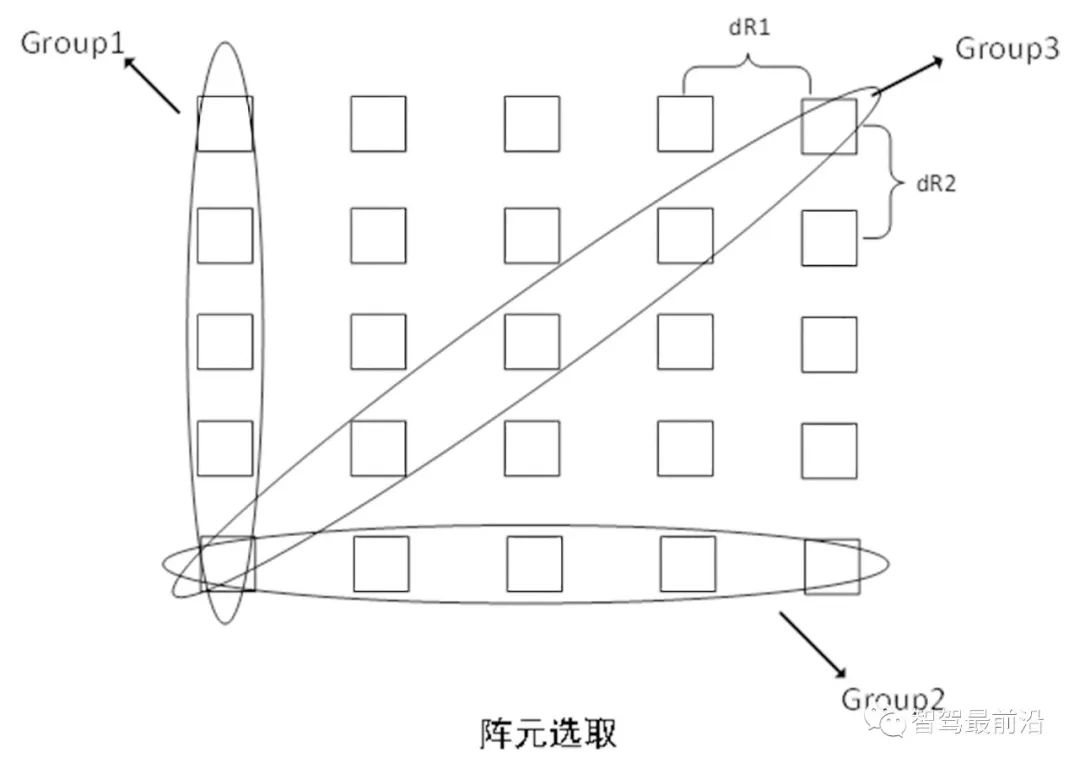
如上图所示，对于该二维矩形面阵，我们只要选取其中三列的数据来做目标的二维角度估计。对这三个group的数据分别使用FFT或者波束成形的方法对数据进行处理，可以使用找极值等方法得到目标可能的角度(三个角度group)，比如：Group1对应得到的角度为：α = （α1， α2， α3），Group2对应得到的角度为：β = (β1，β2，β3)，Group3对应的角度为：γ = (γ1，γ2，γ3)。α为三个目标水平方向的角度，β为三个目标竖直方向的角度，我们目前还无法确定它们之间的对应关系，但γ中包含了目标水平和竖直向的相关信息，我们可以基于如下关系完成α与β之间的匹配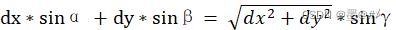： 当选取斜对角线对应的阵元作为Group3时，上式中dx = dR1，dy = dR2。将三个group得到的角度信息代入上述关系式，便可以完成目标水平向和竖直向的角度匹配。

3、补充

二维角度关联的方法有很多，比如还有阵列矩阵先向量化再进行角度估计等方法(博主这边能跑通代码但是原理理解得不是很深刻暂时不表)。需要进行角度关联的操作时一般对阵列设计有一定的要求。  

总结

本篇博文对毫米波雷达的DOA估计做了一个较为全面的概述，给出了包括DBF、FFT、Capon、Music、DML、ESPRIT、OMP、IAA等测角算法的基本介绍、仿真效果、以及应用的条件和对比。博文还探讨了4D毫米波雷达的实现路线、2D-DOA估计方法等问题。  

编辑：黄飞