

为什么说数据结构很重要2
电子说
描述
3.插入
往数组里插入一个新元素的速度,取决于你想把它插入到哪个位置上。
假设我们想要在购物清单的末尾插入"figs"。那么只需一步。因为之前说过了,计算机知道数组开头的内存地址,也知道数组包含多少个元素,所以可以算出要插入的内存地址,然后一步跳到那里插入就行了。图示如下。
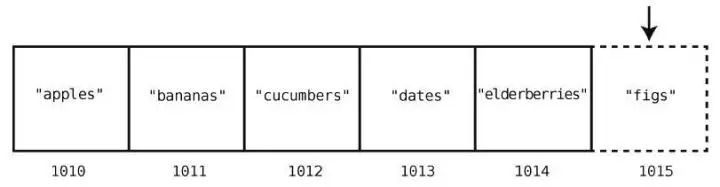
但在数组开头或中间插入,就另当别论了。这种情况下,我们需要移动其他元素以腾出空间,于是得花费额外的步数。
例如往索引2 处插入"figs",如下所示。

为了达到目的,我们必须先把"cucumbers"、"dates"和"elderberries"往右移,以便空出索引2。而这也不是一步就能移好,因为我们首先要将"elderberries"右移一格,以空出位置给"dates",然后再将"dates"右移,以空出位置给"cucumbers",下面来演示这个过程。
第1 步:"elderberries"右移。

第2 步:"date"右移。

第3 步:"cucembers"右移。

第4 步:至此,可以在索引2 处插入"figs"了。

如上所示,整个过程有4 步,开始3 步都是在移动数据,剩下1 步才是真正的插入数据。
最低效(花费最多步数)的插入是插入在数组开头。因为这时候需要把数组所有的元素都往右移。于是,一个含有N 个元素的数组,其插入数据的最坏情况会花费N + 1 步。即插入在数组开头,导致N 次移动,加上一次插入。
最后要说的“删除”,则相当于插入的反向操作。
4.删除
数组的删除就是消掉其某个索引上的数据。
我们找回最开始的那个数组,删除索引2 上的值,即"cucumbers"。
第1 步:删除"cucumbers"。
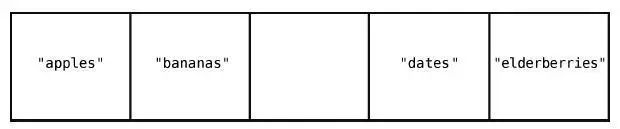
虽然删除"cucumbers"好像一步就搞定了,但这带来了新的问题:数组中间空出了一个格子。因为数组中间是不应该有空格的,所以,我们得把"dates"和"elderberries"往左移。
第2 步:将"dates"左移。

第3 步:将"elderberries"左移。

结果,整个删除操作花了3 步。其中第1 步是真正的删除,剩下的2 步是移数据去填空格。
所以,删除本身只需要1 步,但接下来需要额外的步骤将数据左移以填补删除所带来的空隙。
跟插入一样,删除的最坏情况就是删掉数组的第一个元素。因为数组不允许空元素,当索引0 空出,那么剩下的所有元素都要往左移去填空。
对于含有5 个元素的数组,删除第一个元素需要1 步,左移剩余的元素需要4 步。而对于500个元素的数组,删除第一个元素需要1 步,左移剩余的元素需要499 步。可以推出,对于含有N个元素的数组,删除操作最多需要N 步。
既然学会了如何分析数据结构的时间复杂度,那就可以开始探索各种数据结构的性能差异了。了解这些非常重要,因为数据结构的性能差异会直接造成程序的性能差异。
下一个要介绍的数据结构是集合,它跟数组似乎很像,甚至让人以为就是同一种东西。然而,我们将会看到它跟数组在性能上是有区别的。
集合:一条规则决定性能
来看看另一种数据结构:集合。它是一种不允许元素重复的数据结构。
其实集合是有不同形式的,但现在我们只讨论基于数组的那种。这种集合跟数组差不多,都是一个普通的元素列表,唯一的区别在于,集合不允许插入重复的值。
要是你想往集合["a", "b", "c"]再插入一个"b",计算机是不会允许的,因为集合中已经有"b"了。
集合就是用于确保数据不重复。
如果你要创建一个线上电话本,你应该不会希望相同的号码出现两次吧。事实上,现在我的本地电话本就有这种状况:我家的电话号码不单指向我这里,还错误地指向了一个叫Zirkind 的家庭(这是真的)。接听那些要找Zirkind 的电话或留言真的挺烦的。
不过,估计Zirkind 一家也在纳闷为什么总是接不到电话。而当我想要打电话告诉Zirkind 号码错了的时候,我妻子就会去接电话了,因为我拨的就是我家号码(好吧,这是开玩笑)。如果这个电话本程序用集合来处理,那就不会搞出这种麻烦了。
总之,集合就是一个带有“不允许重复”这种简单限制的数组。而该限制也导致它在4 种基本操作中有1 种与数组性能不同。
下面就来分析读取、查找、插入和删除在基于数组的集合上表现如何。
集合的读取跟数组的读取完全一样,计算机只要一步就能获取指定索引上的值。如之前解释的那样,这是因为计算机知道集合开头的内存地址,所以能够一步跳到集合的任意索引。
集合的查找也跟数组的查找无异,需要N 步去检查某个值在不在集合当中。删除也是,总共需要N 步去删除和左移填空。
但插入就不同了。先看看在集合末尾的插入。对于数组来说,末尾插入是最高效的,它只需要1 步。
而对于集合,计算机得先确定要插入的值不存在于其中——因为这就是集合:不允许重复值。
于是每次插入都要先来一次查找。
假设我们的购物清单是一个集合——用集合还是不错的,毕竟你不会想买重复的东西。如果当前集合是["apples", "bananas", "cucumbers", "dates", "elderberries"],然后想插入"figs",那么就需要做一次如下的查找。
第1 步:检查索引0 有没有"figs"。
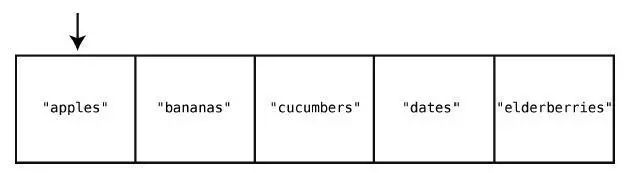
没有,不过说不定其他索引会有。为了在真正插入前确保它不存在于任何索引上,我们继续。
第2 步:检查索引1。

第3 步:检查索引2。

第4 步:检查索引3。

第5 步:检查索引4。
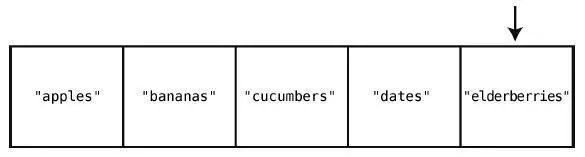
直到检查完整个集合,才能确定插入"figs"是安全的。于是,到最后一步。
第6 步:在集合末尾插入"figs"。
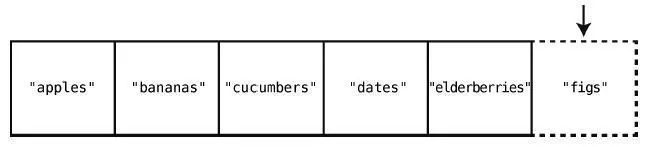
在集合的末尾插入也属于最好的情况,不过对于一个含有5 个元素的集合,你仍然要花6 步。因为,在最终插入的那一步之前,要把5 个元素都检查一遍。
换句话说,在N 个元素的集合中进行插入的最好情况需要N + 1 步——N 步去确认被插入的值不在集合中,加上最后插入的1 步。
最坏的情况则是在集合的开头插入,这时计算机得检查N 个格子以保证集合不包含那个值,然后用N 步来把所有值右移,最后再用1 步来插入新值。总共2N + 1 步。
这是否意味着因为它的插入比一般的数组慢,所以就不要用了呢?当然不是。在需要保证数据不重复的场景中,集合是非常重要的(真希望有一天我的电话本能恢复正常)。但如果没有这种需求,那么选择插入比集合快的数组会更好一些。具体哪种数据结构更合适,当然要根据你的实际应用场景而定。
总结
理解数据结构的性能,关键在于分析操作所需的步数。采取哪种数据结构将决定你的程序是能够承受住压力,还是崩溃。本文特别讲解了如何通过步数分析来判断某种应用该选择数组还是集合。
-
数据结构2017-03-04 3288
-
请问数据结构对弄单片机重要吗?2019-04-12 2196
-
数据结构的几个重要知识点2020-02-27 2015
-
常见的数据结构2020-05-10 2627
-
数据结构教程,下载2009-05-14 661
-
什么是数据结构2009-08-13 1905
-
数据结构在游戏编写中的应用2011-07-25 768
-
数据结构与算法分析—C语言描述2015-11-18 658
-
数据结构与算法2016-03-30 622
-
数据结构是什么_数据结构有什么用2017-11-17 16567
-
为什么要学习数据结构?数据结构的应用详细资料概述免费下载2018-09-11 1346
-
什么是数据结构?为什么要学习数据结构?数据结构的应用实例分析2018-09-26 1472
-
大牛分享平时如何学习数据结构与算法2018-11-02 3492
-
JavaScrit数据结构与算法(第2版)2021-06-01 721
-
为什么说数据结构很重要12023-04-06 1015
全部0条评论

快来发表一下你的评论吧 !

