电机绕组：几种不同形式的分数槽绕组对称条件

本期讲分数槽绕组的对称条件和并联支路数。

1 分数槽绕组的对称条件

对于整数槽绕组，由于每极每相槽数为整数，每极每相的槽数相等，总是能够构成对称的多相绕组，不存在绕组不对称的问题。但对于分数槽绕组，由于每个相带的槽数不相等，如果极槽配合不当，可能无法构成对称的多相绕组，极槽配合必须要满足一定的条件才能构成对称的多相绕组。

关于分数槽绕组的对称条件，有许多表达形式，不同文献上讲的对称条件也不同，但都是从不同角度推导出来的结果，表达方式不同而已，其本质是等效的，满足一种形式的对称条件，其它也必然满足。接下来我们就介绍几种不同形式的分数槽绕组对称条件。

构成对称多相绕组的条件有两个：第一个对称条件就是每相绕组的线圈个数必须相等；第二个对称条件是各相绕组在定子圆周上的分布必须均匀，即相邻两相绕组的轴线夹角相等，每相绕组产生的电势和磁势要对称。两个条件必须同时满足才能构成对称多相绕组。下面我们分别讲解这两个对称条件。

1.1 第一个对称条件

如上所述，构成对称多相绕组的第一个条件是每相绕组的线圈个数必须相等，这个条件应该很好理解，如果每相绕组的线圈不相等，那么就谈不上对称。设定子槽数为Z1，相数为m，极对数为p，每极每相槽数为q，则对于单层绕组来说，定子Z1个槽就一共有Z1/2个线圈，要想每相绕组线圈个数相等，这Z1/2个线圈就必须能够被相数m整除，即对于单层绕组，第一个对称条件为：

Z1/(2m)=pq=整数 (1)

对于双层绕组，Z1个槽一共就有Z1个线圈，要想每相绕组线圈个数相等，这Z1个线圈就必须能够被相数m整除，即对于双层绕组，第一个对称条件为：

Z1/m=2pq=整数 (2)

由⑴、⑵式可见，整数槽绕组总是可以满足第一对称条件的，因为整数槽绕组的p和q都是整数，二者相乘当然还是整数。

对于分数槽绕组，由于q=N/d为一个不可约的分数，对单层分数槽绕组，第一个对称条件：Z1/(2m)=pq=p•(N/d)=整数，由于N与d不能整除，要想满足该条件，必须p与d能够整除，即对于分数槽单层绕组，第一个对称条件可演化为：

p/d=整数                                    (3)

同理对于双层分数槽绕组的第一个对称条件可演化为：

2p/d=整数                                    (4)

比较⑶、⑷式可见，双层绕组比单层绕组更容易满足第一个对称条件，在设计时双层绕组具有更多的极槽配合选择余地。

1.2 第二个对称条件

第二个对称条件是每相绕组的布置要对称，各相绕组产生的电势和磁势分布要对称。这个条件进一步推论一下就是各相电势之间的相位差均匀，或每相绕组的相带宽度要相等。可以从不同的角度入手来推导出第二个对称条件。

1.2.1 从槽电势星型图推导第二个对称条件

槽电势星型图反映了各槽电势或者说各线圈电势的相位关系，每个单元电机对应一个槽电势星型图，各单元电机的槽电势星型图是重叠，我们把一个单元电机对应的槽电势星型图称为基本星型图，由于各单元电机的槽电势星型图是重叠的，因此只要研究一个单元的槽电势星型图，其它单元电机即可简单复制。一个基本星型图里包含许多个槽电势相量，要想使多相绕组对称，必须要把基本星型图上的相量个数能够平均分配给每一相，也就是说，基本星型图中的相量个数必须能够被相数整除。基于此即可推出构成对称多相绕组的第二个条件为：

Z′=Z0/m=(Z1/t)/m=Z1/(m•t)=整数 (5)

式中：Z′为每个单元电机每相分得的槽数，或者说一个基本星型图内每相包括的相量个数；Z0为单元电机的槽数，或者叫基本星型图中的相量总个数；m为相数；Z1为定子总槽数；t为单元电机个数，即Z1与极对数p的最大公约数。

显然对于整数槽绕组，由于t=p，⑸式永远是满足的，因此整数槽绕组总是能够构成对称多相绕组。

对于分数槽绕组，需要根据给出的电机总槽数Z1，极对数p，相数m，分两步判断是否能够构成对称绕组：第一步，首先求出总槽数Z1与极对数p的最大公约数t；第二步，根据⑸式计算Z1/(m•t)看是否能够整除，如果能够整除就可以构成对称多相绕组，否则不能构成对称多相绕组。

1.2.2 从相带宽度推导第二个对称条件

一个基本星型图中的相量个数为Z0=Z1/t，则相邻两个相量之间的相位差(即相距角)：

α′=360º/Z0=360•t/Z1  (6)

对于m相对称绕组，每相的相带宽度为：

αφ=360º/m                               (7)

要想构成m相对称绕组，则一个相带内必须包括整数个槽电势相量，即相带宽度αφ必须要能被相距角α′整除，即：

αφ/α′=(360º/m)/(360•t/Z1)=Z1/(m•t)=整数 (8)

式⑻即为从相带划分的角度推导出的对称条件，比较⑻式和⑸式可见，两式是一样的。只不过是从不同的角度入手，推导出了同样的结果。

1.2.3 用每极每相槽数q来判断对称条件

以上从两个不同角度入手，推导出了同样的构成多相绕组的对称条件，即：

Z1/(m•t)=整数 (9)

用这个对称条件来判断一个分数槽的极槽配合能否构成多相对称绕组固然是可以的，但判断时需要分两步，先求出Z1与p的最大公约数t，再用⑼式判断是否能够构成对称绕组，这样不仅比较麻烦，而且也不易记忆。实践中常用另外一种简单的判别方法，即用每极每相槽数q的分母d来判断是否能够构成多相对称绕组。这里先把结果告诉大家，这个判别方法就是：看每极每相槽数q的分母d是否能被相数m整除，如果能够整除就不能构成多相对称绕组；如果不能整除就能够构成多相对称绕组。即构成多相对称分数槽绕组的条件为：

d/m≠整数                                   (10)

对于三相绕组，就是d不能被3整除。其实(10)式也是从(9)式推导而来的，二者是等效的。接下来就用两种方法来证明这个对称条件。

【证法Ⅰ】设每极每相槽数：

q=b+c/d=(bd+c)/d

则：

Z′=Z1/(m•t)=2p•m•q/(m•t)=(2p/t)•q=(2p/t)•(bd+c)/d=整数 (11)

由于(bd+c)/d是除不尽的分数，要想满足(11)式，只有2p/t能够被d整除。又由于t是Z1与p的最大公约数，所以Z1=m•t•Z′与p=(p/t)•t之间除了最大公约数t之外，p/t与m之间不能再有不是1的公约数，另外由于多相电机m＞2，所以2p/t也不能被m整除。综上，要想满足(11)式，必须2(p/t)能被d整除，而2(p/t)不能被m整除，所以d也不能被m整除。

【证法Ⅱ】设每极每相槽数：

q=b+c/d=(bd+c)/d=N/d (12)

则：

Z1=2mpq=2mpN/d (13)

p=d•(p/d)                   (14)

由第一个对称条件⑶式可知，p/d=整数，根据(13)、(14)式，这个整数p/d显然是Z1与p的一个公约数，又由于N和d不可约，Z1和p的其它公约数只能包含于2m和d中，换句话说，Z1和p的其它公约数必定也是2m和d的公约数，设这些其它公约数为k，则Z1和p的最大公约数(单元电机个数)即为：

t=k•(p/d)                             (15)

将(13)、(15)式代入⑼式中，得第二个对称条件为：

Z1/(mt)=(2mpN/d)/(mkp/d)=2N/k=整数 (16)

由于d的约数k不能是N的约数，因此k只能是1或2。也就是说在2m和d中只可能有1和2两个公约数，无论是1还是2，对多相电机(m＞2)，d和m都不会有大于2的公约数，即第二个对称条件为：

d/m≠整数                                 (17)

对于三相电机：

d/3≠整数                                 (18)

以上用两种方法证明了构成对称多相绕组的条件。再次将两个对称条件重复如下：

对单层分数槽绕组：

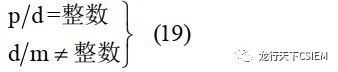
  对于双层分数槽绕组：

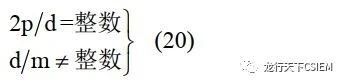
  由以上两式可见，对于三相(m=3)分数槽电机，如果极对数为3的倍数次方(p=3、9、27…)，则绝对不能满足式(19)的条件，因此这种极对数的分数槽电机是绝对不能构成单层三相分数槽绕组的。

2 分数槽绕组的并联支路数

能够构成并联支路的条件是支路中包含的线圈电势叠加后的大小和相位都相同才能被并联起来。对于分数槽绕组分两种情况，第一种情况：如果一个单元电机中每相槽数是奇数，则不能等分成两个相等的正负相带，这种情况下只能构成双层绕组，且一个单元电机只能构成一条并联支路，t个单元电机最多可以构成t条并联支路。第二种情况：如果一个单元电机中每相槽数是偶数，则可以等分成两个相等的正负相带，这种情况下对于双层绕组，一个单元电机中可以构成两条并联支路，t个单元电机最多可以构成2t条并联支路；这种情况也可以构成单层绕组，一个单元只能构成一条并联支路，t个单元电机最多可以构成t条并联支路(后面会提到有特例)。接下来我们就分这两种情况，分别介绍分数槽绕组的并联支路数。

2.1 当Z′为奇数时的最大并联支路数

分数槽绕组一个单元电机中每相的槽数为Z′=Z1/t•m。

则每极每相槽数：

q=Z1/(2pm)=Z′•t•m/(2pm)=Z′/(2p/t)=Z′/(2p′)=N/d (21)

其中：Z′=Z0/m；Z0=Z1/t为每个单元电机的槽数；p′=p/t为每个单元电机的极对数。由于t为Z1与p的最大公约数，故Z0和p′不可约，因此Z′与p′也不可约，又由于Z′为奇数，故Z′与2也不可约，因此Z′与2p′必不可约，即Z′/2p′为最简分数，那必然是N=Z′；d=2p′=2p/t。由此可见，单元电机个数为：

t=2p/d                                (22)

Z′为奇数，即一个单元电机中每相槽数为奇数，不能等分成两个相等的正负相带，因此这种情况只能构成双层绕组，且一个单元电机只能一条并联支路，t个单元电机最多可以构成t条并联支路。即这种情况的最大并联支路数为：

amax=t=2p/d                             (23)

由于用Z′的奇偶作为判别条件需要复杂的计算，不太简便和直观，分数槽绕组通常都是先算出每极每相槽数q，这样其分母d自然就知道奇偶，因此实践中常用d的奇偶作为判别条件。由式(21)可见，当一个单元电机中每相的槽数Z′=N为奇数时，d=2p/t必为偶数，因此上述Z′为奇数的前提条件可以转化为d为偶数。

小结一下：当d为偶数时，只能构成双层分数槽绕组，其最大并联支路数为2p/d。

2.2 当Z′为偶数时的最大并联支路数

如果Z′为偶数，则每极每相槽数：

q=Z1/(2pm)=Z′•t•m/(2pm)=(Z′/2)/(p/t)=(Z′/2)/p′=N/d (24)

同理，由于Z′与p′不可约，Z′/2与p′必不可约，即(Z′/2)/p′为最简分数，那必然是N=Z′/2；d=p′=p/t，则单元电机个数为：

t=p/d                                   (25)

另外由于Z′与p′不可约，Z′为偶数时，p′必为奇数，因此也可以把Z′为偶数的前提条件转化为d为奇数。即d为奇数时，可以把每相等分成两个相等的正负相带，此时即可以构成双层绕组，也可以构成单层绕组。

如果是双层绕组，一个单元电机可以构成两条并联支路，t个单元电机最多可以构成2t条并联支路，即这种情况对双层绕组最大并联支路数为：

amax=2t=2p/d                             (26)

如果是单层绕组，一个单元只能构成一条并联支路，t个单元电机最多可以构成t条并联支路，即这种情况对单层绕组最大并联支路数为：

amax=t=p/d                              (27)

另外，这种情况还存在一种特例，就是如果Z′能够被4整除，也就是N为偶数时，则一个单元电机内仍然可以将每个正相带和负相带的槽数再平分成两份，两份槽内导体在端部分别向两边跨接构成单层绕组的两条并联支路，t个单元电机，就能够构成最大并联支路数为2t的单层绕组，即此时最大并联支路数为：

amax=2t=2p/d                             (28)

这种特例情况类似q为偶数的整数槽绕组，采用链式接法时仍然可以构成最大并联支路数为2p的单层绕组，有关详细论述参见《电机绕组(2)》中的示例二和示例三，这里不再赘述。

小结一下：当d为奇数时，即可以构成双层分数槽绕组，也可以构成单层分数槽绕组。构成双层绕组时，其最大并联支路数为2p/d；构成单层绕组时，如果N为奇数则最大并联支路数为p/d；如果N为偶数，则最大并联支路数为2p/d。

2.3 分数槽绕组最大并联支路数总结

综上所述，由式(23)、(26)、(27)、(28)可以得出以下结论：

【结论Ⅰ】无论d为偶数还是奇数，都可以构成双层绕组，双层分数槽绕组的最大并联支路数都是2p/d。

【结论Ⅱ】只有d为奇数时，才可以构成单层绕组。构成单层绕组时，如果N为偶数，则最大并联支路数仍为2p/d；如果N为奇数则最大并联支路数为p/d。

2.4 分数槽绕组的实际并联支路数

以上论述的是分数槽绕组可能构成的最大并联支路数，实际电机中的并联支路数a可以少于上述最大并联支路数amax，但必须是最大并联支路数的约数，即：

amax/a=整数                                 (29)

上述介绍了分数槽绕组的对称条件和并联支路数，以上分析可见，虽然就这么几个数字倒腾过来倒腾过去，用的都是些小学数学知识，但消化起来还是很烧脑子的，想深入消化理解的同学们一定要静下心来，多看几遍慢慢理解，不想烧脑子的同学们看不懂也没关系，你就记住文中的那些结论和结论性的判别式即可快速判断极槽配合能否构成对称分数槽绕组，能够构成几路并联。

编辑：黄飞