评估低抖动PLL时钟发生器的电源噪声抑制

本文讨论电源噪声干扰对基于PLL的时钟发生器的影响，并介绍几种用于评估由此产生的确定性抖动（DJ）的测量技术。派生关系显示了如何使用频域杂散测量来评估时序抖动行为。实验室台架测试结果用于比较测量技术，并演示如何可靠地评估参考时钟发生器的电源噪声抑制（PSNR）性能。

采用PLL的时钟发生器广泛用于网络设备中，用于生成高精度和低抖动参考时钟或保持同步网络操作。大多数时钟振荡器使用理想、干净的电源给出其抖动或相位噪声规格。然而，在实际的系统环境中，电源可能会因板载开关电源或嘈杂的数字ASIC而受到干扰。为了在系统设计中实现最佳性能，了解这种干扰的影响非常重要。

首先，我们将研究基于PLL的时钟发生器的基本电源噪声抑制（PSNR）特性。然后，我们将解释如何从频域测量中提取时序抖动信息。然后应用这些技术，并使用实验室台架测试比较几种不同的测量方法。最后，我们将总结首选方法的优点。

PLL时钟发生器的PSNR特性

典型的PLL时钟发生器如图1所示。由于输出驱动器对于不同类型的逻辑接口可能具有非常不同的PSNR性能，因此以下分析将重点介绍电源噪声对PLL本身的影响。

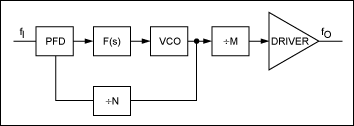
图1.PLL时钟发生器的典型拓扑。

图2显示了PLL相位模型。该模型假设电源噪声为 VN，注入 PLL/VCO，并且分频比 M 和 N 设置为 1。

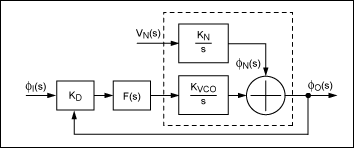
图2.锁相环的相位模型。

从VN（s）到ΦO（s）的PLL闭环传递函数由下式给出：

这里 ω3分贝是 PLL 3dB 带宽，ΩZ是PLL零点频率，ωZ<< ω3分贝.

公式3表明，在PLL时钟发生器中，当电源干扰（PSI）频率大于PLL20dB带宽时，电源噪声抑制3dB/dec。对于 ω 之间的 PSI 频率Z和 ω3分贝，输出时钟相位随PSI幅度变化，如下所示：

例如，图3显示了PLL在PLL的3dB带宽的两种不同设置下的PSNR特性。

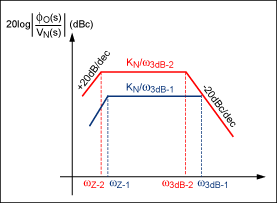
图3.典型的 PLL PSNR 特性。

功率频谱杂散到DJ的转换

当单音正弦信号时，fM，应用于PLL的电源，它在时钟输出端产生窄带相位调制。这种相位调制通常可以用傅里叶级数表示来描述：

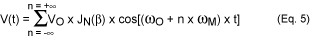
这里β是表示最大相位偏差的调制指数。对于小折射率调制（β << 1），贝塞尔函数可以近似为：

这里 n = 0 表示载体本身。当n = ±1时，相位调制信号由下式给出：

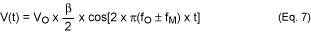
测量双边带功率谱SV（f）时，如果变量x表示fO处载波与fM处基波边带音之间的电平差，则：

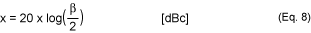
由于β是以弧度为单位的最大相位偏差，因此由这种小折射率相位调制引起的峰峰值DJ可以推导出为：

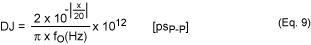
上述分析假设没有幅度调制对fM音调的影响。实际上，幅度和相位调制都可以产生，从而降低了这种方法的精度。

将相位噪声频谱杂散转换为DJ

有一种方法可以在测量功率谱S 时避免调幅效应V（f）.可以通过测量相位噪声频谱中的杂散来计算DJ，同时在电源上施加单音正弦干扰。变量y（dBc）表示在频率偏移f下测得的单边带相位杂散功率M，产生的相位偏差ΔΦ（rad有效值） 可以派生为：

 

需要注意的是，上述分析中的单边带相位谱并不是双边带谱的折叠版本。这就是公式3中10dB分量的原因。图4显示了DJ与公式12给出的相位杂散功率之间的关系。

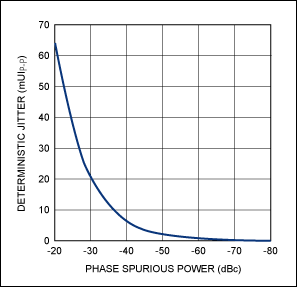
图4.DJ 与相位杂散功率。

PSNR测量技术

下一节将演示测量时钟源PSNR的五种不同方法。MAX3624低抖动时钟发生器作为示例。图5所示的测量设置使用函数发生器将正弦信号注入MAX3624评估（EV）板的电源。单音干扰的幅度直接在V处测量抄送引脚靠近 IC。限幅放大器MAX3272用于消除幅度调制;随后是一个巴伦，将差分输出转换为单端信号，用于驱动不同的测试设备。为了比较不同测试的结果，所有测量均在以下条件下进行：

时钟输出频率：fO= 125兆赫

正弦调制频率：fM= 100kHz

正弦信号幅度：80mVP-P

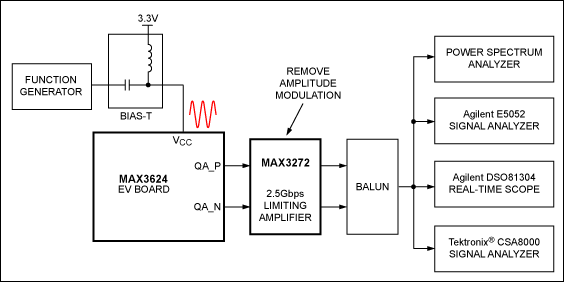
图5.PSNR 测量设置。

方法 1.功率谱测量

在功率频谱分析仪上观察时，窄带相位调制表现为载波周围的两个边带。图 6 显示了使用安捷伦 E5052 的频谱监控器功能查看时的情况。测得的第一边带幅度相对于载波幅度为-53.1dBc，换算为11.2ps®P-PDJ，根据公式 9。

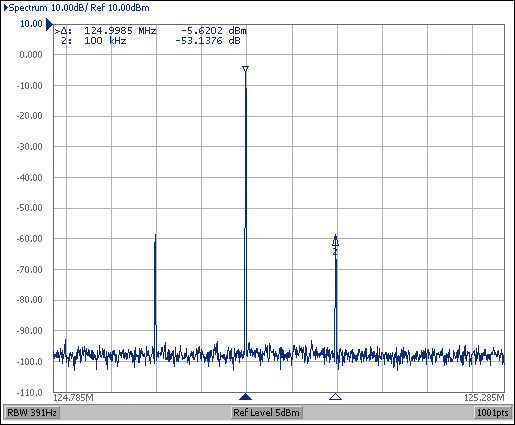
图6.测量的功率谱。

方法 2.SSB 相位杂散测量

在相位噪声分析仪上，PSI将表现为相对于载波的相位杂散。测得的相位噪声频谱如图7所示。100kHz时的相位杂散功率为-53.9dBc，相当于10.2psP-PDJ使用公式12。

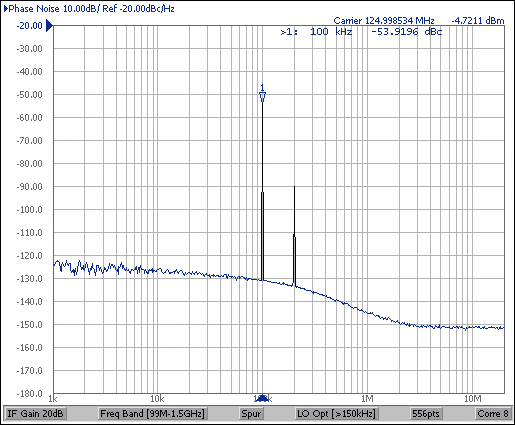
图7.测量的SSB相位噪声和杂散。

方法 3.相位解调测量

使用 Agilent E5052 信号分析仪，可直接测量 100kHz 处的相位解调正弦信号，如图 8 所示，给出了与其理想位置的最大相位偏差。峰峰值相位偏差为0.47°，换算为10.5psP-P在 125MHz 的输出频率下。

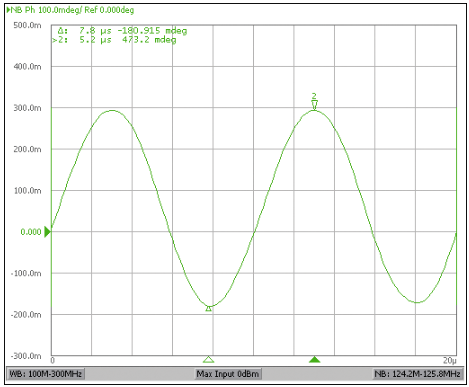
图8.MAX3624相位解调信号

方法 4.实时示波器测量

在时域测量中，PSI引起的DJ可以通过测量时间间隔误差（TIE）直方图来获得。在实时示波器上，当单音干扰注入PLL时，时钟输出TIE分布将显示为正弦概率密度函数（PDF）。DJ 可以使用双狄拉克模型¹ 通过测量 TIE 直方图中两个高斯分布的平均值之间的峰值距离来估计。图 9 显示了使用安捷伦无限 DSO81304A 40GSa/s 实时示波器测得的 TIE 直方图。测得的峰分离为9.4ps。

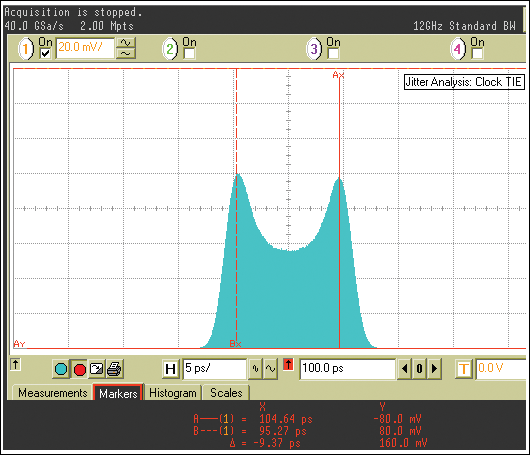
图9.测量的 TIE 直方图。

应该注意的是，实时示波器的存储深度可能会限制可应用于PLL电源的低正弦调制频率。例如，如果测试设备的存储深度在采样率设置为2Gsps时为40Msps，则它只能捕获低至20kHz的抖动频率分量。

方法 5.采样范围测量

使用采样示波器时，需要同步触发信号来分析被测时钟抖动。TIE测量可以使用两种触发方法。

第一种方法是将低抖动参考时钟应用于PLL时钟发生器的输入;使用与采样示波器触发器相同的时钟源。图10a显示了测得的TIE直方图，其峰值间距为9.2ps。使用参考时钟触发的优点是，测得的TIE直方图峰间距与触发位置的水平时间延迟无关。但是，测得的TIE直方图可能会受到触发时钟抖动的影响。因此，使用抖动比被测时钟发生器器件低得多的时钟源非常重要。

替代方法使用自触发来消除触发时钟抖动的影响。在这种情况下，被测时钟发生器的输出使用功率分配器分成两个相同的信号。一个信号施加到采样示波器的数据输入，另一个信号施加到触发输入。由于触发信号包含与测试信号相同的DJ，因此当示波器主时基的水平位置扫过正弦调制频率的一个周期时，直方图峰值分离会发生变化。在调制信号半个周期的水平位置，TIE直方图上的峰值间隔将是测试信号的两倍。图10b所示为水平时延设置为3624μs时测得的MAX5 TIE直方图。估计的TIE峰值分离为19ps，相当于9.5ps的DJP-P.

图10c显示了在与触发点不同的水平时间延迟下测得的TIE直方图峰间距。为了进行比较，当采样范围由参考时钟输入触发时，也会显示TIE结果。

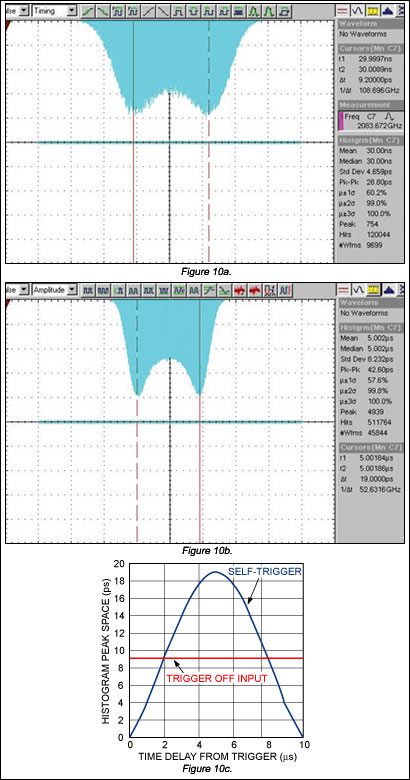
图 10.TIE 直方图显示了各种触发条件：由REF_IN （a） 触发;自触发，Td= 5μs （b）;以及峰值间距与触发时间延迟的关系 （c）。

测量摘要

表1总结了MAX3624 125MHz时钟输出端测得的DJ。使用上面讨论的不同方法收集数据。应该注意的是，使用TIE直方图的双狄拉克近似测量的DJ略小于从频域频谱分析中获得的DJ。这种差异是由正弦抖动 （SJ） PDF 与随机抖动分量的高斯分布卷积过程引起的。 因此，从双狄拉克模型中提取的 DJ 只是一个估计值;仅当随机抖动的标准偏差远小于抖动直方图的两个峰值间隔之间的距离时，才应应用它。

 

测量方法	DJ （psP-P)
功率谱	11.2
SSB 相位杂散	10.3
相分解	10.5
实时范围	9.4
采样范围 （参考触发）	9.2
采样范围 （自触发）	9.5
*80mVP-P，电源上的100kHz正弦信号。

 

结论

对于示例中使用的相对较大的干扰，结果具有很好的相关性。但是，当干扰水平相对于随机抖动下降时，时域方法变得不那么精确。此外，如果时钟信号被幅度调制破坏，则使用功率谱分析仪的测量将变得不可靠。因此，在所介绍的所有方法中，使用相位噪声分析仪测量相位杂散功率是表征时钟发生器PSNR的最准确、最方便的方法。相同的方法可以扩展为评估由相位噪声频谱上出现的其他杂散产物引起的DJ方面。

审核编辑：郭婷