PWM逆变电路谐波分析

前面我们聊了PWM(脉冲宽度调制)的基本概念和原理，今天我们来聊一聊PWM逆变电路的谐波，及PWM逆变电路中如何提高直流电压利用率以及减少开关次数。

1PWM逆变电路谐波分析

载波对正弦信号波调制，会产生和载波有关的谐波分量，这些谐波分量的频率和幅值是衡量PWM逆变电路性能的重要指标之一。

同步调制我们可以看成异步调制的特殊情况，所以我们只分析异步调制方式的谐波。 以载波周期为基础，再利用贝塞尔函数可以推导出PWM波的傅里叶级数表达式。 这种分析方法的过程相当复杂，但是结论却是简单而又直观的。

单相桥式PWM逆变电路

输出电压频谱图如下：

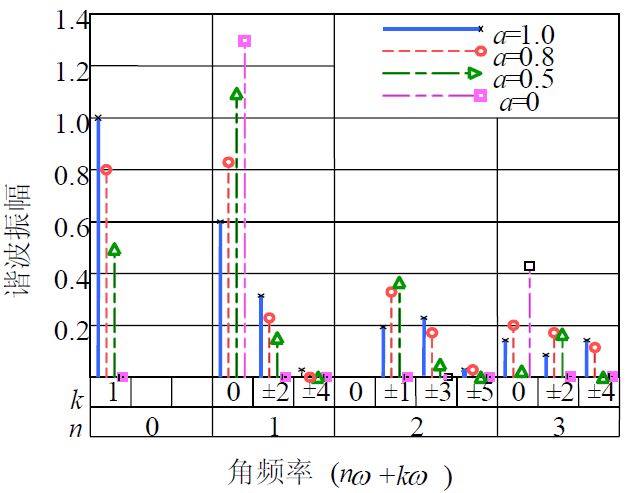
所包含的谐波角频率为

nωc±kωr

式中，n=1,3,5,... 时，k=0,2,4,...; n=2,4,6,... 时，k=1,3,5,...

其PWM波中不含有低次谐波，只含有角频率为ωc及其附近的谐波，以及2ωc、3ωc等及其附近的谐波。 幅值最高影响最大的是角频率为ωc的谐波分量。

三相桥式PWM逆变电路

输出电压频谱图如下：

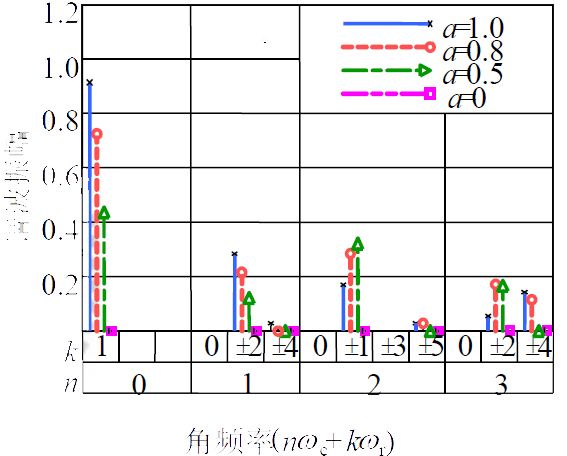
分析应用较多的公用载波信号时的情况，在其输出线电压 中，所包含的谐波角频率为

nωc±kωr

式中，n=1，3，5,...时，k=3（2m-1）±1，m=1，2,...;n=2，4，6,...时，k=6m+1，m=0，1,.../k=6m-1，m=1，2,...

不含有低次谐波，载波角频率ωc整数倍的角频率没有了，谐波中幅值较高的是ωc±2ωr和2ωc±ωr。

关于PWM逆变中谐波的几点小结：

①在实际电路中，由于采样时刻的误差以及为避免同一相上下桥臂直通而设置的死区的影响，谐波的分布情况 将更为复杂，谐波含量比理想条件下要多一些，甚至还
会出现少量的低次谐波。

②SPWM波形中所含的谐波主要是角频率为ωc、2ωc及其附近的谐波，一般情况下ωc>>ωr，是很容易滤除的。

③当调制信号波不是正弦波，而是其它波形时，其谐波由两部分组成，一部分是对信号波本身进行谐波分析所 得的结果，另一部分是由于信号波对载波的调制而产生
的谐波。

2提高直流电压利用率和减少开关次数

提高直流电压利用率、减少开关次数在PWM型逆变电路中是很重要的。

①直流电压利用率是指逆变电路所能输出的交流电压基波最大幅值U1m和直流电压Ud之比。

②提高直流电压利用率可以提高逆变器的输出能力。

③减少功率器件的开关次数可以降低开关损耗。

正弦波调制的三相PWM逆变电路的直流电压利用率很低。 在调制度a为最大值1时，输出相电压的基波幅值为Ud/2，输出线电压的基波幅值为(√3/2)Ud，即直流电压利用率仅为0.866。 实际电路工作时，考虑到功率器件的开通和关断都需要时间，如不采取其他措施，调制度不可能达到1，实际能得到的直流电压利用率比0.866还要低。

采用梯形波作为调制信号

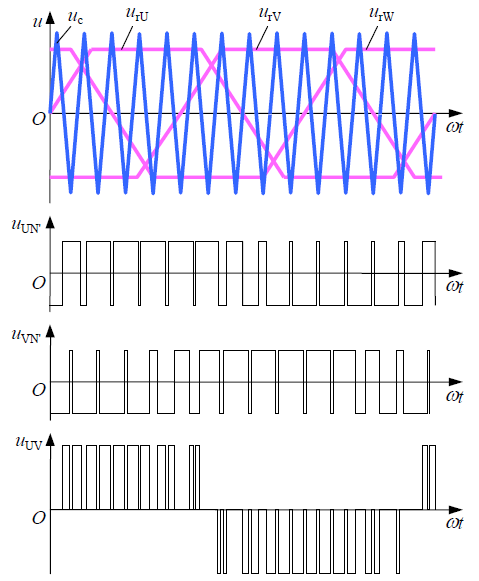
当梯形波幅值和三角波幅值相等时，梯形波所含的基波分量幅值已超过了三角波幅值，可以有效地提高直流电压利用率。 决定功率开关器件通断的方法和用正弦波作为调制信号波时完全相同; 对梯形波的形状用三角化率σ=Ut/Uto来描述，其中Ut为以横轴为底时梯形波的高，Uto为以横轴为底边把梯形两腰延长后相交所形成的三角形的高。

σ=0时梯形波变为矩形波，σ=1时梯形波变为三角波。

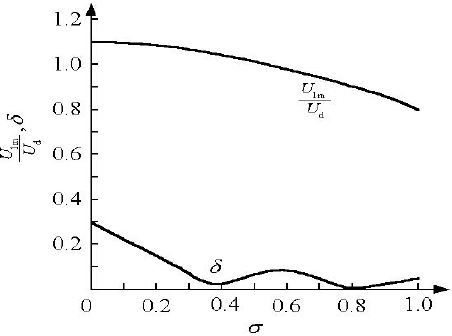
σ变化时的δ和直流电压利用率

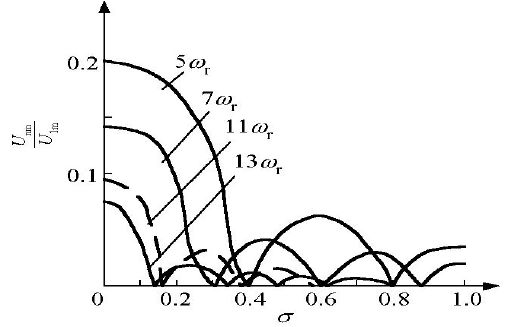
σ变化时的各次谐波含量

由于梯形波中含有低次谐波，调制后的PWM波仍含有同样的低次谐波，设由这些低次谐波(不包括由载波引起的谐波)产生的波形畸变率为б，则三角化率σ不同时，б和直流电压利用率U1m/Ud也不同。 σ=0.4时，谐波含量也较少，约为3.6%，直流电压利用率为1.03，综合效果较好。

用梯形波调制时，输出波形中含有5次、7次等低次谐波，这是梯形波调制的缺点，实际应用时，可以考虑将正弦波和梯形波结合使用。

线电压控制方式

目标是使输出的线电压波形中不含低次谐波，同时尽可能提高直流电压利用率，也应尽量减少功率器件的开关次数。

在相电压正弦波调制信号中叠加适当大小的3次谐波，使之成为鞍形波，
则经过PWM调制后逆变电路输出的相电压中也必然包含3次谐波，且三相的三次谐波相位相同，在合成线电压时，各相电压的3次谐波相互抵消，线电压为正弦波。

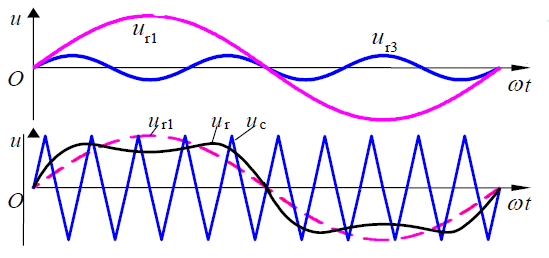
叠加3次谐波的调制信号

调制信号ur成为鞍形波，基波分量ur1的幅值更大，但ur的最大值不超过三角波载波最大值。 基波ur1正峰值附近恰为3次谐波ur3的负半波，两者相互抵消。

可以在正弦调制信号中叠加3次谐波外，还可以叠加其他3倍频于正弦波的信号，也可以再叠加直流分量，这些都不会影响线电压。