相位噪声与时间抖动有着什么关系？

相位噪声与时间抖动貌似毫不相干，但却是形影不离的，都是描述信号频率稳定性的参数，只是切入的角度不同。时间抖动的类型有很多，哪一种抖动是与相位噪声相对应的，彼此之间又有什么样的关系，下面将为您揭晓答案。

什么是相位噪声？什么是时间抖动？

您是否深究过相位噪声的定义？实际上，IEEE先后给过两种相位噪声的定义，最早的定义也是大家最熟知：距离载波一定频偏处，噪声功率谱密度与载波功率的比值即为相位噪声。

这种方法测试的相位噪声并不是纯相位噪声，同时还包含了调幅噪声(AM噪声)。为了准确表征相位噪声，IEEE后来又给了一版比较拗口的定义，这不是本文的重点，不再展开描述。 至于时间抖动，更多情况下是高速串行通信中会关注这个参数，主要是指信号边沿的波动情况。SONET(Synchronous Optical Network)规范中给出的时间抖动定义是：数字信号的边沿在时间上相对于理想位置的短期波动偏移量。从高速串行信号的角度讲，这个定义更多是指TIE(Time Interval Error)。

根据具体的成因，TIE又可以分为多种类型的抖动分量：随机抖动(RJ)、周期性抖动(PJ)、码型相干抖动(DDJ或ISI jitter)、占空比失真(DCD)等。其中，随机抖动是因随机噪声导致的信号边沿的波动，是与相位噪声相对应的抖动。因此，下面将着重介绍随机抖动与相位噪声的关系。

值得一提的是，相位噪声通常是针对于正弦波信号而言的，同时正弦波信号又是一种特殊的串行信号，因此，下面的内容都是以正弦波信号为例进行介绍。

相位噪声与时间抖动有着什么关系？

理想的正弦波信号用公式可以表示为

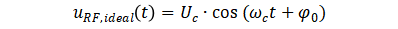
想象一下，理想正弦波信号的频谱就是非常纯净的单根谱线，没有任何边带。

而实际并不存在理想的正弦波信号，从频谱上看，实际的正弦波信号频谱都是具有左右对称的两个边带，为什么会这样呢？

这正是相位噪声和调幅噪声的缘故，相位噪声可以理解为宽带噪声对载波信号的相位调制，调幅噪声可以理解为宽带噪声对载波的幅度调制。回忆一下大学时期学习模拟调制的课程，AM/FM/ PM调制的频谱都是关于载波对称的。因此，正弦波信号的频谱具有对称的左右两个边带。

从相位调制的角度看，经宽带随机噪声u(t) 调制后，已调信号可以表示为

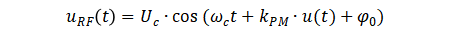
式中，kPM为调相比例系数，u(t) 为宽带随机信号，通常可以视为白噪声信号，相当于由无数个点频信号叠加而成。

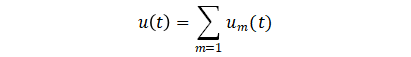
对于 u(t) 中包含的任意频点 ꞷm，对应的调制信号表达式为

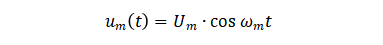
下面以频率为ꞷm的信号作为调制信号，从数学的角度推导单边带相位噪声与时间抖动的关系。 对射频载波调相后，已调信号的表达式为

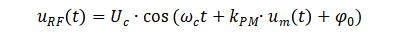
由调制信号引起的载波信号的瞬时相位定义为

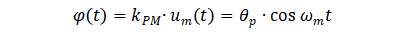
通常称θp为调相因子，表征了载波信号相位波动的最大偏移，单位为弧度rad.，其表达式为

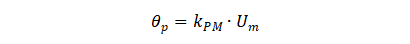
因此，已调信号又可以写为

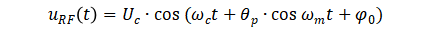
将上式展开为

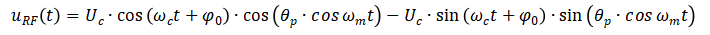
因宽带噪声幅度非常小，对载波信号进行相位调制造成的相位偏移也是非常小的，通常θp<<1，则存在如下近似关系： sin(θp·cos ꞷmt) ≈ θp·cos ꞷmt，cos(θp·cos ꞷmt) ≈ √1-( θp·cos ꞷmt)2→1 上式可进一步写为

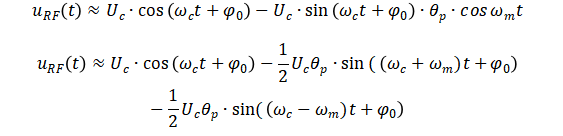
理论上，如果使用单频点信号作为调制信号对射频载波进行相位调制，已调信号可以展开为第一类贝塞尔函数，从展开式可以看出，频谱分量非常丰富，而且关于载波频率左右对称。而上面的公式表明，却只有载波、左右边带三个频率分量，这正是因为上面做了一些数学近似。

以右边带为例，其信号功率为

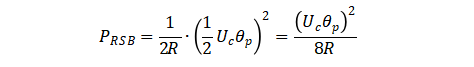
载波信号功率为

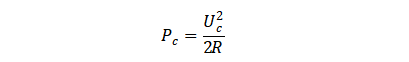
则在频偏 fm=ꞷm/2π 处的单边带相位噪声为

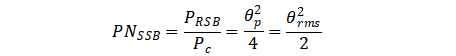
式中，θrms为载波信号相位波动的有效值。该公式具有普遍适用性，适用于任意频偏。

相位噪声表征了某一频偏处的单边带相对噪声功率谱密度，由上式可知，θ2rms表征了双边带相对噪声功率谱密度。

上面是以宽带随机噪声中的任意单频点信号作为调制信号为例，简要描述了相位噪声的形成，而宽带噪声包含无数个单频点信号，对载波进行相位调制后，那么从频谱上看，同样可以得到左右对称的两个边带，而且左右边带的频谱是连续的。

随机抖动与相位噪声有什么关系呢？

时间抖动就是指载波信号上升沿或者下降沿在时间轴上的短期波动，随机抖动是由于宽带噪声引起的边沿无规则随机波动，这与相位噪声是一一对应的，边沿的波动是各个频偏处相噪的综合体现。载波边沿的随机波动，存在一个波动范围，从概率密度上讲，基本服从高斯分布，通常采用标准差表征随机抖动，这也是随机抖动的有效值，也是通常要测试的参数。

时间抖动引起了相位的波动，只要确定了相位波动的量，那么也就确定了时间抖动。

将各个频偏处的相位噪声求和并进一步变换可得

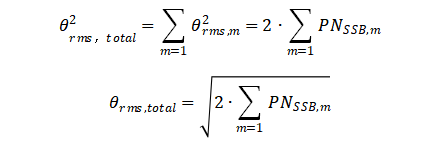
由于相位噪声的边带是连续的，因此，上式可以用积分表示

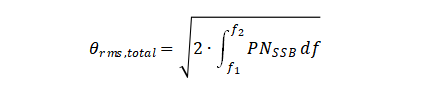
当然，测试设备是没有办法进行积分的，只能对离散的测试数据进行求和来模拟积分的效果。

θrms,total即为由总体的相位噪声引起的相位波动，结合载波频率并运用如下公式便可以计算出对应的时间抖动

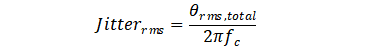
值得一提的是，上述公式中的相位噪声不是对数值，而是线性值！而且，根据相位噪声计算得到的抖动为随机抖动，换言之，随机抖动与相位噪声是一一对应的。

如果根据频谱仪或者相噪测试仪测得的相位噪声结果手动计算随机抖动，则需要注意：

由于仪表并不能测出所有频偏处的相位噪声，而是给出若干个均匀的离散频偏处的相噪，因此计算抖动的思路为：(1) 确定测试频偏离散点之间的频间距，可以从仪表导出的数据中明确；(2) 在频间距范围内，认为相噪是一个常数。故实际运算时的公式如下：

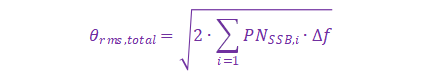
式中，∆f为频间距，单位为Hz。

如何测试时间抖动？

从目前看，关注时间抖动的信号主要分为两类：快沿信号和CW信号。前者通常是指在高速串行总线通信中的比特流信号及其时钟信号，这类信号普遍具有非常快的边沿，频谱分量较为丰富。后者主要是指诸如射频载波、晶振信号等单频点信号，这类信号频谱相对单一。

使用示波器是测试时间抖动最直接的方法，可以直接测试抖动，而不需要由相位噪声推导而来，对于上述两类信号都是适用的。尤其是对于快沿信号，不仅要测试各种抖动分量，还要测试幅度、边沿时间以及眼图等信号特征参数，必须要使用示波器进行测试。

对于CW信号，基本上只关注随机抖动，如果给出了抖动的指标要求，一定会给出对应的是哪个频偏范围。中高端示波器可以直接测试随机抖动，而且支持设定积分频偏范围，观测该频偏范围内的总随机抖动。但缺点是，示波器自身的抖动噪底往往较大，如果CW信号自身的随机抖动与示波器抖动噪底相当，那么就无法直接准确测试了。

如前所述，由相位噪声可以推导出随机抖动，那么就可以先测试相位噪声，然后再根据公式计算出随机抖动。通过配置自动相噪测试选件，中高端频谱仪测试相噪和抖动更加方便。而且单纯从随机抖动的测试能力而言，频谱仪自身的抖动噪底也好很多，如果超出了频谱仪的测试能力，还可以选择测试相噪的“专家级”设备——相噪测试仪，相噪测试能力更强。优点很明显，但缺点也很明显，这些频域设备只能测试频域相关参数，却无法进行时域相关测试！

无论是使用示波器直接测试随机抖动，还是使用频谱仪等设备先测试相噪、再计算随机抖动，整个测试都是非常简单、智能的。那么，应该如何选择呢？关键还是取决于仪表自身的测试能力和功能是否满足需求！

审核编辑：刘清