

简述游戏中常用的两种随机算法(下)
电子说
描述
先说结论,当你遇到第i个元素时,应该有1/i的概率选择该元素,1 - 1/i的概率保持原有的选择 。看代码容易理解这个思路:
/* 返回链表中一个随机节点的值 */
int getRandom(ListNode head) {
Random r = new Random();
int i = 0, res = 0;
ListNode p = head;
// while 循环遍历链表
while (p != null) {
i++;
// 生成一个 [0, i) 之间的整数
// 这个整数等于 0 的概率就是 1/i
if (0 == r.nextInt(i)) {
res = p.val;
}
p = p.next;
}
return res;
}
对于概率算法,代码往往都是很浅显的,但是这种问题的关键在于证明,你的算法为什么是对的?为什么每次以1/i的概率更新结果就可以保证结果是平均随机的?
我们来证明一下,假设总共有n个元素,我们要的随机性无非就是每个元素被选择的概率都是1/n对吧,那么对于第i个元素,它被选择的概率就是:
第i个元素被选择的概率是1/i,在第i+1次不被替换的概率是1 - 1/(i+1),在第i+2次不被替换的概率是1 - 1/(i+2),以此类推,相乘的结果是第i个元素最终被选中的概率,也就是1/n。因此,该算法的逻辑是正确的。
同理,如果要在单链表中随机选择k个数,只要在第i个元素处以k/i的概率选择该元素,以1 - k/i的概率保持原有选择即可 。代码如下:
/* 返回链表中 k 个随机节点的值 */
int[] getRandom(ListNode head, int k) {
Random r = new Random();
int[] res = new int[k];
ListNode p = head;
// 前 k 个元素先默认选上
for (int i = 0; i < k && p != null; i++) {
res[i] = p.val;
p = p.next;
}
int i = k;
// while 循环遍历链表
while (p != null) {
i++;
// 生成一个 [0, i) 之间的整数
int j = r.nextInt(i);
// 这个整数小于 k 的概率就是 k/i
if (j < k) {
res[j] = p.val;
}
p = p.next;
}
return res;
}
对于数学证明,和上面区别不大:
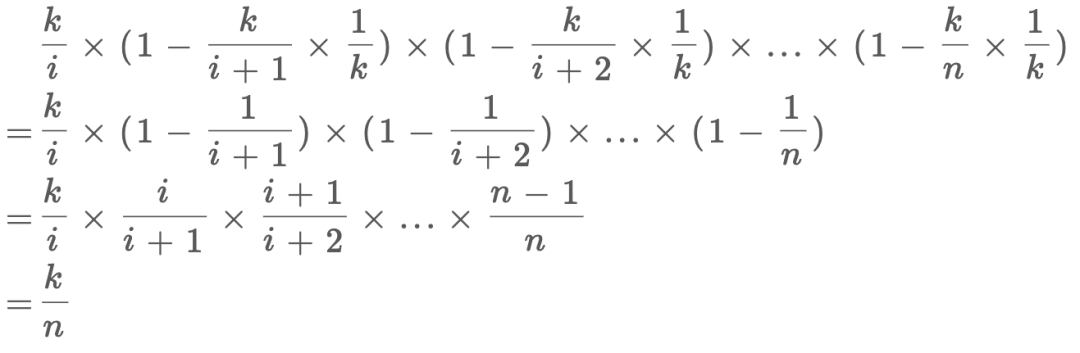
虽然每次更新选择的概率增大了k倍,但是选到具体第i个元素的概率还是要乘1/k,也就回到了上一个推导。
类似的,回到扫雷游戏的随机初始化问题,我们可以写一个这样的sample抽样函数:
// 在区间 [lo, hi) 中随机抽取 k 个数字
int[] sample(int lo, int hi, int k) {
Random r = new Random();
int[] res = new int[k];
// 前 k 个元素先默认选上
for (int i = 0; i < k; i++) {
res[i] = lo + i;
}
int i = k;
// while 循环遍历数字区间
while (i < hi - lo) {
i++;
// 生成一个 [0, i) 之间的整数
int j = r.nextInt(i);
// 这个整数小于 k 的概率就是 k/i
if (j < k) {
res[j] = lo + i - 1;
}
}
return res;
}
这个函数能够在一定的区间内随机选择k个数字,确保抽样结果是均匀随机的且只需要 O(N) 的时间复杂度。
蒙特卡洛验证法
上面讲到的洗牌算法和水塘抽样算法都属于随机概率算法,虽然从数学上推导上可以证明算法的思路是正确的,但如果你笔误写出 bug,就会导致概率上的不均等。更神奇的是,力扣的判题机制能够检测出这种概率错误。
那么最后我就来介绍一种方法检测随机算法的正确性:蒙特卡洛方法。我猜测力扣的判题系统也是利用这个方法来判断随机算法的正确性的。
记得高中有道数学题:往一个正方形里面随机打点,这个正方形里紧贴着一个圆,告诉你打点的总数和落在圆里的点的数量,让你计算圆周率。
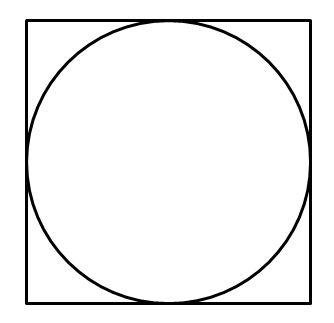
这其实就是利用了蒙特卡罗方法:当打的点足够多的时候,点的数量就可以近似代表图形的面积。结合面积公式,可以很容易通过正方形和圆中点的数量比值推出圆周率的。
当然,打的点越多,算出的圆周率越准确,充分体现了大力出奇迹的道理。
比如,我们可以这样检验水塘抽样算法sample函数的正确性:
public static void main(String[] args) {
// 在 [12, 22) 中随机选 3 个数
int lo = 12, hi = 22, k = 3;
// 记录每个元素被选中的次数
int[] count = new int[hi - lo];
// 重复 10 万次
int N = 1000000;
for (int i = 0; i < N; i++) {
int[] res = sample(lo, hi, k);
for (int elem : res) {
// 对随机选取的元素进行记录
count[elem - lo]++;
}
}
System.out.println(Arrays.toString(count));
}
这段代码的输出如下:
[300821, 299598, 299792, 299198, 299510, 300789, 300022, 300326, 299362, 300582]
当然你可以做更细致的检查,不过粗略看看,各个元素被选中的次数大致是相同的,这个算法实现的应该没啥问题。
对于洗牌算法中的shuffle函数也可以采取类似的验证方法,我们可以跟踪某一个元素x被打乱后的索引位置,如果x落在各个索引的次数基本相同,则说明算法正确,你可以自己尝试实现,我就不贴代码验证了。
拓展延伸
到这里,常见的随机算法就讲完了,简单总结下吧。
洗牌算法主要用于打乱数组,比如我们在 快速排序详解及运用中就用到了洗牌算法保证快速排序的效率。
水塘抽样算法的运用更加广泛,可以在序列中随机选择若干元素,且能保证每个元素被选中的概率均等。
对于这些随机概率算法,我们可以用蒙特卡洛方法检验其正确性。
最后留几个拓展题目:
1、本文开头讲到了将二维数组坐标(x, y)转化成一维数组索引的技巧,那么你是否有办法把三维坐标(x, y, z)转化成一维数组的索引呢?
2、如何对带有权重的样本进行加权随机抽取?比如给你一个数组w,每个元素w[i]代表权重,请你写一个算法,按照权重随机抽取索引。比如w = [1,99],算法抽到索引 0 的概率是 1%,抽到索引 1 的概率是 99%。
3、实现一个生成器类,构造函数传入一个很长的数组,请你实现randomGet方法,每次调用随机返回数组中的一个元素,多次调用不能重复返回相同索引的元素。要求不能对该数组进行任何形式的修改,且操作的时间复杂度是 O(1)
-
简述两种示波器测量眼图的差别2010-04-21 4090
-
两种典型的ADRC算法介绍2021-09-07 3508
-
智能插座常用的两种通信协议是什么?2021-09-26 1494
-
网络中常用的队列管理方法比较2009-05-25 575
-
基于游戏中NPC路径规划的混合算法2017-11-14 1063
-
帕塞瓦定理的两种常见形式2018-04-02 10373
-
Wincc如何与PLC进行通讯两种常用的方式介绍2019-02-17 31529
-
单片机常用的两种延时控制方式2020-07-17 6632
-
常用的hdl语言有哪两种2020-08-25 9830
-
说透游戏中常用的两种随机算法2022-11-09 1639
-
详解PMSM中常用的两种坐标变换2023-01-19 3988
-
简述游戏中常用的两种随机算法(上)2023-04-12 1307
-
基于Python实现随机森林算法2023-09-21 2306
-
PCBA加工中常见的两种焊接方式详解2024-06-14 1350
-
真随机数和伪随机数的区别2025-08-27 2060
全部0条评论

快来发表一下你的评论吧 !

