

算法时空复杂度分析实用指南2
电子说
描述
计算平均时间复杂度最常用的方法叫做「聚合分析」,思路如下 :
给你一个空的MonotonicQueue,然后请你执行N个push, pop组成的操作序列,请问这N个操作所需的总时间复杂度是多少?
因为这N个操作最多就是让O(N)个元素入队再出队,每个元素只会入队和出队一次,所以这N个操作的总时间复杂度是O(N)。
那么平均下来,一次操作的时间复杂度就是O(N)/N = O(1),也就是说push和pop方法的平均时间复杂度都是O(1)。
类似的,想想之前说的数据结构扩容的场景,也许N次操作中的某一次操作恰好触发了扩容,导致时间复杂度提高,但总的时间复杂度依然保持在O(N),所以均摊到每一次操作上,其平均时间复杂度依然是O(1)。
递归算法分析
对很多人来说,递归算法的时间复杂度是比较难分析的。但如果你有 框架思维,明白所有递归算法的本质是树的遍历,那么分析起来应该没什么难度。
计算算法的时间复杂度,无非就是看这个算法做了些啥事儿,花了多少时间。而递归算法做的事情就是遍历一棵递归树,在树上的每个节点所做一些事情罢了。
所以:
递归算法的时间复杂度 = 递归的次数 x 函数本身的时间复杂度
递归算法的空间复杂度 = 递归堆栈的深度 + 算法申请的存储空间
或者再说得直观一点:
递归算法的时间复杂度 = 递归树的节点个数 x 每个节点的时间复杂度
递归算法的空间复杂度 = 递归树的高度 + 算法申请的存储空间
函数递归的原理是操作系统维护的函数堆栈,所以递归栈的空间消耗也需要算在空间复杂度之内,这一点不要忘了。
首先说一下动态规划算法 ,还是拿前文 动态规划核心框架中讲到的凑零钱问题举例,它的暴力递归解法主体如下:
int dp(int[] coins, int amount) {
// base case
if (amount == 0) return 0;
if (amount < 0) return -1;
int res = Integer.MAX_VALUE;
// 时间 O(K)
for (int coin : coins) {
int subProblem = dp(coins, amount - coin);
if (subProblem == -1) continue;
res = Math.min(res, subProblem + 1);
}
return res == Integer.MAX_VALUE ? -1 : res;
}
当amount = 11, coins = [1,2,5]时,该算法的递归树就长这样:
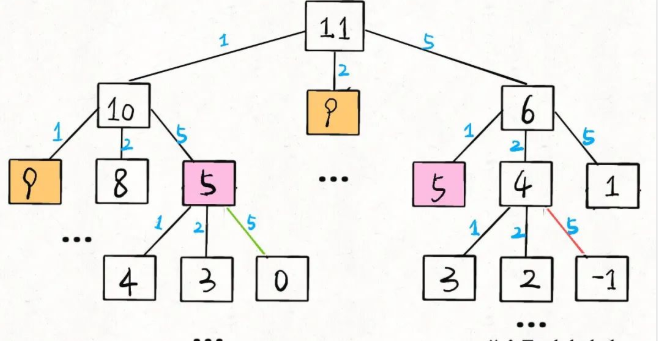
刚才说了这棵树上的节点个数为O(K^N),那么每个节点消耗的时间复杂度是多少呢?其实就是这个dp函数本身的复杂度。
你看dp函数里面有个 for 循环遍历长度为K的coins列表,所以函数本身的复杂度为O(K),故该算法总的时间复杂度为:
O(K^N) * O(K) = O(K^(N+1))
当然,之前也说了,这个复杂度只是一个粗略的上界,并不准确,真实的效率肯定会高一些。
这个算法的空间复杂度很容易分析:
dp函数本身没有申请数组之类的,所以算法申请的存储空间为O(1);而dp函数的堆栈深度为递归树的高度O(N),所以这个算法的空间复杂度为O(N)。
暴力递归解法的分析结束,但这个解法存在重叠子问题,通过备忘录消除重叠子问题的冗余计算之后,相当于在原来的递归树上进行剪枝:
// 备忘录,空间 O(N)
memo = new int[N];
Arrays.fill(memo, -666);
int dp(int[] coins, int amount) {
if (amount == 0) return 0;
if (amount < 0) return -1;
// 查备忘录,防止重复计算
if (memo[amount] != -666)
return memo[amount];
int res = Integer.MAX_VALUE;
// 时间 O(K)
for (int coin : coins) {
int subProblem = dp(coins, amount - coin);
if (subProblem == -1) continue;
res = Math.min(res, subProblem + 1);
}
// 把计算结果存入备忘录
memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
return memo[amount];
}
通过备忘录剪掉了大量节点之后,虽然函数本身的时间复杂度依然是O(K),但大部分递归在函数开头就立即返回了,根本不会执行到 for 循环那里,所以可以认为递归函数执行的次数(递归树上的节点)减少了,从而时间复杂度下降。
剪枝之后还剩多少节点呢?根据备忘录剪枝的原理,相同「状态」不会被重复计算,所以剪枝之后剩下的节点数就是「状态」的数量,即memo的大小N。
所以,对于带备忘录的动态规划算法的时间复杂度,以下几种理解方式都是等价的:
递归的次数 x 函数本身的时间复杂度
= 递归树节点个数 x 每个节点的时间复杂度
= 状态个数 x 计算每个状态的时间复杂度
= 子问题个数 x 解决每个子问题的时间复杂度
= O(N) * O(K)
= O(NK)
像「状态」「子问题」属于动态规划类型问题特有的词汇,但时间复杂度本质上还是递归次数 x 函数本身复杂度,换汤不换药罢了。反正你爱怎么说怎么说吧,别把自己绕进去就行。
备忘录优化解法的空间复杂度也不难分析:
dp函数的堆栈深度为「状态」的个数,依然是O(N),而算法申请了一个大小为O(N)的备忘录memo数组,所以总的空间复杂度为O(N) + O(N) = O(N)。
虽然用 Big O 表示法来看,优化前后的空间复杂度相同,不过显然优化解法消耗的空间要更多,所以用备忘录进行剪枝也被称为「用空间换时间」。
如果你把自顶向下带备忘录的解法进一步改写成自底向上的迭代解法:
int coinChange(int[] coins, int amount) {
// 空间 O(N)
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
// 时间 O(KN)
for (int i = 0; i < dp.length; i++) {
for (int coin : coins) {
if (i - coin < 0) continue;
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
该解法的时间复杂度不变,但已经不存在递归,所以空间复杂度中不需要考虑堆栈的深度,只需考虑dp数组的存储空间,虽然用 Big O 表示法来看,该算法的空间复杂度依然是O(N),但该算法的实际空间消耗是更小的,所以自底向上迭代的动态规划是各方面性能最好的。
接下来说一下回溯算法 ,需要你看过前文 回溯算法秒杀排列组合问题的 9 种变体,下面我会以标准的全排列问题和子集问题的解法为例,分析一下其时间复杂度。
先看标准全排列问题 (元素无重不可复选)的核心函数backtrack:
// 回溯算法计算全排列
void backtrack(int[] nums) {
// 到达叶子节点,收集路径值,时间 O(N)
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
// 非叶子节点,遍历所有子节点,时间 O(N)
for (int i = 0; i < nums.length; i++) {
if (used[i]) {
// 剪枝逻辑
continue;
}
// 做选择
used[i] = true;
track.addLast(nums[i]);
backtrack(nums);
// 取消选择
track.removeLast();
used[i] = false;
}
}
当nums = [1,2,3]时,backtrack其实在遍历这棵递归树:

假设输入的nums数组长度为N,那么这个backtrack函数递归了多少次?backtrack函数本身的复杂度是多少?
先看看backtrack函数本身的时间复杂度,即树中每个节点的复杂度。
对于非叶子节点,会执行 for 循环,复杂度为O(N);对于叶子节点,不会执行循环,但将track中的值拷贝到res列表中也需要O(N)的时间, 所以backtrack函数本身的时间复杂度为O(N) 。
PS:函数本身(每个节点)的时间复杂度并不是树枝的条数。看代码,每个节点都会执行整个 for 循环,所以每个节点的复杂度都是
O(N)。
再来看看backtrack函数递归了多少次,即这个排列树上有多少个节点。
第 0 层(根节点)有P(N, 0) = 1个节点。
第 1 层有P(N, 1) = N个节点。
第 2 层有P(N, 2) = N x (N - 1)个节点。
第 3 层有P(N, 3) = N x (N - 1) x (N - 2)个节点。
以此类推,其中P就是我们高中学过的排列数函数。
全排列的回溯树高度为N,所以节点总数为:
P(N, 0) + P(N, 1) + P(N, 2) + ... + P(N, N)
这一堆排列数累加不好算,粗略估计一下上界吧,把它们全都扩大成P(N, N) = N!, 那么节点总数的上界就是O(N*N!) 。
现在就可以得出算法的总时间复杂度:
递归的次数 x 函数本身的时间复杂度
= 递归树节点个数 x 每个节点的时间复杂度
= O(N*N!) * O(N)
= O(N^2 * N!)
当然,由于计算节点总数的时候我们为了方便计算把累加项扩大了很多,所以这个结果肯定也是偏大的,不过用来描述复杂度的上界还是可以接受的。
分析下该算法的空间复杂度:
backtrack函数的递归深度为递归树的高度O(N),而算法需要存储所有全排列的结果,即需要申请的空间为O(N*N!)。 所以总的空间复杂度为O(N*N!) 。
最后看下标准子集问题 (元素无重不可复选)的核心函数backtrack:
// 回溯算法计算所有子集(幂集)
void backtrack(int[] nums, int start) {
// 每个节点的值都是一个子集,O(N)
res.add(new LinkedList<>(track));
// 遍历子节点,O(N)
for (int i = start; i < nums.length; i++) {
// 做选择
track.addLast(nums[i]);
backtrack(nums, i + 1);
// 撤销选择
track.removeLast();
}
}
当nums = [1,2,3]时,backtrack其实在遍历这棵递归树:

假设输入的nums数组长度为N,那么这个backtrack函数递归了多少次?backtrack函数本身的复杂度是多少?
先看看backtrack函数本身的时间复杂度,即树中每个节点的复杂度。
backtrack函数在前序位置都会将track列表拷贝到res中,消耗O(N)的时间,且会执行一个 for 循环,也消耗O(N)的时间, 所以backtrack函数本身的时间复杂度为O(N) 。
再来看看backtrack函数递归了多少次,即这个排列树上有多少个节点。
那就直接看图一层一层数呗:
第 0 层(根节点)有C(N, 0) = 1个节点。
第 1 层有C(N, 1) = N个节点。
第 2 层有C(N, 2)个节点。
第 3 层有C(N, 3)个节点。
以此类推,其中C就是我们高中学过的组合数函数。
由于这棵组合树的高度为N,组合数求和公式是高中学过的, 所以总的节点数为2^N :
C(N, 0) + C(N, 1) + C(N, 2) + ... + C(N, N) = 2^N
就算你忘记了组合数求和公式,其实也可以推导出来节点总数:因为N个元素的所有子集(幂集)数量为2^N,而这棵树的每个节点代表一个子集,所以树的节点总数也为2^N。
那么,现在就可以得出算法的总复杂度:
递归的次数 x 函数本身的时间复杂度
= 递归树节点个数 x 每个节点的时间复杂度
= O(2^N) * O(N)
= O(N*2^N)
分析下该算法的空间复杂度:
backtrack函数的递归深度为递归树的高度O(N),而算法需要存储所有子集的结果,粗略估算下需要申请的空间为O(N*2^N), 所以总的空间复杂度为O(N*2^N) 。
到这里,标准排列/子集问题的时间复杂度就分析完了,前文回溯算法秒杀排列组合问题的 9 种变体中的其他问题变形都可以按照类似的逻辑分析,这些就留给你自己分析吧。
最后总结
本文篇幅较大,我简单总结下重点:
1、Big O 标记代表一个函数的集合,用它表示时空复杂度时代表一个上界,所以如果你和别人算的复杂度不一样,可能你们都是对的,只是精确度不同罢了。
2、时间复杂度的分析不难,关键是你要透彻理解算法到底干了什么事。非递归算法中嵌套循环的复杂度依然可能是线性的;数据结构 API 需要用平均时间复杂度衡量性能;递归算法本质是遍历递归树,时间复杂度取决于递归树中节点的个数(递归次数)和每个节点的复杂度(递归函数本身的复杂度)。
好了,能看到这里,真得给你鼓掌。需要说明的是,本文给出的一些复杂度都是比较粗略的估算,上界都不是很「紧」,如果你不满足于粗略的估算,想计算更「紧」更精确的上界,就需要比较好的数学功底了。不过从面试笔试的角度来说,掌握这些基本分析技术已经足够应对了。
- 相关推荐
- 热点推荐
-
时间复杂度为 O(n^2) 的排序算法2024-10-19 2066
-
如何计算时间复杂度2023-10-13 4675
-
算法时空复杂度分析实用指南(上)2023-04-19 1467
-
算法时空复杂度分析实用指南12023-04-12 941
-
常见机器学习算法的计算复杂度2022-10-02 1109
-
算法之空间复杂度2022-08-31 2249
-
如何求递归算法的时间复杂度2022-07-13 2774
-
各种排序算法的时间空间复杂度、稳定性2021-12-21 1152
-
时间复杂度是指什么2021-07-22 1765
-
图像复杂度对信息隐藏性能影响分析2017-11-14 996
-
基于复杂度分析的改进A_算法飞行器航迹规划_丛林虎2017-03-17 876
-
LDPC码低复杂度译码算法研究2012-03-31 1104
-
基于纹理复杂度的快速帧内预测算法2010-05-06 3646
全部0条评论

快来发表一下你的评论吧 !

