

决策规划系列:运动规划常用算法
描述
有了全局路径参考信息,有了局部环境信息了,有了行为决策模块输入的决策信息,下一步自然而然的就要进行运动规划,从而生成一条局部的更加具体的行驶轨迹,并且这条轨迹要满足安全性和舒适性要求。
考虑到车辆是一个具有巨大惯性的铁疙瘩且没有瞬间移动的功能,如果仅考虑瞬时状态的行驶轨迹,不规划出未来一段时间有前瞻性的行驶轨迹,那么很容易造成一段时间后无解。因此,运动规划生成的轨迹是一种由二维空间和一维时间组成的三维空间中的曲线,是一种偏实时的路径规划。
运动规划的第一步往往采用随机采样算法,即走一步看一步,不断更新行驶轨迹。代表算法是基于采样的方法:PRM、RRT、Lattice。这类算法通过随机采样的方式在地图上生成子节点,并与父节点相连,若连线与障碍物无碰撞风险,则扩展该子节点。重复上述步骤,不断扩展样本点,直到生成一条连接起点到终点的路径。
PRM
概率路标法 (Probabilistic Road Maps, PRM),是一种经典的采样方法,由Lydia E.等人在1996年提出。PRM主要包含三个阶段,一是采样阶段,二是碰撞检测阶段,三是搜索阶段。
图25为已知起点A和终点B的地图空间,黑色空间代表障碍物,白色空间代表可通行区域。在采样阶段中,PRM首先在地图空间进行均匀的随即采样,也就是对地图进行稀疏采样,目的是将大地图简化为较少的采样点。
在碰撞检测阶段,剔除落在障碍物上的采样点,并将剩下的点与其一定距离范围内的点相连,同时删除穿越障碍物的连线,从而构成一张无向图。
在搜索阶段,利用全局路径规划算法章节介绍的搜索算法(Dijkstra、A*等)在无向图中进行搜索,从而找出一条起点A到终点B之间的可行路径。
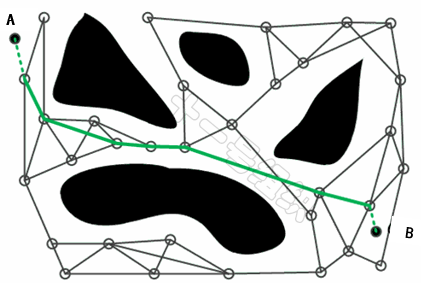
图27 PRM工作原理示意图(来源:https://mp.weixin.qq.com/s/WGOUf7g0C4Od4X9rnCfqxA)
算法步骤可以总结为:
(1)构造无向图G =(V,E),其中V代表随机采样的点集,E代表两采样点之间所有可能的无碰撞路径,G初始状态为空。
(2)随机撒点,并选取一个无碰撞的点c(i)加入到V中。
(3)定义距离r,如果c(i)与V中某些点的距离小于r,则将V中这些点定义为c(i)的邻域点。
(4)将c(i)与其邻域点相连,生成连线t,并检测连线t是否与障碍物发生碰撞,如果无碰撞,则将t加入E中。
(5)重复步骤2-4,直到所有采样点(满足采样数量要求)均已完成上述步骤。
(5)采用图搜索算法对无向图G进行搜索,如果能找到起始点A到终点B的路线,说明存在可行的行驶轨迹。
PRM算法相比基于搜索的算法,简化了环境、提高了效率。但是在有狭窄通道场景中,很难采样出可行路径,效率会大幅降低。
RRT
快速探索随机树(Rapidly Exploring Random Trees,RRT),是Steven M. LaValle和James J. Kuffner Jr.在1998年提出的一种基于随机生长树思想实现对非凸高维空间快速搜索的算法。与PRM相同的是两者都是基于随机采样的算法,不同的是PRM最终生成的是一个无向图,而RRT生成的是一个随机树。RRT的最显著特征就是具备空间探索的能力,即从一点向外探索拓展的特征。
RRT分单树和双树两种类型,单树RRT将规起点作为随机树的根节点,通过随机采样、碰撞检测的方式为随机树增加叶子节点,最终生成一颗随机树。而双树RRT则拥有两颗随机树,分别以起点和终点为根节点,以同样的方式进行向外的探索,直到两颗随机树相遇,从而达到提高规划效率的目的。
下面以图28所示的地图空间为例介绍单树RRT算法的实现过程。在此地图空间中,我们只知道起点A和终点B以及障碍物的位置(黑色的框)。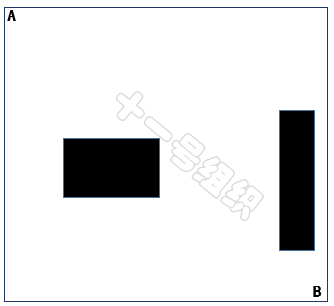
图28 RRT算法举例的地图空间
对于单树RRT算法,我们将起点A设置为随机树的根,并生成一个随机采样点,如图27所示,随机采样点有下面这几种情况。
(1)随机采样点1落在自由区域中,但是根节点A和随机采样点1之间的连线存在障碍物,无法通过碰撞检测,采样点1会被舍弃,重新再生成随机采样点。
(2)随机采样点2落在障碍物的位置,采样点2也会被舍弃,重新再生成随机采样点。
(3)随机采样点3落在自由区域,且与根节点A之间的连线不存在障碍物,但是超过根节点的步长限制。但此时这个节点不会被简单的舍弃点,而是会沿着根节点和随机采样点3的连线,找出符合步长限制的中间点,将这个中间点作为新的采样点,也就是图29中的4。
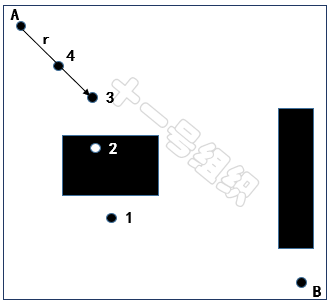
图29 不同随机采样点举例
接着我们继续生成新的随机采样点,如果新的随机采样点位于自由区域,那么我们就可以遍历随机树中已有的全部节点,找出距离新的随机采样点最近的节点,同时求出两者之间的距离,如果满足步长限制的话,我们将接着对这两个节点进行碰撞检测,如果不满足步长限制的话,我们需要沿着新的随机采样点和最近的节点的连线方向,找出一个符合步长限制的中间点,用来替代新的随机采样点。最后如果新的随机采样点和最近的节点通过了碰撞检测,就意味着二者之间存在边,我们便可以将新的随机采样点添加进随机树中,并将最近的点设置为新的随机采样点的父节点。
重复上述过程,直到新的随机采样点在终点的步长限制范围内,且满足碰撞检测。则将新的随机采样点设为终点B的父节点,并将终点加入随机树,从而完成迭代,生成如图30所示的完整随机树。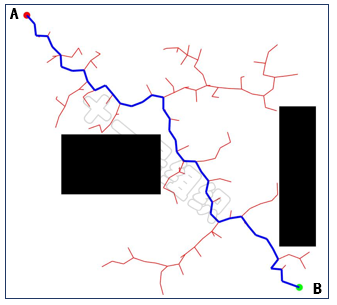
图30 随机树结算结果示例
相比PRM,RRT无需搜索步骤、效率更高。通过增量式扩展的方式,找到路径后就立即结束,搜索终点的目的性更强。但是RRT作为一种纯粹的随机搜索算法,对环境类型不敏感,当地图空间中存在狭窄通道时,因被采样的概率低,导致算法的收敛速度慢,效率会大幅下降,有时候甚至难以在有狭窄通道的环境找到路径。
图31展示了 RRT应对存在狭窄通道地图空间时的两种表现,一种是RRT很快就找到了出路,一种是一直被困在障碍物里面。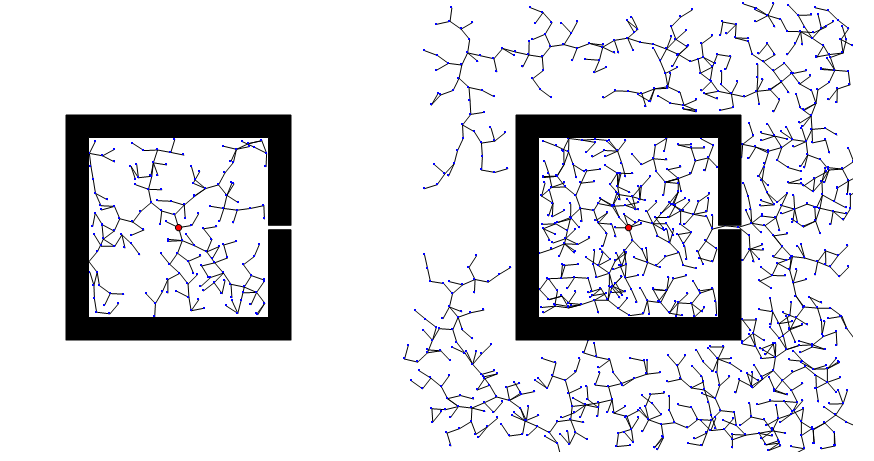
图31 RRT面对狭窄通道时的表现
围绕如何更好的“进行随机采样”、“定义最近的点”以及“进行树的扩展”等方面,诞生了多种改进型的算法,包括双树RRT-Connect(双树)、lazy-RRT, RRT-Extend等。
PRM和RRT都是一个概率完备但非最优的路径规划算法,也就是只要起点和终点之间存在有效的路径,那么只要规划的时间足够长,采样点足够多,必然可以找到有效的路径。但是这个解无法保证是最优的。
采用PRM和RRT等随机采样算法生成的行驶轨迹,大多是一条条线段,线段之间的曲率也不不连续,这样的行驶轨迹是不能保证舒适性的,所以还需要进一步进行曲线平滑、角度平滑处理。代表算法是基于曲线插值的方法:RS曲线、Dubins曲线、多项式曲线、贝塞尔曲线和样条曲线等。
所有基于曲线插值方法要解决的问题就是:在图32上的若干点中,求出一条光滑曲线尽可能逼近所有点。下文以多项式曲线和贝塞尔曲线为例,介绍曲线插值算法的示例。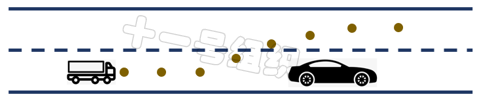
图32 曲线插值方法要解决的问题描述
多项式曲线
找到一条曲线拟合所有的点,最容易想到的方法就是多项式曲线。常用的有三阶多项式曲线、五阶多项式曲线和七阶多项式曲线。理论上只要多项式的阶数足够高,就可以拟合各种曲线。但从满足需求和工程实现的角度,阶数越低越好。
车辆在运动规划中,舒适度是一个非常重要的指标,在物理中衡量舒适性的物理量为跃度(Jerk),它是加速度的导数。Jerk的绝对值越小意味着加速度的变化越平缓,加速度的变化越平缓意味着越舒适。而五次多项式曲线则被证明是在运动规划中可以使Jerk比较小的多项式曲线。
以图30所示换道场景为例,已知Frenet坐标系下换道起点和终点的六个参数s0、v0、a0、st、vt、at,采用横纵向解耦分别进行运动规划的方法,可得横向位置x(t)和纵向位置y(t)关于时间t的五次多项式表达式。
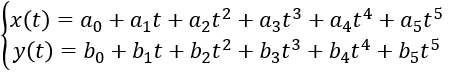
五次多项式中存在六个未知量,将起点和终点已知的六个参数代入便可这个六个未知量。然后根据时间t进行合并即可得到横纵向联合控制的曲线,即最终运动规划的曲线。
贝塞尔曲线
对于比较少的点来说,采用多项式曲线非常合理。但是当点比较多时,为了逼近所有点,就不得不增加多项式的次数,而由此带来的负面影响就是曲线震荡。退一步讲,即使震荡能够被消除,获得的曲线由于存在非常多的起伏,也不够光顺。而贝塞尔曲线的出现,正好解决了上述问题。
1959年,法国数学家保尔·德·卡斯特里使用独家配方求出贝塞尔曲线。1962年,法国雷诺汽车公司工程师皮埃尔·贝塞尔将自己在汽车造型设计的一些心得归纳总结,并广泛发表。贝塞尔在造型设计的心得可简单总结为:先用折线段勾画出汽车的外形大致轮廓,再用光滑的参数曲线去逼近这个折线多边形。
绘制贝塞尔曲线之前,我们需要知道起点和终点的参数,然后再提供任意数量的控制点的参数。如果控制点的数量为0,则为一阶贝塞尔曲线,如果控制点的数量为1,则为二阶贝塞尔曲线,如果控制点的数量为2,则为三阶贝塞尔曲线,依次类推。不论是起点、终点还是控制点,它们均代表坐标系下的一个向量。
下面我们以经典的二阶贝塞尔曲线为例,介绍其绘制方法。如图33所示,P0和P2为已知的参数的起点和终点,P1为已知参数的控制点。首先我们按照起点、控制点、终点的顺序依次连接,生成两条直线。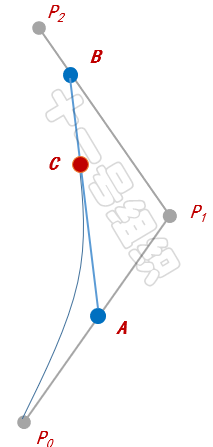
图33 二阶贝塞尔曲线示例
接着我们以每条直线的起点开始,向各自的终点按比例t取点,如图中的A和B。随后我们将A和B相连得到一条直线,也按相同的比例t取点,便可得到C点,这也是二阶贝塞尔曲线在比例为t时会经过的点。比列t满足如下的公式。
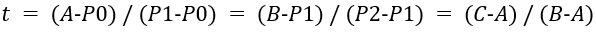
当我们比例t一点点变大(从0到1),就得到起点到终点的所有贝塞尔点,所有点相连便绘制出完整的二阶贝塞尔曲线C(t),用公式表达为。
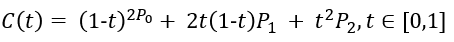
由二阶贝塞尔曲线拓展到N阶贝塞尔曲线,可得数学表达式如下。
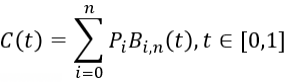
审核编辑:刘清
-
运动控制速度规划2015-09-04 4281
-
动态规划算法。2017-08-30 3130
-
LCS的动态规划算法2020-05-25 1200
-
飞行场地改造规划决策研究2010-08-06 780
-
算法大全_目标规划2016-01-14 512
-
一种用于内层规划的改进粒子群算法2017-12-19 823
-
配电网规划决策中的可计算性问题研究2018-03-10 979
-
Lattice Planner规划算法2018-09-05 11106
-
自动驾驶中基于图搜索的常用路径规划算法介绍2021-04-25 4164
-
强化学习与智能驾驶决策规划2023-02-08 2856
-
决策规划:行为决策常用算法2023-04-12 1771
-
自动驾驶决策规划模块算法介绍2023-06-01 531
-
自动驾驶决策规划算法第一章笔记2023-06-02 496
-
机器人技术中常用的路径规划算法的开源库2023-10-21 2274
-
全局路径规划RRT算法原理2023-11-24 1994
全部0条评论

快来发表一下你的评论吧 !

