嵌入式开发的一元线性回归算法介绍

   线性回归是最经典的最小二乘法、卡尔曼、维纳滤波器的基础，也是我在研究生阶段接触的第一个算法，第一次使用也是给导师做项目的时候用到的，工作之后发现这些算法在工程中无处不在，但是不幸的是很多朋友不会用这些数学算法，只会用滑动均值滤波、平均值滤波、低通、高通、带通、陷波这些简单的算法，这些算法虽然简单，但是它的作用确实没有最小二乘、卡尔曼滤波这些算法的效果好。前提是要正确运用这些算法，否则用了还不如不用。

其实回归算法是相对分类算法而言的，与我们想要预测的目标变量y的值类型有关。如果目标变量y是分类型变量，如预测用户的性别（男、女），预测月季花的颜色（红、白、黄……），预测是否患有肺癌（是、否），那我们就需要用分类算法去拟合训练数据并做出预测，学术上一般用SVM(支持向量机)、粒子群算法、神经网络算法等。但是在嵌入式开发尤其是单片机开发过程中，这些复杂算法因其复杂程度和运算量的关系，无法得到工程化应用，一般则用计算量较小更容易实现的卡尔曼或最小二乘法，然而一元线性回归则是最简单、理解起来最容易接受，也是应用最广泛的算法，当然也是现在比较火热的机器学习行业的入门算法。

      一元线性回归

一元线性回归顾名思义就是一个自变量（可以是ADC采集到的电压值、DS18B20采集到的温度值、也可以是光敏传感器采集的光照强度值）。下面我们以工作中最常见的电压采集为例，用一元线性回归的方法来预测我们的电压采集的线性方程，以我们物联网开发板的电压采集系统为例：

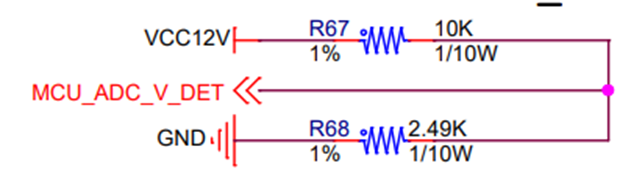
图1 输入电压12VADC电压采集电路

因为单片机可以采集的电压范围是0-3.3V（基本上采集满量程电压百分之六十是最准确的，往往硬件工程师在设计电路的时候也是这么考虑的），大家可以看到硬件电路采用分压电阻，将12V的电压分成1/11，将这个值送给单片机ADC，单片机采集到这个电压值，乘以11就是我们采集的电压值，这个我们很容易能够理解，因为输入电压基本上在12V上位微笑波动的数值，很容易我们能够反向回推。现实中我们也可以这么做，当然前提是我们要求采集的精度不高。但是在工控领域或者要求精度较高的测控领域，我们就要用到线性回归的的方法了。

假设电压输入范围是4-12V，因为ADC模块采集会有各种各样的误差（积分误差、微分误差、零漂、电路中电阻的精度误差）导致我们采集到的电压值有一定的误差，此时要很好地解决这个问题，我们就可以用最小二乘法来预测线性方程（用到的就是一元线性回归）。当然假设我们的系统是线性系统，这个要我们硬件设计的小伙伴尽量从硬件角度多考虑（电路阻抗匹配的设计、PCB的走线、ADC参考电压等方面去考虑），保证系统最大化接近线性就可以，系统不可能完全线性的。硬件偏差太大，软件也是有心杀贼无力回天了，从这个角度可以说软件是辅助硬件，加上算法是最大化辅助硬件。

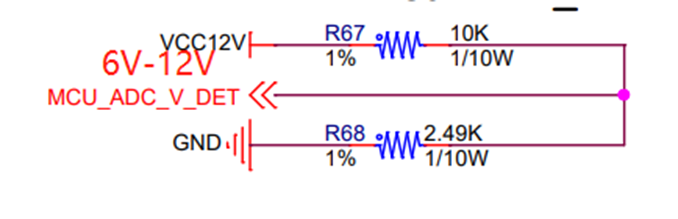
图2输入电压6V-12VADC电压采集电路

假设线性方程（1）所示：

y=β0+β1*x        （1）

这就是我们是我们平常所说的正比例函数。x是ADC采集到的电压值，Y是电源输入的电压值（6V-12V）β0、β1就是线性回归系数，也是我们用数学方法要预测的系数。

当我们只用一个x来预测y，就是一元线性回归，也就是在找一个直线来拟合数据。比如，我采集到的一组数据画出来的散点图，y代表输入电压，x是单片机ADC模块采集的值，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。

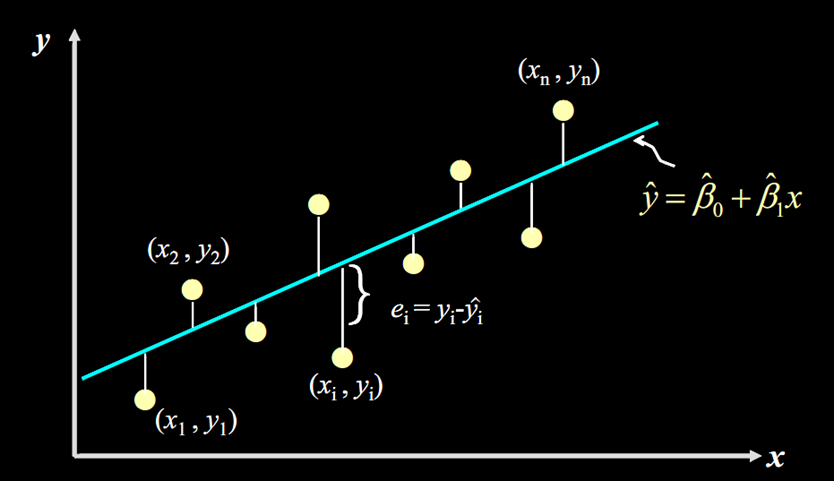
图3 线性回归拟合图

这里我们得到的拟合方程是：y =β^0+β^1*X。计算 图3输入电压（黄色的离散点）与用拟合函数（绿色线）计算出来电压之间的误差ei（ei=yi-y^i）的值，再将其平方（为了消除负号），对于我们数据中的每个点如此计算一遍，再将所有的 e

相加，就能量化出拟合的直线和实际之间的误差。

用公式表示就是：

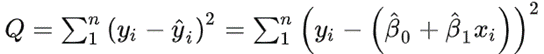
（2）

这个公式是残差平方和。也就是我们对“直线”的评价标准。这个函数的值越小，说明直线越能拟合我们的数据。

最小二乘估计

我们知道了直线拟合的评价标准，接下来我们目的是怎么用这个标准来预测β^0和β^1这两个系数的值。

公式（2）是一个二次方程，我们知道一元二次方程差不多长下图这样：

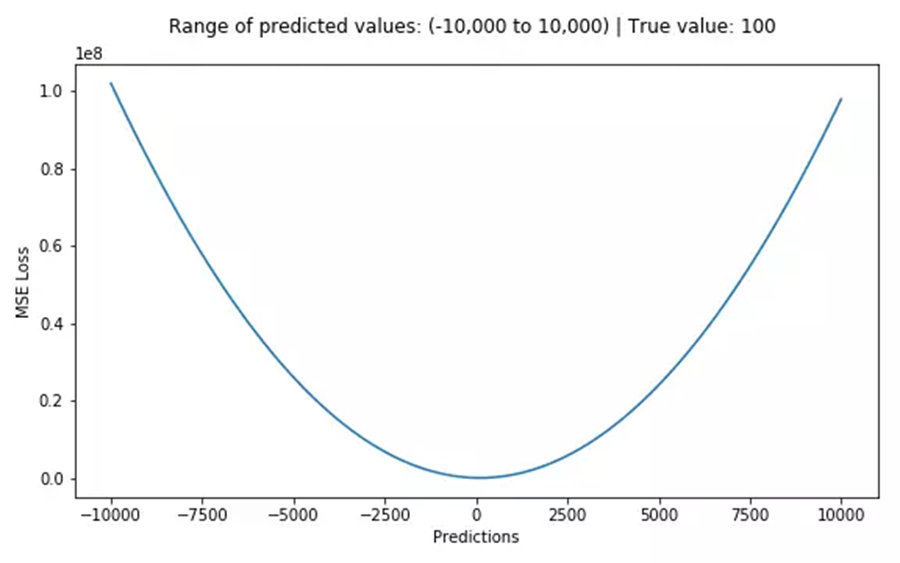
上面公式中β^0 和 β^1 未知，有两个未知参数的二次方程，这个方程开口向上，那么倒数为0就是图的极点，就是所说的残差和最小，满足了我们的评价标准。还记得微积分知识的话，就知道导数为0时，Q取最小值，因此我们分别对β^0和β^1求偏导并令其为0：

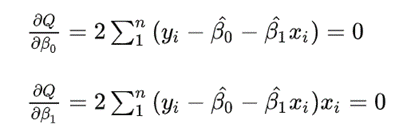
（3）

xi，yi（i=1,2,…n）都是已知的（xi单片机采集的，yi高精度万用表采集的），全部代入上面两个式子，就可求得β^0和β^1的值啦。这就是最小二乘法，“二乘”是平方的意思。

上面（3）求解得到

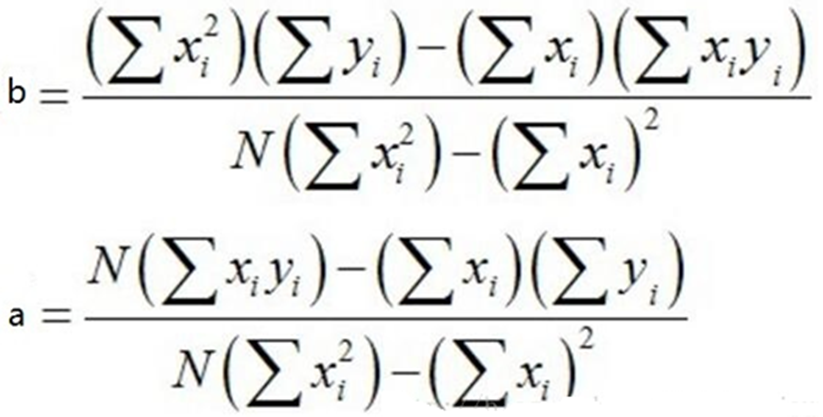
（4）

飞鱼上学那会用matlab采集的部分数据做了个简单的拟合如下图所示：

大家最关注的还是单片机如何编程，下面是该算法的核心实现。

代码实现

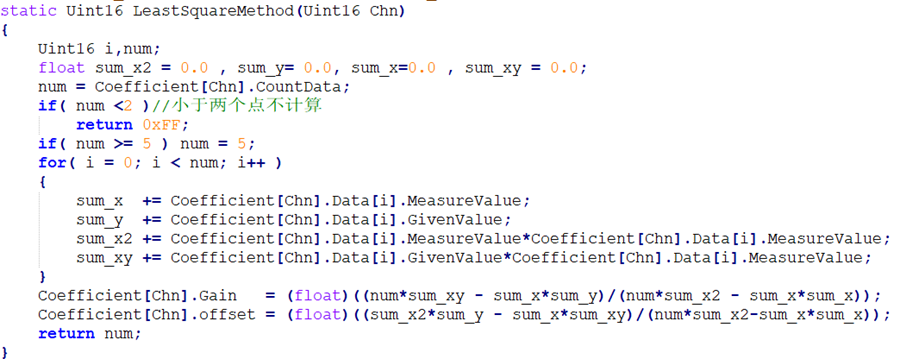
该算法可以对多个ADC通道进行最小二乘最优估计，这个也是经过飞鱼反复验证的，因为家里条件有限，就不给大家做实验现象的展示了，最小二乘用途广泛，用法灵活，它还可以估计传感器的量测误差。

编辑：黄飞