为什么复数不能够排序？

一、前言

在任何一本讲解复变的教科书中，都会提到“复数”不像实数那样能够排序。头一次听说是，都会感到一头雾水。心想我们是可以找到一种排序的方法，  将复数安排的明明白白的。 比如可以先按照复数的实部排序，   如果实部相同，  则接着按照虚部排序。 比如 Python 中的复数排序命名，  就是按照这个方式实现的。 实际上，也可以先按照复数的模进行排序，  接着在按照相角进行排序。 

但数学中所讲到的排序，  是指在一定“数域”内的排序， 也就是在满足元素之间特定操作之后排序不能够产生矛盾。 在复数中定义了加法、乘法等操作。 所定义的排序还应在这些操作下不产生矛盾。

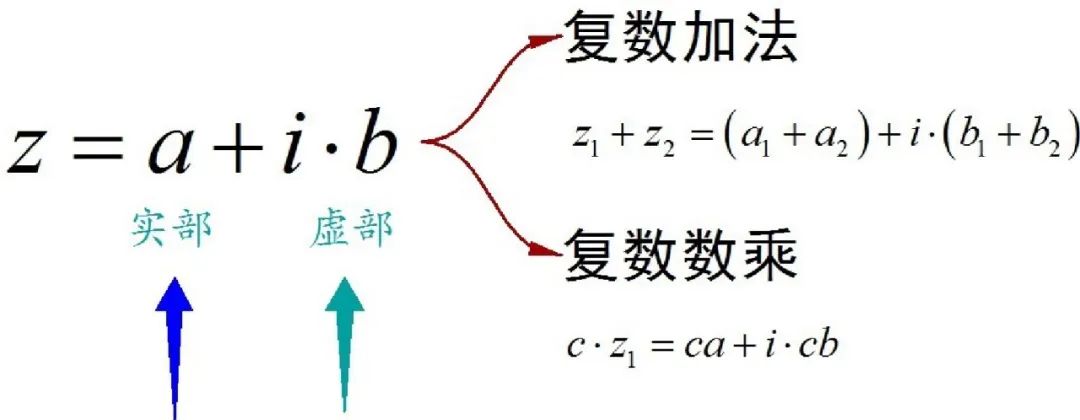
▲ 图1.1.1 复数排序

二、排序矛盾

数学上，对于复数排序的定义需要满足以下性质。 

1、当 a b 属于复数， 那么它们之间的排序必须属于这三种情况之一。

2、当 a 小于 b时， 它们都加上任意一个数字，结果的顺序仍然保持。 

3、当 a 小于 b 时， c 是大于 0 的数字。 它们同时乘以 c， 结果的顺序仍然保持。 

4、最后一个性质，则是任何排序方法都必须满足的相容性。如果 a 小于 b， b 小于 c。 那么 a 小于 c。 

下面按照这四个性质来证明复数无法排序。   实际上只要证明复数中存在两个数字，它们之间的排序无论怎么定义，都会在上面四个性质中产生矛盾。

 

比如，取复数中两个数字， i 和 0。 它们之间的关系也必须满足三种顺序之一。 因为已知这是两个不同的复数。 所以 i 与 0 的顺序只有两种。 

如果假设 i 大于 0。 根据性质三， i 乘以 i 的结果应该是大于 0 乘以 i。 根据复数运算法则，由此可以得到 负1 大于 0。请注意，到此并没有导出矛盾，  因为我们正在讨论复数的排序方法，  所以并不能够按照实数的大小定义复数。 负一大于 0 只是中间推导的结果。 下面再将 负一 乘以 负一， 便会得到下一个结论， 1 大于0。 此时便于前面的结论产生矛盾。 这说明假设 i 大于 0 不成立。

下面从 i 小于 0 开始， 借助于性质2， 两边同时加上 负 i， 便可以得到 负 i 大于 0， 然后在应用 性质 3， 使用负 i 乘以不等式两边， 根据复数四则运算法则，便得到 负1 大于 0 的结论。 这回到前面证明中的结论， 再往后推导同样得到矛盾的结果。至此，综合上面两个过程， 证明复数无法排序。

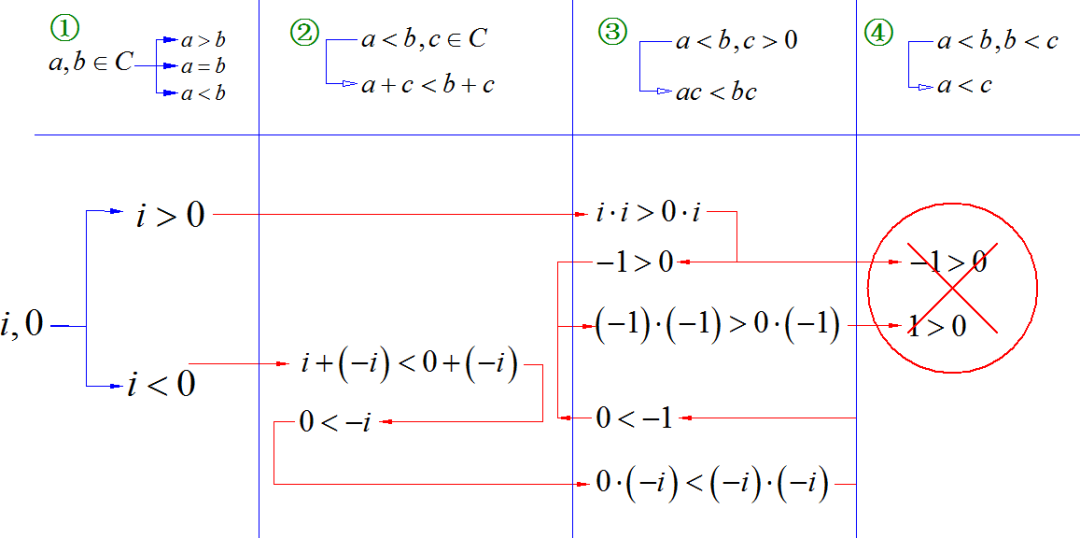
▲ 图1.1.2 矛盾的证明

总  结 

本文对于在复数域内无法排序进行了讨论。 这也让我们对于数学上的排序要求有了更加全面的了解。

审核编辑 ：李倩