轮式移动机器人里程计分析

摘要：本文主要分析轮式移动机器人的通用里程计模型，并以两轮差速驱动机器人的里程计计算为案例，给出简化后的两轮差速驱动机器人里程计模型。

01

引言

里程计是机器人导航系统中非常重要的一环，那么何为里程计？

里程计，可简单理解为记录机器人在一段时间内的运动状态，是基于时间戳的数据帧，该数据帧包含机器人位置、姿态及运动速度、角速度，具体结构对应下图 1.1。

图 1.1 ROS里程计数据结构

里程计的英文单词是Odometry，在ROS小车坐标系树里面有一个里程计专用坐标系，叫做Odom。

但凡涉及到可移动的机器人的导航系统，大概率会涉及到里程计的计算，比如轮式移动机器人、无人机、无人艇，以及多足机器人等，而计算里程计的方案也有很多种，比如基于编码器合成里程计的方案、基于视觉的里程计方案（ORB SLAM）、基于激光雷达的里程计方案（Hector SLAM）、基于IMU的里程计方案，以及多传感器融合的方案。

本文主要以轮式移动机器人为载体介绍基于编码器合成里程计的方案，这是非常经典常用的里程计计算方法之一，在轮式移动机器人领域有着广泛的应用。

02

里程计模型分析

从图 1.1可以看出，里程计主要包含的信息有两部分：速度和位姿，因此接下来将从这两个方面展开介绍。

2.1  速度计算

2.1.1 轮速计算

轮式机器人的驱动轮是由伺服电机驱动的，而电机转轴后安装有编码器，通过编码器采集的数据可以计算出电机输出轴转过的角度。

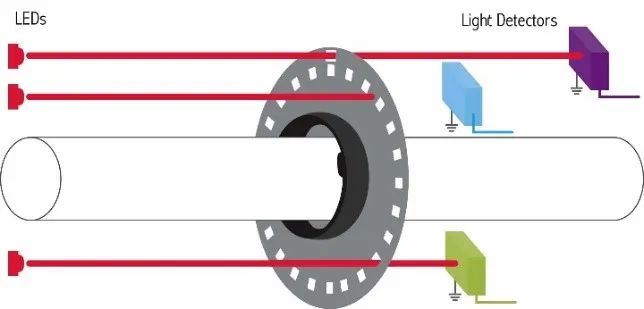
（a）编码器结构

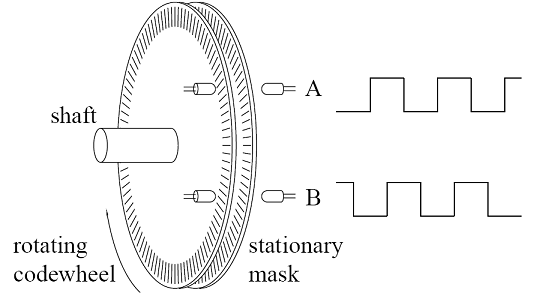
（b）编码器输出波形

图 2.1 光电编码器原理

编码器的种类很多，比如增量式光电编码器（图 2.1），红色的光源是固定不动的，当光栅（图中灰色带孔圆盘）转动的同时，其电路结构会输出A、B两相的方波，使用单片机GPIO的中断模式可采集到方波边沿，进而进行计数，当电机轴转动一圈，可获取总计数为N（可能是512、也可能是1024，这与编码器分辨率有关）。

假设编码器在t1时刻的计数是n1，经过△t时间后，在t2时刻的计数是n2，因此可知电机转轴在△t时间内转过的角度△φ，表示为

那么角速度便可表示为

轮直径是可以直接测量出来的，但需要校准（可参考《常见移动机器人轮直径校准》），则可计算出驱动轮转动的线速度v，可表示为

式中，dw为轮直径。

这样就可以将所有驱动轮的线速度计算出来，如果驱动轮与地面之间没有相对滑动（也就是打滑），那么该线速度也就是驱动轮在地面上的运动线速度。

2.1.2 Odom速度计算

Odom坐标系一般与建立机器人运动学模型时的坐标系相同，也就是机器人零半径转弯的旋转中心为坐标系原点，具体可参考《常见移动机器人运动学模型总结》。

需要注意的是，Odom是一个运动的坐标系，会随着机器人的运动而运动，但是Odom记录的是运动过程中的Odom坐标系状态参数（速度、位姿）是在初始位姿的Odom的坐标系中描述的，如下图所示：记录的是Odom(tk)在Odom(t0)坐标系下的位姿和速度。

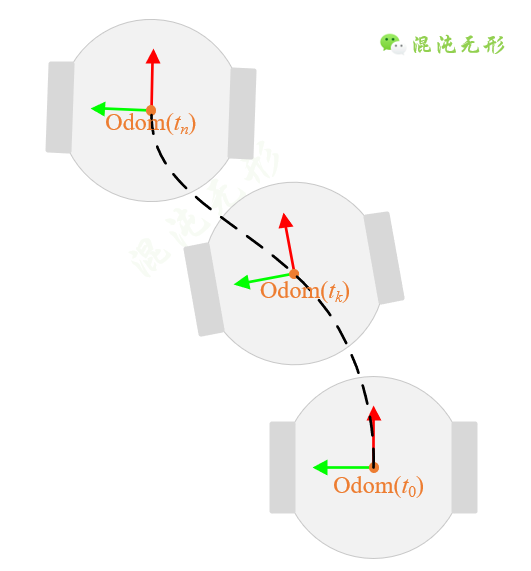
图 2.2 差速驱动机器人运动及其轨迹

这里需要正运动学模型来计算Odom坐标系原点的运动速度，以两轮差速驱动机器人为例，可表示为

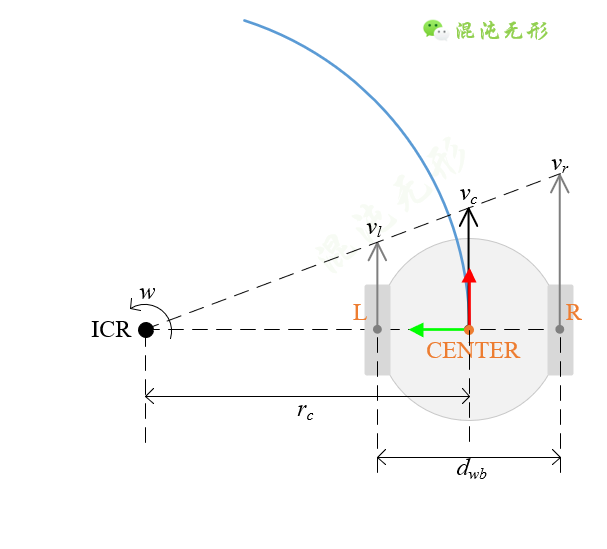
图 2.3 两轮差速模型.机器人的外轮廓可视为圆形，直径为dwb，ICR表示瞬时旋转中心，蓝色圆弧表示机器人运动路径，点L和R分别为左右轮与地面的接触点。

运动学模型写为

其中，vr和vl分别表示两驱动轮的线速度，是可以通过章节2.1.1中的方法计算出来的，因此几何中心的线速度vc和角速度w就可以通过公式（4）计算出来。公式（4）中的vc也就是Odom坐标系x轴的线速度vx，由于两轮差速驱动机器人的非完整性约束（具体分析可参考《两轮差速驱动机器人运动模型及应用分析》），线速度vy和vz均为0，而公式（4）中的角速度w是Odom坐标系z轴的角速度wz，其余角速度wx和wy均为0。

从公式（4）中可以看出，除了前面提到的轮直径需要校准之外，还需对轮间距dwb进行校准，由此实现

由此，图 1.1中的的Odom结构体中的Twist子结构体可写为

表 2‑1 两轮差速驱动机器人Twist信息

 

	linear	angular
x	vc	0
y	0	0
z	0	w

 

以上是两轮差速驱动机器人的速度计算思路，而麦轮移动平台与之不同，属于全向移动机器人，是包含3个自由度，对应的运动学模型也是不一样的，写为

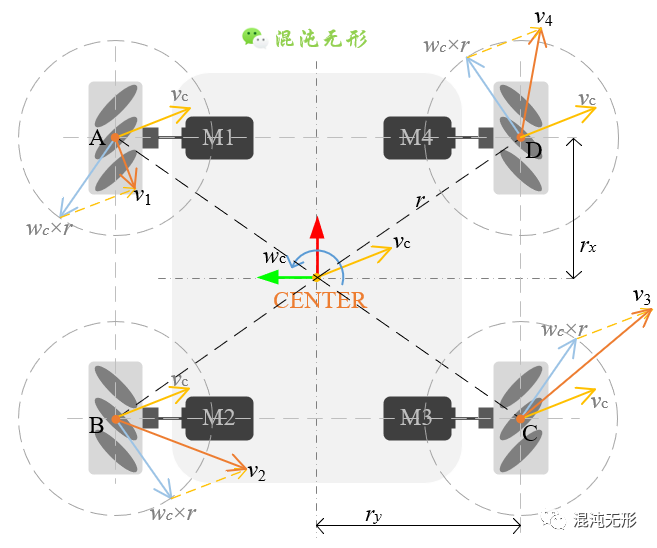
图 2.4 麦轮平台运动分解示意图. 图中r表示中心点CENTER到麦轮与地面接触点之间的距离，rx和ry分别表示r在CENTER坐标系x轴和y轴上的投影距离（均为正值）.

采用同样的思路，计算出四个驱动轮的线速度，结合公式（5）便可得到麦轮平台中心的速度信息。

由此，图 1.1中的的Odom结构体中的Twist子结构体可写为

表 2‑2 麦轮移动平台Twist信息

 

	linear	angular
x	vcx	0
y	vcy	0
z	0	wc

 

除了两轮差速驱动机器人和麦轮移动平台，均可以通过上述思路计算得到里程计中的Twist信息。

2.2  位姿计算

计算Odom的位姿是依赖于章节2.1.2中的速度信息的，我们知道速度对时间积分就是位移，角速度对时间积分就是转角。而里程计记录的是机器人在某一时间段内的运动轨迹，也就是位姿变换过程（如图 2.2所示），需要用递推方程表示，如果是两轮差速驱动机器人，写为：

式中，[x y θ]分别表示两轮差速驱动机器人在某时刻的位置和姿态角

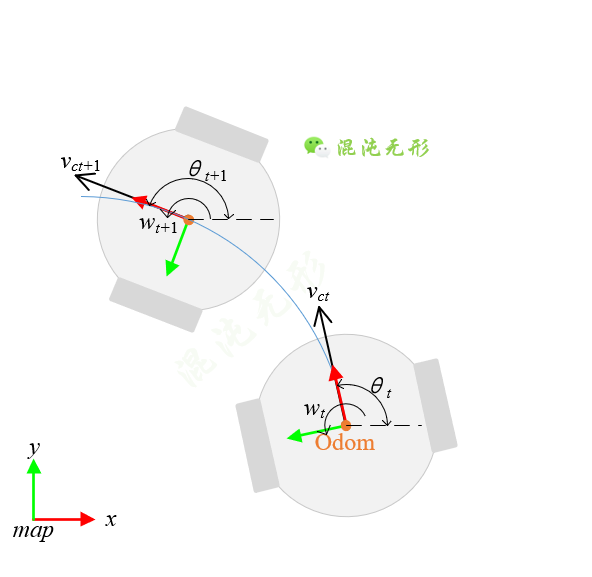
图 2.5 两轮差速驱动机器人运动过程. 蓝色弧线表示运动轨迹

结合图 2.5来解释公式（6），从公式（6）可以看出是做了近似处理，包括：dt时间内假设机器人是以[vc w]的速度进行匀速运动，但实际速度肯定不是匀速运动的，这存在误差；另外，驱动轮可能存在微弱打滑的情况，也会引入误差；最后，两轮差速驱动机器人运动轨迹是圆弧曲线，速度方向是沿着圆弧切线方向的变化而变化的，但这里假设dt时间间隔很短，故“以直代曲”，认为机器人运动轨迹是直线段、速度方向也是不变的，在dt时间内保持着θ的方向，所以也会引入误差。

如果是麦轮移动平台，原理也是和两轮差速驱动机器人一致的，但又有些区别：麦轮平台多了一个自由度，但可以从速度分解（或运动合成）的角度分析

化简为

麦轮移动平台公式也包含了两轮差速驱动机器人的近似处理思想。

综合上述分析，可以计算得到t时刻下机器人的运动速度、位姿信息，合在一起也就是里程计信息了。

03

案例分析

从前面的分析可以看出，在计算速度、位姿时，经过多次运算，位姿计算精度有所降低，此外，计算速度和位姿时，都需要一个时间间隔dt，那么可以从这个dt入手，进一步化简，得到更简洁、优雅的公式。

这里以两轮差速机器人为例，计算化简里程计公式。

假设差速机器人在极短的dt时间内运动了一小节距离，故可视为在dt时间内机器人做匀速运动，如图 3.1所示，在极短时间内做匀速运动，可写为

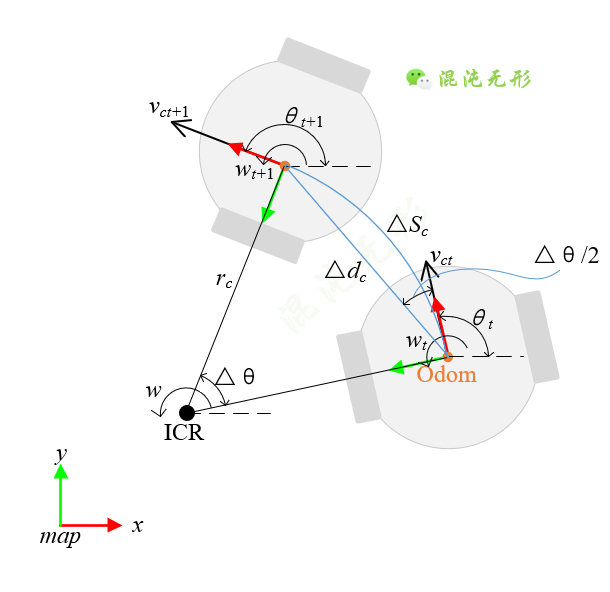
图 3.1 差速驱动机器人里程计示意图

如果机器人做匀速运动，且存在角速度，那么机器人中心的运动轨迹一定是一段标准的圆弧，其长度表示为△Sc，对应的圆心角为△θ，因此有下面的这个关系式

则，左轮和右轮的运动轨迹长度可写为

结合公式（8）和（9），有

为后续计算，这里需要对公式（6）做一个修正，细心的读者可能已经发现问题了，在公式（6）中，方向角使用的是θt，也就是速度vct的方向，这个方向和△dc的方向之间存在一个夹角，这个夹角的大小是△θ/2，使用△dc的方向比速度vct的方向更加准确，因此修正后的公式（6）为

可见，这里还存在一个系统误差，也就是圆弧长度△Sc和直线段长度△dc并不相等，要得到直线段长度△dc，还需要再做一个转换（三角变换，也可以使用余弦定理）

需要回顾的是，这里有个假设，dt时间间隔极短，意味着△θ非常小，所以公式（12）可写作

从公式（13）可以看出，兜兜转转，又回到了公式（8），这里就需要做一个权衡，如果dt时间间隔极短，那么可以取近似值，也就是认为△dc≈△Sc，以直代曲，如果dt时间间隔偏长，那么可以采用公式（12）计算，计算中包含正弦函数，但会降低计算效率、损失计算精度。

这里就采用“以直代曲”的方式来做进一步计算：

通过公式（9）计算△θ，得

将公式（10）和公式（15）带入公式（14），可知

因此，可状态转换方程可写作

从公式（17）可知，仅需要计算左右驱动轮在dt时间内运动过路程，便可得到dt时刻的位姿，回顾到本文的章节2.1.1的轮速计算，根据公式（1）可以计算驱动轮转过的角度，因此可以得到运动的路程

式中，nl1、nl2分辨表示左轮在时间dt前后采集的左轮编码器读数，nr1、nr2分辨表示右轮在时间dt前后采集的右轮编码器读数。

所以，将公式（17）和（18）相结合，仅需要定期采集编码器读数，即可更新里程计中的位姿信息，而速度信息也是可以根据公式（2）和（3），结合运动学模型计算出来。而在实际应用中，编码器采集频率和里程计更新频率保持一致（或整数倍），这样更利于计算，减少重复计算带来的精度损失和时间消耗。

从前面的公式可以看出，要得到更准确的里程计参数，需要对差速驱动机器人的轮直径和轮间距进行校准。

其他的机器人里程计模型也可以参考两轮差速驱动机器人案例，做进一步化简，减少重复计算。

04

结论及展望

本文主要从编码器原理介绍、轮速计算及位姿计算等方面分析了轮式移动机器人的通用里程计模型，并以两轮差速驱动机器人的里程计计算为案例，详细分析了两轮差速驱动机器人运动规律及其位姿变换的等效思想，最后给出了简化后的两轮差速驱动机器人里程计模型。

审核编辑 ：李倩