

电控入门之电机FOC
电子说
描述
我们重点就讲一个事情:
怎么让三相绕组变成我们心里想要的那个电磁铁!
也就是能给出360°任意指向的一个磁场矢量,同时这个磁场矢量的大小我们也能任意控制!
我们先看简单的定子,假设就是三个齿一对极的,因为任何多个齿的都是可以看成是n个3齿的组合,图中有ABC三个绕组,上一节我们说过,两个正交的绕组分别给电可以形成xy坐标下的任意一个方向的矢量,现在这里有三个绕组了怎么实现?
三个绕组分别给电当然是可以的,这是最简单的,因为两个绕组都可以做到,更何况三个绕组呢,但是现实是三个绕组分别给电,我们需要接6个线头,A+和A-,B+和B-,C+和C-,每个绕组的磁力和大小(正反)要控制,都要一个h桥,这样我们就要3个h桥了,这显然是很大的浪费!
H桥控制线圈如下:
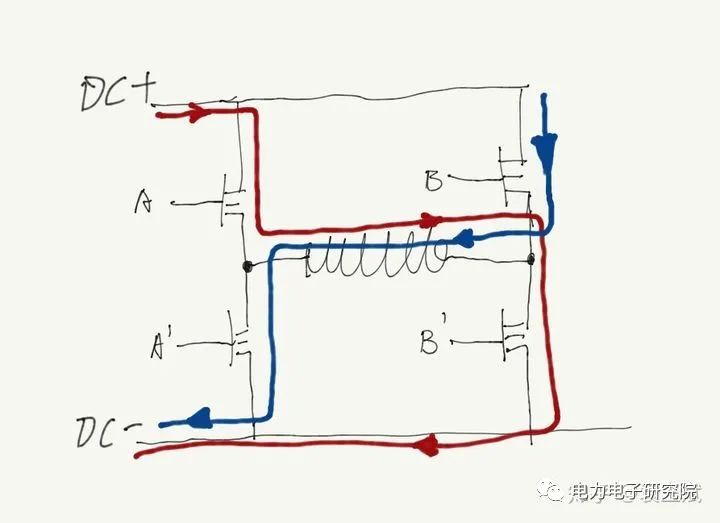
图2
图中,是一个线圈在中间,有4个mos,A和B’打开的时候,线圈电流则是红色箭头方向,B和A‘打开的时候,线圈电流则是蓝色方向,通电罗线圈电流方向和磁力方向就很明显了;红色方向电流产生电时候,改变A和B'同时导通电时间,其它时间mos是全部关闭的,这样能调整DC电压加载在线圈上电有效时间,这就等效成一个小电压加在线圈上了,比如一半电时间A和B'打开,一半电时间所有电mos都关闭,则相当于0.5VDC加在线圈上了,如果全部时间A和B’都是打开的,则相当于VDC加在线圈上了,之所以电压能这样等效的原因是因为线圈是电感,实际线圈上感受到的电压是在VDC和0之间变化的,但是电流是连续的,电流连续,线圈产生的磁场也就是连续的(实际电流也是上升下降的,但是电压变动很快的话,电感够大,理论可以做到电流连续,如下图)
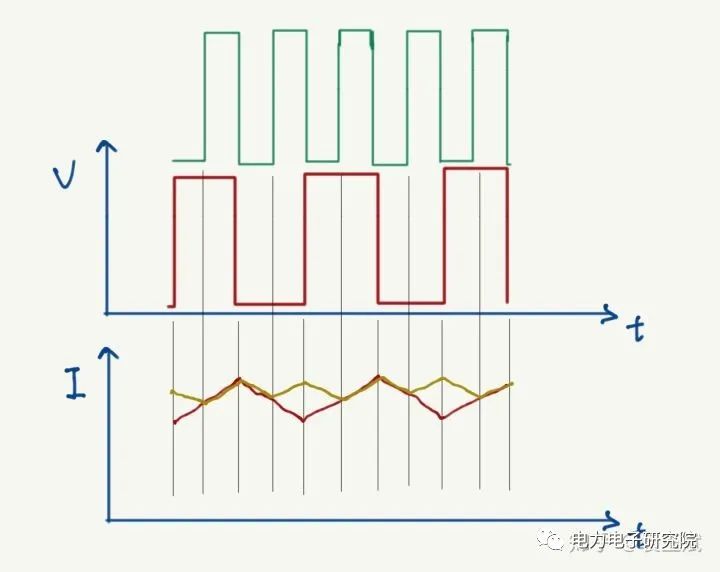
图3
如图电压都是50占空比,绿线和红线,对应的电流就如下图中的黄色和红色,占空比一样的情况下,频率越高,电流波动的峰峰值就越小了(具体电流的高度不深纠,主要示意一下)!
回到上面的ABC三相电图,如果我们分别控制三个线圈,我们要3个H桥,但是前人要聪明的多,假如我们把图1的A-,B-,C-全部连接在一起,然后只控制A+,B+,C+怎么样,这样我们做一下假设,A给高电平,A'给低电平,让这个控制的上边mos打开,下边mos关闭,则有了A+连接DC+;B给低电平,B’给高电平,让这边控制的上臂mos关闭,下臂mos打开,则B+连接了DC-,同理和B一样的操作,让C+连接DC-;------------------方法一

图4
保持上面的这样的接法,这样我们能发现,电流从A进入,B,C流出,如图5的1所示的,
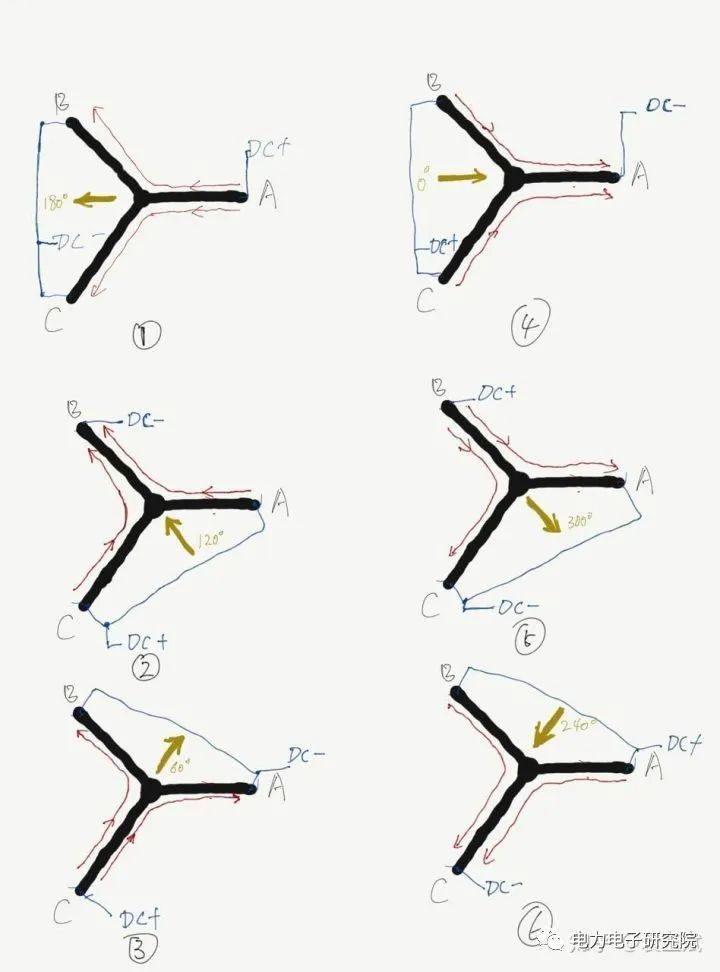
图5
这样橘黄色的箭头方向和电磁铁形成的磁场方向一致,
但是这里我们把橘黄色箭头称呼为电压矢量的方向,因为这里我们加载的是电压方向,A指向B和C,由于是稳态的,所以电流方向也是这个方向,所以磁场方向和橘色箭头一致了,
要是这个橘色电压方向旋转起来后,一般来看,磁场的方向是滞后与这个箭头方向的(不是90°),
因为定子里面是电感-电阻模型,我们知道纯电感中,电流滞后电压90°相位,这里因为有电阻,实际上还有转子永磁反电动势,所以滞后的角度和你的电流大小,频率都有关系,但是我们知道是滞后的就好了;
知道上面的关系,我们这里严谨一点,这一章节我们说这个控制不是控制电磁铁产生360°任意指向的磁场,而是把电磁铁上加载的电压矢量控制到360°的任意指向,同时控制这个电压矢量的幅值,
电压矢量的方向任意控制了,大小任意可以控制了,相信电流矢量的方向和大小当然也是可以任意控制了,我们先研究电压矢量方向大小任意控制;
这样我们回到图5,重复图5中1的操作,我们可以复制出来2,3,4,5,6的操作,这些操作就是重复图4中的 方法一, 但是改变了mos管子接通的上下关系,这样我们就得到了6个状态了,图5中我标注出来了,大家仔细看会发现这6个状态的方向依次是差60°的方向,如果我们把通电的顺序按照,4,3,2,1,6,5,4这样动起来,你看看是不是出现了旋转的电压矢量了!

图6
没错啊,这就是我们的6个旋转电压矢量,这也是有感的方波里面,人家常用的伎俩,
简单的描述,就是连续的给这样的6个方向的接通时序,假如他检测到电机的转子d轴(电控入门一中解释了d轴)在0度的位置,它就给120°这个电压矢量,转子d轴到了60°,它就给180°的这个电压矢量,如此一步一步的来控制电机旋转,也就是我们大家常常说的6步换向,
六步换向也是可以控制这个电压矢量的幅值的,它控制幅值的方式是图4的方法一中,控制B,C连接的下臂mos一直导通,但是A连接的上臂mos不断的 开关 ,当A连接的上臂mos关闭的时候,A和DC+断开了,DC+-电压加不到ABC上,是高阻态,只有A连接的上臂mos导通的时候,DC+-,才能加载在ABC上,这样控制开关的占空比,则能够控制的了电压矢量的作用时间,微观来看,就是有-无-有-无-有这样夹在一起,控制这个有无的时间比重就控制了电压矢量的等效幅值了, 简单的说就是在插入了断路时许到通路时序中 ;(实际断路时序中,看图4,A相的上臂mos管,下臂mos管都关了,但是A相里面还有电流,电流从哪进入A相的呢,电流是从A相连接的半桥的下臂mos管的体二极管里由下向上流动的,也就是俗称的续流)-----------------------方法二
多说一句,这里说等效的电压矢量幅值,为什么是等效,因为电感模型中,电压是可以突变的,但是电流是不能突变的,如果你拿示波器去夹在A和星接点上,看A相的分压,你会发现,这个分压就是有无有无的节奏,但是如果你拿电流钳钳在A相上看电流,你会发现这个电流是一直在的,只是有点波动,三角锯齿波的形状的波动,开关的频率越高,电流波形频率也越高,波动幅度越低,也越接近直流,电流是连续的,所以电压我们这里说等效,这也是伏秒原则的缘由;
而这里我们要用的是svpwm,会更加有趣,有趣在哪里?
1.svpwm就是我们要脱开这有限的6个方向,我们要制造无限个连续的方向填充满360°,
2.svpwm的调整电压矢量的等效幅值,是通过插入主动短路的零矢量作用时间来完成,而不是 断路 ;
主动短路的零矢量就是方法二中的A相的上臂mos关闭,下臂mos也关闭,变成A相的下臂mos打开;B,C相的下臂mos也打开,想想会有什么问题吗?肯定没有问题啊,原来方法二中,你想把A相的上臂mos关闭,A相的下臂mos本来就是关闭的,但是奈何这个下臂mos不争气,身体里面有个反骨(图4),这个二极管,它就给你把电导通了,那如其这样,还不如我主动给你下臂的mos给打开呢,对不对!这个一打开就是A,B,C的下臂mos都是开了上臂mos全关闭,这就是我们说的零矢量,
那爱思考的同学想说,为啥不有A,B,C的上臂mos都打开,下臂mos都关闭行不行?
聪明,当然可以的,你已经抓到了另外一个零矢量了,
这样2个零矢量,结合6个不同方向的电压矢量,一共你找到了8个可控的通电时序了,这8个通电时序,有机的组合在一起,将能构成奇妙的svpwm;
我们提到了8种通电时序,我们做个规定,每一相的半桥,什么是半桥?图4的A和A'这两个所在的mos构成的叫做A相半桥,上臂的mos打开下臂的mos关闭,我们记作1,上臂的mos关闭,下臂的mos打开我们记作0;
有没有上下臂的mos同时打开的情况?没有,这样会短路;
有没有上下臂mos同时关闭的情况?svpwm中除了上臂mos管关闭,下臂mos管还没打开,或者下臂mos管关闭,上臂mos管还没打开的死区内,其他情况下没有,而六步方波中是存在的!
我们把上臂mos管简单的称呼一下叫做上管,下臂的mos管叫做下管,有A,B,C三相,每一相有两种可能,一起排列组合有2^3种可能,这样上下管的8种搭配就是:
方便阅读,我把图6再搬到这里

图6
(0,0,0) A下管打开,B下管打开,C下管打开,对应图6中的中心点
(0,0,1) A下管打开,B下管打开,C上管打开,对应图6中的60°
(0,1,0) A下管打开,B上管打开,C下管打开,对应图6中的300°
(0,1,1) A下管打开,B上管打开,C上管打开,对应图6中的0°
(1,0,0) A上管打开,B下管打开,C下管打开,对应图6中的180°
(1,0,1) A上管打开,B下管打开,C上管打开,对应图6中的120°
(1,1,0) A上管打开,B上管打开,C下管打开,对应图6中的240°
(1,1,1) A上管打开,B上管打开,C上管打开,对应图6中的中心点
以上说到的上管打开,默认的下管就是关闭,下管打开,默认的上管就是关闭;
以上的每个组合看作一个矢量,于是有了这8个基础矢量,8个基础矢量怎么构成平面内任意方向的矢量?比如我们想让电压矢量指向24°,怎么办?--------------------问题1



SVPWM的基本思想也是这样,
1.用6个非零的矢量的相邻的两个矢量来控制合成矢量的方向,
2.用零矢量来调整合成矢量的幅值
回到问题1,产生24°方向的矢量,我们要使用图6中的0°和60°两个非零基础矢量来合成,然后24°方向的矢量的幅值我们用零矢量的掺入来调整;
非零基础矢量的模长是多长?
我这里用矢量变换的原则,比如说基础的非零矢量(0,1,1)的模长表示多大?
矢量合成,看图5的第4个,方便阅读,我这里再插入一次

图5





图8(网扒,侵删)
上面我们提到的ARR和CCR是stm32中的概念,这个图里面的PTPER就是我们说的ARR, PDC1,2就是我们说的CCR1,2,几个通道就有几个CCR,看图计数值从0开始爬到PTPER,然后在爬升的过程中,PDC1遇到后,PMW1H就发生了一次翻转,然后在计时器从PTPER下降的过程中,遇到了PDC1,PMW1H也发生了一次翻转,这样这个PMW1H通道就在一个周期T内发生了两次状态改变,1-变到0-变到1,这里的T就是计数器从0爬到PTPER再降低到0的这个过程的时间;那么再看,你改变了CCR值也就是图8的PDC1, 2值,是不是就能实现控制了PWM1H, PWM2H的波形了,这个波形最终是产生出来我们上文提到的24°或者其他方向的一个确定模长电压矢量;
FOC周期和这个PWM周期T怎么理解呢 , 一般来看 :
FOC的运算要在这个PWM内做出改变CCR值,也就是图8的这个PDC1,2值,
有的人呢会在一个PWM周期内,做两次FOC,也就是每一半的PWM周期内,它都会计算出一个新的CCR值,然后在下半个PWM周期开始的时候就应用了这个新CCR值,这种就是FOC频率是PWM频率的两倍,
有的人是一个PWM周期内,做一次FOC,这样FOC频率就和PWM频率一样了,
有的人呢是多次PWM周期内,才做一次FOC,这样呢就是FOC频率比PWM频率低了,
但是FOC频率最快,也不会比PWM频率高出一倍,那是极限了,否则FOC计算出来的CCR值没办法在PWM内得到有效的应用
图8的这种中心对称是可以的,对称中心PWM1H,2H都是00的状态,我们也有别的方案的中心对称,我这里就使用对称中心是1,1的状态;
我们继续回到两个Udc的非零矢量合成24°方向的矢量的问题:
解释了T的含义了,然后我们看t1,t2多大,我们根据这个矢量的合成,列出一个公式,看图7,为了方便阅读,我这里再插入图7:

图7

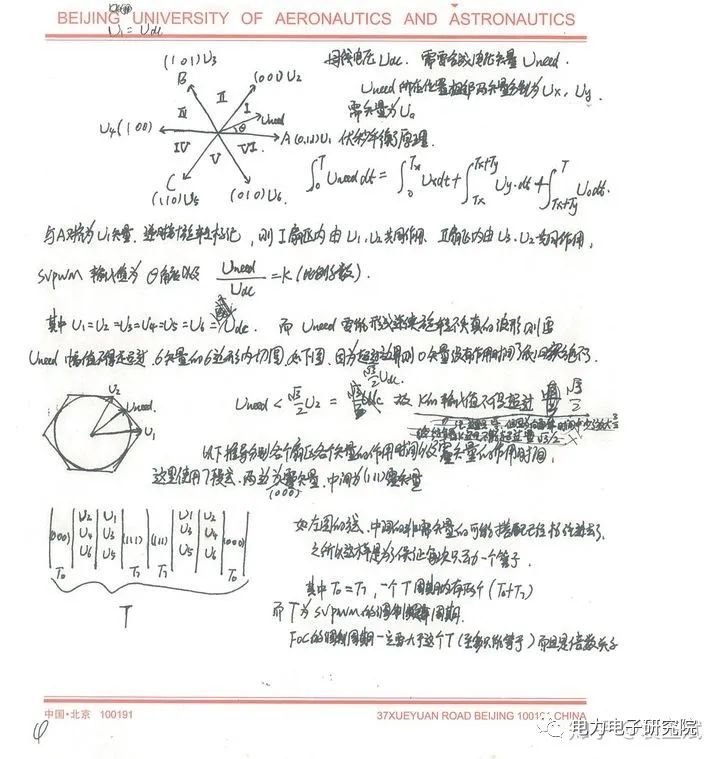



最后的结论就是:给定一个角度,和幅度的电压矢量,可以获得对应的单片机的三个定时器通道的CCR值,
这里补充一点,草稿中的P1和P2是指对应两个非零矢量在一个7段式的周期里面,分别工作的总时间,为什么说总,因为中心对称,前后各一半;PHA,PHB,PHC就是对应的定时器的ABC通道从哪个计数值开始翻转的意思;
其实到了这里,有心的朋友完全可以自己推导出来一个极坐标下的svpwm生成的函数了,
alpha和beta的坐标下的,实际是这个极坐标下的计算中的一个中间过程,可以从极坐标的程序中化简推导出来的,
这里用极坐标,是为了方便后续直观的看到一个旋转电压矢量的作用效果的!
真的做FOC,你还是需要alpha和beta输入的svpwm函数;
PS.( 上面的手稿中推导的式7段式的svpwm,为什么说式7段式,因为你看手稿第四页啊,我的每个扇区的情况中都做了8段分割,而最中间的是1,1,1(从上往下看),我给分了两次,这是为了好计算理解用的,实际是因为是一样的状态,所以其实有7个段,所以这叫做7段式,同理,如果你把中间的1,1,1全部摘掉,这样原来1,1,1,两端的矢量是不是可以直接推一起了,拿手稿第四页的第一扇区举例子,中间是不是就变成了U1在一起,这样一下子少了两段,所以就变5段式了,对应的时间公式,你看利用P1,P2是不是还是很容易就能计算出来了;这里我们一般5段式会摘掉1,1,1留下0,0,0是为了方便下桥臂电流采样,和降低上桥臂的栅极驱动器的自举负担,这样显然也会导致下桥臂的负担多些,你当然可以摘掉0,0,0只留1,1,1,你还可以周期性的0,0,0和1,1,1一个来一次。 )
-
从零开始之电机FOC控制2025-04-23 4370
-
FOC电机与传统电机的区别2024-11-21 1610
-
foc可以控制哪种电机 foc电机库怎么调试2023-06-10 5567
-
手把手教你无感FOC电机控制2023-06-09 9559
-
【硬声推荐】电机FOC控制视频合集2022-12-14 3503
-
【老手经验】FOC电机控制究竟该如何学习?2021-09-01 4311
-
DSP电控成长之路2019-04-09 3892
-
电机:交流感应电机FOC、无传感器FOC和观测器的介绍2018-08-21 11702
全部0条评论

快来发表一下你的评论吧 !

