

晶体管负反馈放大电路的参数设计
模拟技术
描述
放大倍数的推导
我们假设的电路在没有负反馈的时候,电路增益为A(也称为开环增益,或者裸增益,等于各极增益的乘积)。实际放大倍数Av可以表示为:
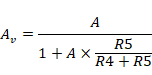
这个公式可以推导出来,但推导的过程没有这么重要,我简单记录在这里,不理解也没有关系,因为后边使用到运算放大器的时候,“虚断”与“虚短”结合,即便不理解推导过程也不影响使用。
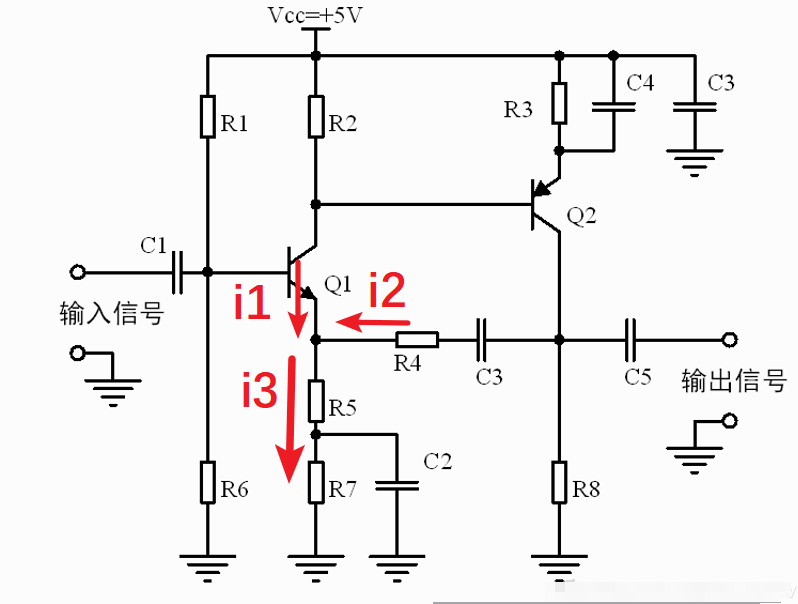
以下的所有推导过程都只考虑交流通路,因为放大的本来就是交流信号。
设输入信号Vi,输出信号为Vo,开环增益为A,实际增益为Av,其中 Av= Vo/Vi
分析R4与R5的连接点,电流的关系
电阻R4是反馈电阻,流过R4的电流i2可以表示为:
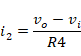
流过R5的电流i3可以表示为:
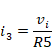
对于R4与R5连接点的电流情况分析,可知:
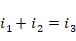
i1的理解比较麻烦,要假设电路是开环工作,没有负反馈,当输出电压为Vo的时候,应该输入的电压为Vi’。
Vi’=Vo/A
这个假想的输入电压在到达R4与R5的连接点的时候,感受到的电阻就是R4//R5
i1=(Vo/A)/(R4×R5/(R4+R5))
所以
Vi/R5=(Vo-Vi)/R4+(Vo/A)×((R4+R5)/(R4×R5))
整理成Vo/Vi的格式得到:
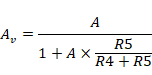
实用的放大倍数公式
R4是反馈电阻,令β=R5/(R4+R5),那么放大倍数可以表示为:
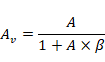
β表示有多少输出返回到了输入,称为反馈率。上述公式是非常重要的一个公式,不仅适用于此处的晶体管负反馈放大,也 能够应用到运算放大器中。如果认为开环增益A非常大,那么反馈率几乎就是放大倍数的倒数:
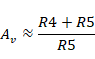
注意,前提是开环增益A非常大。因此电路设计中,要时刻注意,想办法让开环增益尽可能的大一些。
不难看出,省略的是上述公式中的i1,因为A很大,Vo一定,所以Vi’很小,所以就把i1忽略了。这也是使用运放芯片时所谓的“虚断”。认为由于i1这个电流太小所以忽略。
为什么是“负反馈”?
下图是简化以后的交流工作情况,可以帮助我们分析负反馈的工作情况。
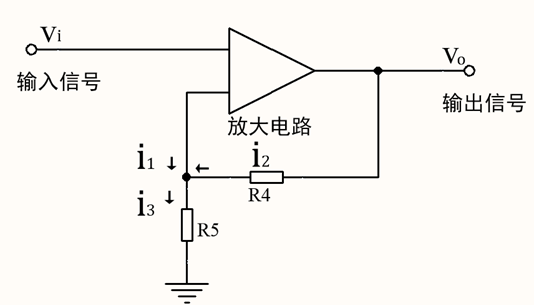
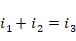
假设输入信号vi不变,因为某种情况,导致了输出信号vo变大,那么:
i2变大,i3不变,导致i1变小;
i1变小相当于放大电路的输入信号变小,所以Vo变小,所以Vo可以保持相对稳定的值,电路进行负反馈调节。
确定电阻与电位
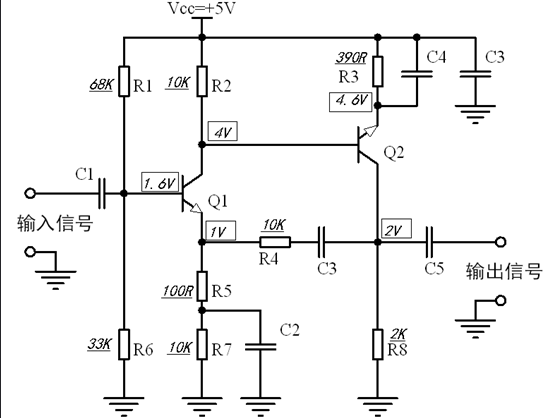
这个电路的电阻比较多,但是确定电阻的过程并不复杂,主要在于确定电路的直流电位与工作电流。
为了使开环增益尽可能的大,可以把第一级的很大倍数设置为100倍,那么R2是R5的100倍。
设IC1为0.1mA,VE1=1V,那么可以算出R5+R7=10K,取R5为0.1K,R7为10K。
则R2=100×R1=10K,此时VC1=1V。
也可以算出R4=10K。
由VE1=1V可以得出VB1=1.6V,取偏置电路的电流为0.05mA,可分别取R1=68K,R2=33K。
由VC1=1V可以得出VE2=0.4V,取IC2为1mA可以算出R3≈390Ω。
VB2=VC1=1V,理论上来讲第二级的集电极还有4V的电压范围,R8决定输入为0时的电压,可取VR2=2V,取IC2为1mA可以算出R8=2K。
输入与输出阻抗
输入阻抗同共射极放大电路,是R1//R6 。得益于较小的IC1,所以偏置电路的电流也无需太大,此处取值为0.05mA,所以偏置电路的电阻足够大,输入阻抗也足够大。
看上去输出阻抗就是R8的阻值。但实际上我们提到过,负反馈使得电路的性能提升,输出阻抗也会变小,所以我们可以连接合适的负载,通过观察空载输出波形的幅值与带负载(未失真的)波形幅值来计算输出阻抗。
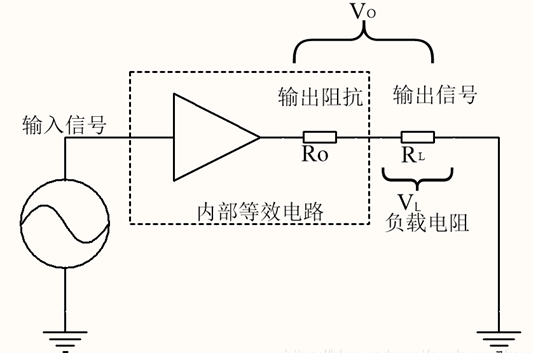
图 负反馈电路输出阻抗测量图
假设电路的输出阻抗为Ro,连接负载RL以后,输出的波形幅值从Vo变成了VL,那么根据欧姆定律,不难分析出:
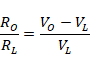
负反馈放大电路可以减小输出阻抗。事实上,如果开环增益是增加反馈后增益的x倍,那么最终的输出阻抗就是没有增加反馈时输出阻抗的1/x。
放大波形观察
观察Q11集电极波形,发现相比于单纯的共射极放大电路,有一点失真,原因在于相当一部分电流流向了第二级,并从反馈回路返回到Q1发射极。
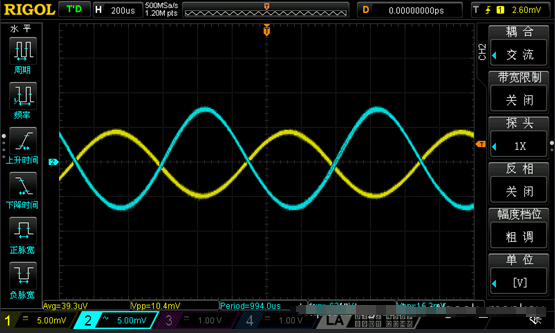
对比输入与输出波形,大致是100倍放大,可以看出相位相同。因为一级共射放大相位相反,第二级放大相位再次相反,最终结果相位相同。
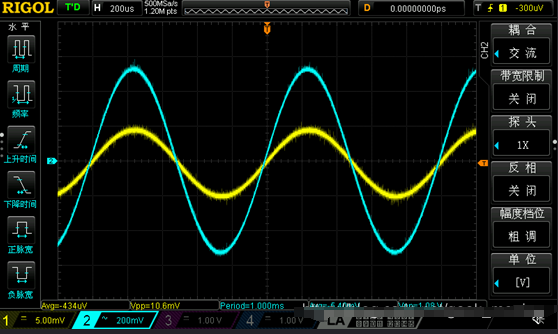
-
负反馈放大电路内参数“应变”分析2011-01-06 714
-
负反馈式的宽带放大电路图模块设计2014-10-08 2489
-
晶体管放大器设计2009-03-20 9891
-
晶体管电路设计丛书上册2009-11-20 13344
-
入门经典:晶体管电路设计上下册让你感性认识晶体管2017-06-22 98797
-
【下载】《晶体管电路设计》——晶体管电路基础知识汇总2017-07-25 38543
-
四种负反馈放大电路及其反馈判断方式,工程师必懂!2020-09-02 4376
-
晶体管低频放大器相关资料推荐2021-06-02 1962
-
负反馈放大电路的分享2022-01-25 1773
-
为什么说RE对每个晶体管的共模信号有2RE的负反馈效果呢?2023-04-25 1298
-
负反馈放大器2010-04-16 6469
-
负反馈对放大电路性能的影响2015-11-13 1316
-
实验四 负反馈放大电路2021-11-30 1823
-
简述负反馈对放大电路的影响2024-07-30 3431
-
负反馈放大电路的含义是什么2024-08-15 2393
全部0条评论

快来发表一下你的评论吧 !

