线性稳压器的关键技术及主要参数

4.线性稳压器的关键技术

所有的电压稳压器都使用反馈回路以保持输出电压的稳定。反馈信号在通过回路后都会在增益和相位上有所改变。一般通过在单位增益（0dB）频率下的相位偏移总量可以确定回路的稳定性。对于任何高增益反馈环路来说，环路增益传递函数中极点和零点的位置都决定其稳定性。

为了了解稳定性需要使用波特图（Bode Plots）（图4.1），它将回路的增益（dB）表示为频率的函数。波特图是很方便的工具因为它包含判断闭环系统稳定性的所有必要信息。为了从波特图中获得必要的信息需要先了解几个关键点：环路增益（loop gain），相位裕度（phase margin）和零点（Zeros）、极点（poles）。

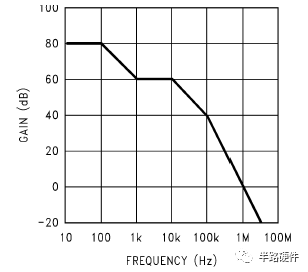
图4.1 波特图

4.1.环路增益（Loop Gain）

每个闭环系统都有个特性叫做环路增益。在稳压器的分析中，环路增益定义为反馈信号通过整个回路后的电压增益。为了更好的解释这个概念，将图3.5LDO的框图修改为如下图所示：

图4.2 环路增益示例图

变压器用来将AC信号发射到‘A’、‘B’点间的反馈回路。利用这个变压器，小信号正弦波来调制反馈信号。测量A、B点间交流电压并用来计算环路增益。 环路增益定义为两点电压的比：

Loop Gain ＝ Va/Vb

特别需要注意的是，从Vb点开始传输的信号通过回路时会出现相位偏移，最终到达Va点。相位偏移的多少决定了回路的稳定性。

所有的稳压器都用到了反馈以使输出电压稳定。输出电压是通过电阻分压器进行采样的（如图4.2），并且该分压信号反馈到误差放大器的一个输入端。

因为误差放大器的另一个输出端连接到一参考电压源上，误差放大器将会调整输出到调整管的输出电流以保持DC电压的稳定输出。 必须要注意，为了达到稳定的回路就必须使用负反馈（negative feedback）。负反馈（有时称为degenerative feedback）就与源信号的极性相反（如图4.3）。

图 4.3

由于与源的极性相反，负反馈总会阻止任何的输出变化。也就是说，如果输出电压想要变高（或变低），回路总会阻止其到正常值。 正反馈（Positive Feedback） 当反馈信号与源信号有相同的极性时就会发生正反馈。此时，回路响应会与发生变化的方向一致。这样明显不能达到稳定，因为不能消除输出电压的改变，反而将变化趋势扩大了。很明显不会有人在线性稳压器件中使用正反馈，但是如果出现180°的相移，负反馈就成为正反馈了。

4.2.相位裕度

讲相位裕度之前需要先解释相位偏移。相位偏移就是反馈信号经过整个回路后出现的相位转变的总和（相对起始点）。相移（用度表示）通常使用网络分析仪（network analyzer）测量。

图 4.4 相移图

理想的负反馈信号与源信号相位差180°（如图4.4），因此它的起始点在-180°。在图3.3中可以看到这180°的偏置。也就是波型差半个周期。可以看到，从-180°开始，增加180°的相移，就会使信号相位回到零度。这也就使反馈信号与源信号相位相同了，并使回路不稳定。

相位裕度（单位为度）定义为在环路增益等于0dB时，反馈信号总的相位偏移与－180°的差。一个稳定的回路一般需要20°的相位裕度。相位偏移和相位裕度可以通过波特图中的零、极点计算获得。

4.3.极点

极点就是增益曲线中斜率为－20dB/十倍频程的点。每添加一个极点，斜率增加20dB/十倍频程。增加n个极点，n×（－20dB/十倍频程），如图4.5。

每个极点表示的相位偏移都是与频率相关的，相移从0到－90°（增加极点就增加相移）。最重要的一点是几乎所有由极点（或零点）引起的相移都是在十倍频程范围内。注意：一个极点只能增加－90°的相移，所以最少需要两个极点来到达－180°（不稳定点）。

图 4.5 极点增益/相位图

4.4.零点

零点（如图4.6）在增益曲线中斜度为＋20dB/十倍频程的点。

图4.6 零点增益/相位图

零点产生的相移为0到＋90°，在曲线上有＋45°角的转变。首先要知道的是零点就是“反极点”，它在增益和相位上的效果与极点恰恰相反。这也就是为什么要在LDO的回路中添加零点的原因：它可以抵消极点的效果，否则电路会不稳定。

4.5.线性稳压器的稳定性分析

下面用一个包含三个极点和一个零点的波特图（如图4.7）来分析增益和相位裕度。假设直流增益为80dB，第一个极点发生在100Hz处。在此频率时，增益曲线的斜度变为－20dB/十倍频程。 1kHz处的零点使斜度变为0dB/十倍频程，到10kHz处增益曲线又变成－20dB/十倍频程。在100kHz处的第三个也是最后一个极点将增益斜度最终变为－40dB/十倍频程。

图 4.7 带有相位信息的波特图

也可以从图中看到单位增益点（0dB）交点频率是1MHz。0dB频率通常称为回路带宽（loop bandwidth）。 相位偏移图表示了零、极点的不同分布对反馈信号的影响。为了产生这个图，就要根据分布的零极点计算相移的总和。在任意频率（f）上的极点相移，可以通过下式计算获得：

极点相移＝ －arctan(f/fp)

在任意频率（f）上的零点相移，可以通过下式计算获得：

零点相移＝ －arctan(f/fz)

此回路稳定么？为了回答这个问题，我们只需要知道0dB时的相移（是1MHz）。根本无需复杂的计算。 前两个极点和第一个零点分布使相位从－180°变到＋90°，最终导致网络相位转变到－90°。最后一个极点在十倍频程中出现了0dB点。使用零点相移公式，该极点产生了－84°的相移（在1MHz时）。加上原来的－90°相移，全部的相移是－174°（也就是说相位裕度是6°）。该回路可能引起振荡。

在实际使用中，线性稳压器需要使用到补偿措施。

4.5.1NPN稳压器的补偿

NPN 稳压器的调整管（见图3.5）的连接方式是共集电极的方式。所有共集电极电路的一个重要特性就是低输出阻抗。也就意味着电源范围内的极点出现在环路增益曲线的高频部分。由于NPN稳压器没有固有的低频极点，所以它使用了一种称为主极点补偿（dominant pole compensation）的技术。此时，在IC的内部集成了一个电容，该电容在环路增益的低频端添加了一个极点（如图4.8）。

图4.8 NPN稳压器的波特图

NPN稳压器的主极点（P1）一般设置在100Hz处。100Hz处的极点将增益减小为－20dB/十倍频程直到3MHz处的第二个极点（P2）。在P2处，增益曲线的斜率又增加了－20dB/十倍频程。 P2点的频率主要取决于NPN功率管及相关驱动电路，因此有时称此点为功率极点（power pole）。

因为P2点在环路增益为－10dB处出现，也就表示了0dB频率处（1MHz）的相位偏移会很小。

为了确定稳定性，只需要计算0dB频率处的相位裕度： 第一个极点（P1）会产生－90°的相位偏移，但是第二个极点（P2）只增加了－18°的相位偏移（1MHz处）。也就是说0dB点处的相位偏移为－108°，相位裕度为72°（非常稳定）。

应该提起注意的是，回路很显然是稳定的。因为需要两个极点才有可能使回路要达到－180°的相位偏移（不稳定点），而P2又分布在高频位置，它在0dB处的相位偏移就很小了。

4.5.2LDO的补偿

基于PNP管的 LDO和基于PMOS管的 LDO的传递函数具有几个影响稳定性的极点：

主极点（图4.9中的P0）由误差放大器决定；它是由放大器的gm通过内部补偿电容CCOMP一起控制和确定的。主极点对上述所有LDO结构都是共同的。

第二极点（P1）由输出电抗（指输出电容和负载电容以及负载阻 抗）决定。这使得应用问题更难处理，因为这些电抗会影响环路的增益和带宽。

第三极点（P2）由调整管附近的寄生电容决定。在相同条件下，PNP功率晶体管的单位增益频率（fT）比NPN晶体管的fT低很多。

图4.9 LDO的幅频特性

如图4.9所示，每个极点产生每10倍频程20 dB的增益下降并且伴随90°的相移。因为这里所讨论的LDO有多个极点，所以如果单位增益频率处的相移达到－180°，线性稳压器会变得不稳定。图4还示出了容性负载对稳压器的影响，其等效串联电阻（ESR）会在传递函数中增加一个零点（ZESR）。该零点有助于补偿其中一个极点，并且如果该极点出现在单位增益频率以下时有助于稳定环路并且保持相应频点的相移低于－180°。

ESR对于维持稳定性可能是至关重要的，特别对于使用纵向PNP调整管的LDO。然而，由于电容器的寄生特性，所以ESR不总是好控制。电路可能需要ESR集中在某个窗口范围内以确保LDO工作在对于所有输出电流都稳定的区域（见图4.10）。虽然原则上选择具有合适ESR的合适电容器（要求频率响应曲线在穿过0 dB之前下降得足够快，并且在达到相关极点P2之前向低于0 dB增益方向减小得足够满）非常困难。实际考虑还会增加更多的困难：ESR随着产品型号变化；大批量生产使用的最小电容值需要进行基准测试，包括最小环境温度和最大负载的极端条件。

图4.10稳定性随输出电流IOUT和负载电容的ESR变化

4.5.2.1使用ESR补偿LDO

等效串联电阻（ESR）是每个电容共有的特性。可以将电容表示为电阻与电容的串联（如图4.11）。

图4.11 电容器的等效ESR

输出电容的ESR在环路增益中产生一个零点，可以用来减少负相移。零点出现的频率值与ESR和输出电容值直接相关：

Fzero＝ 1/(2π×Cout×ESR)

使用上一节的例子（图4.9显示的波特图），我们假设输出电容值Cout＝10uF而且输出电容的ESR＝1Ω。则零点发生在16kHz。

图4.12显示了添加此零点如何使不稳定系统变为稳定系统：

图4.12 用ESR零点稳定LDO

回路的带宽增加了所以0dB的交点频率从30kHz移到了100kHz。到100kHz处该零点总共增加了＋81°相移。也就是减少了PL和P1造成的负相移。 因为极点Ppwr处在500kHz，在100kHz处它仅增加了-11°的相移。累积所有的零、极点，0dB处的总相移现在为-110°。也就是有＋70°的相位裕度，系统非常稳定。 这也就解释了具有正确ESR值的输出电容是可以产生零点来稳定LDO系统的。

4.5.2.2ESR和LDO的稳定性

通常所有的LDO都会要求其输出电容的ESR在一定范围之内以保证稳压器的稳定性。LDO制造商会提供一系列由输出电容ESR和负载电流组成的定义稳定范围的曲线，如图4.13所示，作为选择电容时候的参考。

图4.13 LDO的ESR 稳定范围曲线

要解释为什么有这些范围存在，可以由前面提到的例子来说明ESR的高低对相位裕度的影响。

高ESR

同样使用前文提到的例子，假设10uF输出电容的ESR增加为20Ω。这将使零点的频率降低到800Hz（如图4.14）。降低零点的频率就会使回路的带宽增加，使它的0dB的交点频率从100kHz变到2MHz。 带宽的增加意味着极点Ppwr会出现在带宽内（对比图3.12）。分析图3.14曲线的相位裕度，可以发现如果同时拿掉该零点和P1或PL中的一个极点，对曲线的形状影响很小。

图4.14 高ESR引起回路振荡的波特图

也就是说该回路由发生－90°相移的低频极点和发生－76°相移的高频极点Ppwr共同影响。 尽管还有14°的相位裕度（可能稳定）。但很多测试数据显示，当ESR＞10Ω时由于其它的高频极点的分布（在此简单模型中未表示）很可能会引入不稳定性。

低ESR

具有很低的ESR的输出电容由于一些不同的原因也会产生振荡。继续用前面的例子，把10uF输出电容的ESR降低到50mΩ，则零点的频率会变到320kHz（如图4.15）。

图4.15 低ESR引起的回路不稳定

不用计算也能知道系统是不稳定的。两个极点P1和PL在0dB处共产生了－180°的相移。因为本系统如果想稳定，则零点应该在0dB点之前提供正相移。然而，因为零点在320kHz处，已经在系统带宽之外了，所以没有起到补偿作用。

4.5.2.3LDO输出电容的选择

因为输出电容是用来补偿LDO的，所以选择时必须仔细。基本上所有的LDO应用中引起的振荡都是因为输出电容的ESR过高或过低。电容器类型的选择很重要。最合适的电容器是钽电解电容器（除了一些专门设计使用陶瓷电容的LDO，例如：LP2985），尽管具有大容量的钽电解电容器尺寸很大。铝电解电容器的尺寸很小，但其ESR在低温时会变差，并且在－30℃以下无法正常工作。多层陶瓷电容器类型无法为普通的LDO提供足够的电容。测试一个AVX的4.7uF的钽电容可知它在25℃时ESR为1.3Ω，该值处在稳定范围的中心（如图4.13）。 另一点非常重要，AVX电容的ESR在－40℃到＋125℃温度范围内的变化小于2:1。铝电解电容在低温时的ESR会变大很多，所以不适合作LDO的输出电容。 必须注意大的陶瓷电容（≥1uF）通常会用很低的ESR（＜20mΩ），这几乎会使所有的LDO产生振荡（除了明确指出可以用陶瓷电容做输出匹配的）。如果使用陶瓷电容就要串联电阻以增加ESR。大的陶瓷电容的温度特性很差（通常是Z5U的），也就是说在工作范围内的温度的上升和下降会使容值成倍的变化。

4.5.3准LDO的补偿

在考虑准LDO（如图3.6）的稳定性和补偿的问题时，首先考虑到它兼有LDO和NPN稳压器的特性。因为准LDO利用NPN调整管，它的共集电极组合也就使它的输出极（射极）看上去有相对低的阻抗。 然而，由于NPN的基极是由高阻抗PNP电流源驱动的，所以准LDO的输出阻抗不会达到使用NPN达林顿管的NPN稳压器的输出阻抗那样低。（但是它比真正的LDO的输出阻抗要低）。 也就是说准LDO的功率极点的频率比NPN稳压器的低，因此准LDO也需要一些补偿以达到稳定。当然了这个功率极点的频率要比LDO的频率高很多，因此准LDO需要更小的电容而且对ESR的要求也不很苛刻。 例如，准LDO LM1085可以输出高达3A的负载电流却只需10uF的钽输出电容来确保稳定性。而且并未提供ESR图，因为在此LDO应用中对电容的ESR要求很宽松。

4.5.4要求低ESR的特定LDO

随着陶瓷电容工艺发展，容量可以做的越来越大，而便携设备对电路面积小型化要求越来越高，许多厂家推出的LDO的输出电容可以使用陶瓷电容之类的具有超低ESR的电容。例如国半的LP2985和LP2989，使用的电容的ESR可以低到5-10mΩ。通常这样小的ESR会使普通的LDO引起振荡。

为了使LDO在使用如此低的ESR时仍能够稳定工作，厂家已经在芯片内部通过使用内置零点代替了先前的钽电容的ESR零点。这样做是为了将稳定的ESR取值的上限降低。未在内部添加零点的典型LDO的稳定ESR的范围一般为100mΩ到5Ω（只适合使用钽电容并不适合使用陶瓷电容）。内置零点的稳定范围是3mΩ到500mΩ因此它可以使用陶瓷电容。

要弄清稳定范围上限下降的原因请参考图4.12。正如以上所提到的，此LDO零点被集成在内部。因此外部电容产生的零点必须处在足够高的频率，这样就不能使带宽很宽。否则，高频极点会产生很大的相移从而导致振荡。

5.1输出电压(Output Voltage)

输出电压是低压差线性稳压器最重要的参数，也是电子设备设计者选用稳压器时首先应考虑的参数。低压差线性稳压器有固定输出电压和可调输出电压两种类型。固定输出电压稳压器使用比较方便，而且由于输出电压是经过厂家精密调整的，所以稳压器精度很高。但是其设定的输出电压数值均为常用电压值，不可能满足所有的应用要求，但是外接元件数值的变化将影响稳定精度。

5.2最大输出电流(Maximum Output Current)

由于线性稳压器的调整管相当于一个电阻，电流流过电阻时会发热，因此LDO最大输出电流主要取决于它调整管的节点温度，封装材料的热阻以及工作的环境温度。一般器件手册上都会给出最大输出电流的参数。关于电流计算，可以参考后文5.11功耗和节点温度。

用电设备的功率不同，要求稳压器输出的最大电流也不相同。通常，输出电流越大的稳压器成本越高。为了降低成本，在多只稳压器组成的供电系统中，应根据各部分所需的电流值选择适当的稳压器。

5.3压降(Dropout Voltage)

压降也叫输入输出电压差，是低压差线性稳压器最重要的参数。当输入电压下降到一定程度时输出电压将不再维持在一个恒定的电压。该点发生在输入电压不断接近输出电压时。在保证输出电压稳定的条件下，该电压压差越低，线性稳压器的性能就越好。

图5.1是一个典型的LDO电路，在非调整区域PMOS可以看作一个电阻，电压降下量可以标示为：

Vdropout=Io*Ron

图 5.1

下图是TPS76733的输入输出特性，输出1A的时候它的压降是350mV，从输入电压是3.65V的时候输出电压就开始下降，从2V到3.65V是该LDO的非调整区域。输入电压如果低于2V将不会有输出，也就是说LDO不工作。比较低的电压降有利于提高LDO效率。

图 5.2 一款3.3V LDO输出电压降图

5.4接地电流(Ground Pin Current)

接地电路IGND也称为静态电流，定义为暑促电流与输入电流的差。图5.3定义了静态电流Iq=Ii-Io。通常较理想的低压差稳压器的接地电流很小。

图5.3 LDO的静态电流

静态电流由调整管的偏置电流（比如说参考电压消耗电流，采样电阻消耗电流，误差放大器消耗电流）和驱动调整管基极的电流组成。它的大小主要由调整管，LDO的结构和环境温度决定。

对于双极型晶体管，静态电流随着负载电流成比例的增加，因为双极型晶体管是电流驱动器件。另外在非调整区域，由于发射极和基极寄生电流路径的影响静态电流也会增加，该寄生电流路径是由于基极电压比输出电压低所引起的。

对于MOS管，静态电流几乎不随负载的变化而变化，几乎是一个恒定值，因为MOS管是电压驱动器件。对采用MOS管的LDO来说，对静态电流有贡献的只有参考电压的消耗，采样电阻消耗电流，误差放大器消耗电流。因此在应用中如果对静态电流的消耗比较苛刻的话，最好采用MOS管作为调整管的LDO。

5.5负载调整率(Load Regulation)

负载调整率是表征LDO抑制负载干扰能力的指标，直接反应了负载变化对输出电压的影响。可以通过图5.4和式5-1来定义：

图5.4 输出电压&电流曲线

式5-1

式中

△Vload—负载调整率

Imax—LDO最大输出电流

Vt—输出电流为Imax时，LDO的输出电压

Vo—输出电流为0.1mA时，LDO的输出电压

△V—负载电流分别为0.1mA和Imax时的输出电压之差

LDO的负载调整率越小，说明LDO抑制负载干扰的能力越强。

提高开环增益有注意改善负载调整率。

5.6线性调整率(Line Regulation)

线性调整率是表征LDO抑制输入电压变化干扰能力的指标，直接表明了输入电压对输出电压稳定性的影响。可以通过图5.5和式5-2来定义，LDO的线性调整率越小，输入电压变化对输出电压影响越小，LDO的性能越好。

图5.5 LDO输出电压&输入电压曲线

式5-2

式中

△Vline—LDO线性调整率

Vo—LDO名义输出电压

Vmax—LDO最大输入电压

△V—LDO输入Vo到Vmax'输出电压最大值和最小值之差 。

增加LDO的开环增益有助于提高线性调整率。

5.7效率

LDO的效率与输入输出电压，静态电流有关，计算公式如下：

为了尽可能提高效率，必须使压降和静态电流尽可能小。另外输入和输出电压之间的差也应该尽可能小，因为LDO的。如果不考虑负载的话，输入和输出电压的差是决定效率的一个至关重要的参数。

5.8瞬态响应

瞬态响应被定义为在输出阶跃电流条件下，输出电压的最大允许变化量。

瞬态响应通常与输出电容大小，等效ESR，旁路电容，最大允许负载电流大小有关。

瞬态电压的变化量可以定义为

Δt1与LDO闭环带宽有关，ΔVESR是由于输出电容的ESR导致的变化量的大小，实际应用决定了这个值应该多小。

图5.6是一个1.2V LDO的瞬态响应过程，输出电容的大小为4.7uF，瞬间负载吸收将近90mA的电流，电压最大的下降量为120mV。随后在1us的时间里LDO控制环路对负载电流的变化做出响应（Δt1=1us）,LDO的带宽决定了Δt1大小，最后17us之内输出电压达到稳定状态。

为了获得更好的瞬态响应，LDO需要更宽的带宽，更大的输出容量，低ESR电容（当然要满足最小ESR要求）

5.9纹波抑制比

电源噪声抑制比也叫纹波抑制比。是衡量LDO对输入电压电源变动抑制的一种能力，与线性调整率不同的一点是，纹波抑制比需要考虑很宽的频率范围。

图5.7 纹波抑制比

纹波抑制比的定义：

举个例子，频带为100kHz范围内的文博抑制对于DC/DC电源给线性电源供电的结构来说非常重要，因为DC/DC电源纹波频率正好在这个范围之内。图5.7所示的100kHz到1MHz范围内的LDO的纹波抑制比就不怎么好。

控制环路往往是决定纹波抑制比的主要因素，大的输出电容，低ESR，追加旁路电容能够改善纹波抑制比。

5.10 精度

考虑到LDO线性调整率，负载调整率，参考电压漂移，误差放大器电压漂移，外部取样电阻的精度，温度细说等综合参数的总体影响，有了精度这个概念。

对于LDO输出电压变化影响最大的是温度。因为参考电压和误差放大器对温度的变化比较敏感。其次是电阻的精度。线性调整率，负载调整率，增益误差对精度的影响只有1%到3%。

5.11 功耗和节点温度

大多数的LDO为了确保能够正常动作都会指定它的最大节点温度。最大节点温度范围之内，LDO不会损坏。

线性电压调整器在工作时承载的功耗极限由器件结点(Junction)极限温度决定 。功耗由两部分组成:

(1) 输出电流乘以输入输出电压差 (Iout)(Vin-Vout)；

(2) GND引脚电流乘以输入电压 (IGND )(Vin) 。

功耗产生热的温度不能超过结点温度极限(125℃) 。

为了保证节点温度不至于过高，LDO的功耗必须限定在一定的范围之内。有必要计算最大允许功耗Pdmax和实际功耗Pd。很显然Pd必须小于等于Pdmax。

LDO最大热耗计算公式：

这里，Tjmax为节点最高温度

TA为环境温度

RΘja为节点温度到环境温度的热阻

LDO功耗计算公式：

以LT1764EQ为例， 假定输出电压3.3V，输入电压范围46V，输出电流0500mA，最大环境温度为50℃，则计算最大结点温度为:

IOUT(MAX)(VIN(MAX) - VOUT) + IGND(VIN(MAX))

这里:

IOUT(MAX) = 500mA； VIN(MAX) = 6V； IGND at (IOUT = 500mA， VIN = 6V)= 10mA

于是:

P = 500mA(6V - 3.3V) + 10mA(6V) = 1.41W

DD封装的热阻根据敷铜面积不同取23℃/W~33℃/W， 因此结点温升大约为:

1.41W(28℃/W) = 39.5℃

结点最大温度为: TJMAX = 50℃ + 39.5℃ = 89.5℃< 125℃

因此，此设计是合理的。当然目前许多线性稳压器都具有自保护特征，如过流保护，过热保护等。