麦克斯韦方程组中散度和旋度的物理意义

麦克斯韦方程组是一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。它由四个方程组成：描述电荷如何产生电场的高斯定律、论述磁单极子不存在的高斯磁定律、描述电流和时变电场怎样产生磁场的麦克斯韦-安培定律、描述时变磁场如何产生电场的法拉第感应定律。四个方程中，两个方程涉及到散度，另外两个方程涉及到旋度。散度和旋度是对向量场进行微分运算的两种方式，它们可以用来刻画向量场的性质。那么，散度和旋度具体有什么物理意义呢？

散度

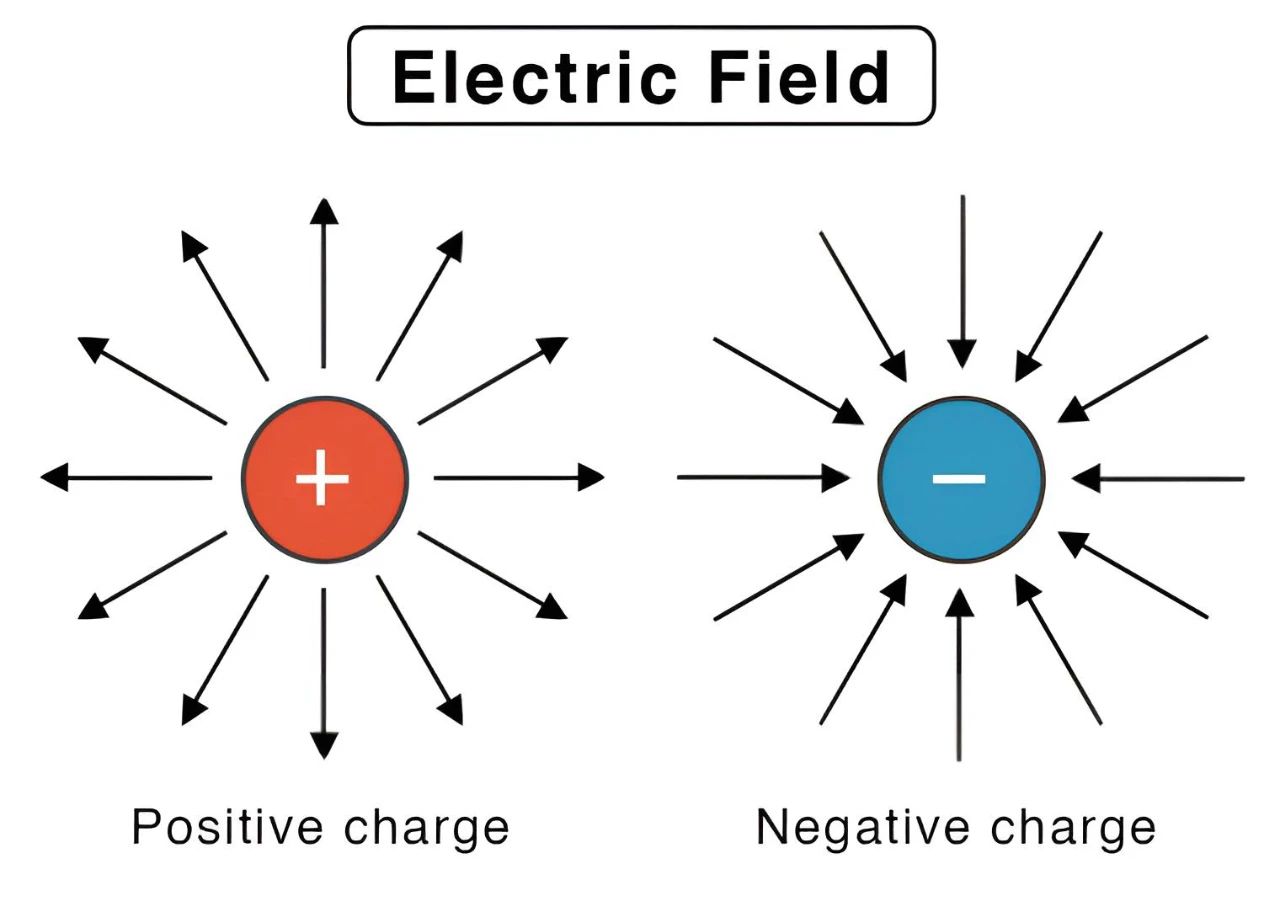
散度是一个标量，它表示一个向量场在某一点处的发散程度。如果一个向量场在某一点处的散度为正，那么说明该点附近有向量从内部向外部发散；如果为负，那么说明有向量从外部向内部汇聚；如果为零，那么说明该点附近向量场没有发散或收敛的趋势。散度的物理意义是，如果在一个向量场中取一个小闭合曲面，那么该曲面上的向量通量与曲面包围的体积成正比。

在麦克斯韦方程组中，高斯定律和高斯磁定律都涉及到了散度。高斯定律可以表示成如下形式：∇⋅E=ρ/ε_0。其中∇·表示散度运算，E表示电场强度，ρ表示电荷密度，ε_0表示真空中的介电常数。这个方程告诉我们，电场在某一点处的散度等于该点处单位体积内的净电荷除以真空介电常数。也就是说，电荷是产生电场散度的源头。如果某一点处有正电荷，那么该点处的电场散度为正，说明有电场线从该点向外发散；如果有负电荷，那么该点处的电场散度为负，说明有电场线从外部向该点汇聚；如果没有净电荷，那么该点处的电场散度为零，说明该点附近电场没有发散或收敛的趋势。

另一方面，高斯磁定律可以写成如下的微分形式：∇⋅B=0。其中B表示磁场强度。这个方程告诉我们，磁场在某一点处的散度等于零，也就是说，该点附近没有磁荷或磁单极子。如果某一点处有磁荷，那么该点处的磁场散度不为零，说明有磁场线从该点向外发散或从外部向该点收敛。但是，目前还没有发现任何证据表明磁单极子的存在，因此高斯磁定律是一个普遍成立的定律。

旋度

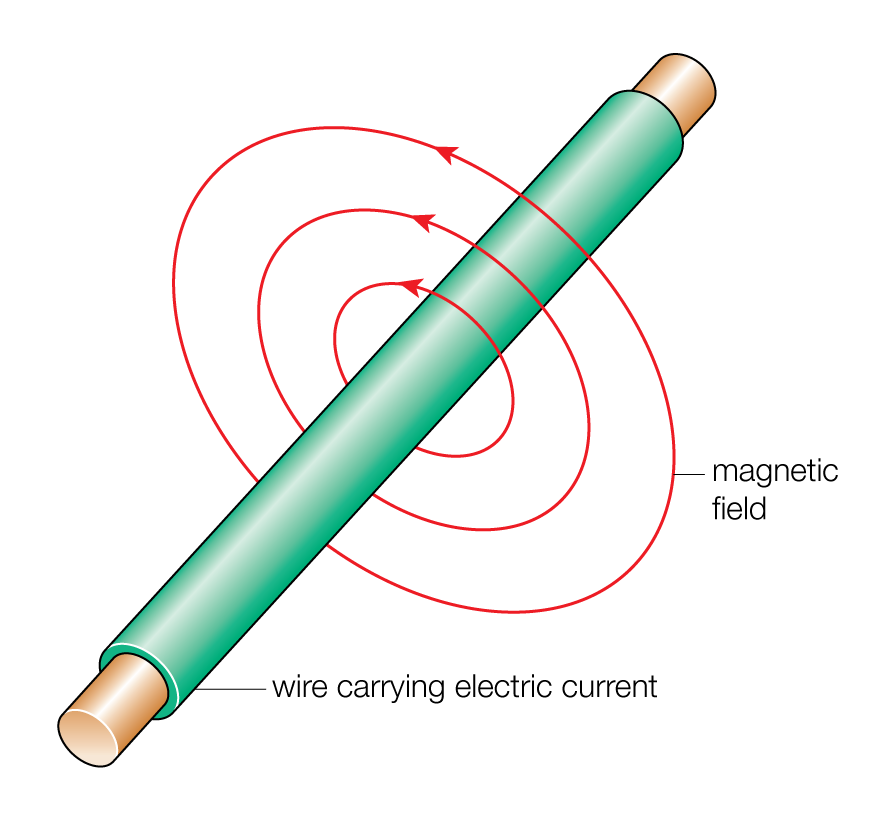
旋度是一个向量，它表示一个向量场在某一点处的旋转程度。旋度的物理意义是，如果在一个向量场中取一个小闭合回路，那么该回路上的向量环流与回路包围的面积成正比。旋度的方向由右手定则确定，即如果右手四指沿着回路方向弯曲，那么大拇指指向的方向就是旋度的方向。如果旋度不为零，表示向量场在该点有旋转性；如果旋度为零，表示向量场在该点无旋转性。法拉第感应定律可以写成∇×E=−∂B/∂t，其中∇×表示旋度运算。它告诉我们，当一个闭合回路在一个变化的磁场中时，会在回路上感应出一个电动势，从而产生电流。这个电动势的大小等于回路包围的面积内磁通量的变化率的负值。

从公式可以看出，感应电场是一个旋转性的场，它的旋度方向垂直于磁通量的变化方向。这样，我们就可以用右手定则来判断感应电流的方向：如果右手大拇指指向磁通量增加的方向，那么右手四指弯曲的方向就是感应电流的方向。同样地，麦克斯韦-安培定律可以表示为：∇×B=μ_0（J+ε_0∂E/∂t），它告诉我们，当一个闭合回路在一个变化的电场中时，会在回路上产生一个磁动势，从而形成磁场。从公式我们可以看出，产生磁场的原因有两个：一是电流，二是变化的电场。这两个因素都会使得磁场具有旋转性，它们的旋度方向垂直于电流或电场矢量的变化方向。这样，我们也可以用右手定则来判断磁场线的方向：如果右手四指指向电流或电位移矢量增加的方向，那么右手大拇指指向的方向就是磁场线的方向。

通过以上分析，我们可以发现，散度和旋度是描述电磁场分布和变化的两个重要工具。散度反映了电荷或磁单极子（如果存在）对电场或磁场的影响；旋度反映了时变电场或时变磁场对彼此产生影响的方式。麦克斯韦方程组用散度和旋度将四个基本定律统一起来，揭示了电磁现象背后的普遍规律。

编辑：黄飞