聊聊关于PWM调控模式

PWM的全称是脉冲宽度调制(Pulse-width modulation)，是通过将有效的电信号分散成离散形式从而来降低电信号所传递的平均功率的一种方式；

PWM一种模拟控制方式，根据相应载荷的变化来调制晶体管栅极或基极的偏置，来实现开关稳压电源输出晶体管或晶体管导通时间的改变，这种方式能使电源的输出电压在工作条件变化时保持恒定。脉冲宽度调制(PWM )是一种对模拟信号电平进行数字编码的方法。

通过高分辨率计数器的使用，方波的占空比被调制用来对一个具体模拟信号的电平进行编码。PWM信号仍然是数字的，因为在给定的任何时刻，满幅值的直流供电要么完全有(ON)，要么完全无(OFF)。电压或电流源是以一种通(ON)或断(OFF)的重复脉冲序列被加到模拟负载上去的。

通的时候即是直流供电被加到负载上的时候，断的时候即是供电被断开的时候。只要带宽足够，任何模拟值都可以使用PWM进行编码。

采样控制理论中有一个重要结论：冲量相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同.PWM控制技术就是以该结论为理论基础，对半导体开关器件的导通和关断进行控制，使输出端得到一系列幅值相等而宽度不相等的脉冲，用这些脉冲来代替正弦波或其他所需要的波形。所以根据面积等效法则，可以通过对改变脉冲的时间宽度，来等效的获得所需要合成的相应幅值和频率的波形.

按一定的规则对各脉冲的宽度进行调制，既可改变逆变电路输出电压的大小，也可改变输出频率。PWM控制的基本原理很早就已经提出，但是受电力电子器件发展水平的制约，在上世纪80年代以前一直未能实现。直到进入上世纪80年代，随着全控型电力电子器件的出现和迅速发展，PWM控制技术才真正得到应用。

PWM实现的原理是通过锯齿波/三角波(载波)所需要合成的波形(调制波)进行比较，然后确定PWM所需要输出的极性，通常是ON或者是OFF，因为一般都是作用到开关元器件上；如下图所示；

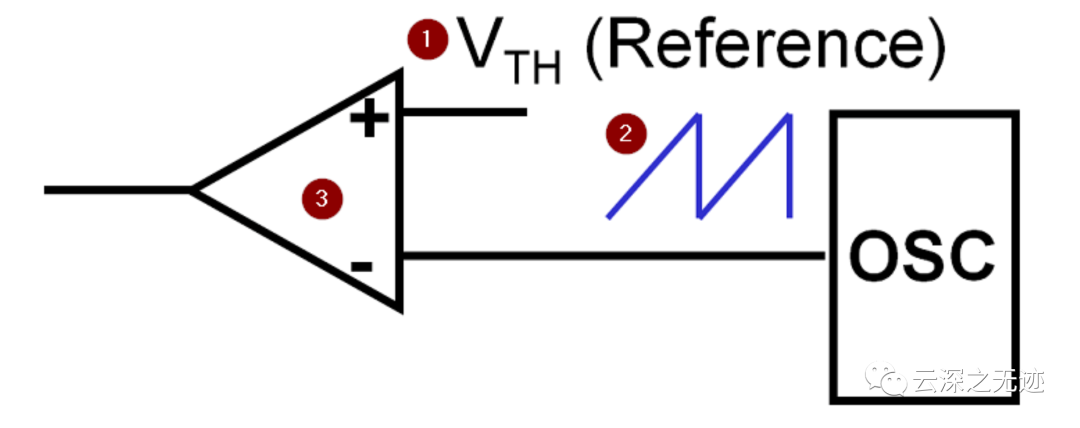
用Siumlink模拟一下

振荡器输出的锯齿波和参考值 进行比较，然后就可以输出PWM波形了；

50%的占空比

1.锯齿波(图中橙色波形)最大为10，然后我希望输出平均为5的波形(图1中红色的水平直线)；

2.那么通过比较，当锯齿波小于5时；PWM输出低电平，即为OFF；

3.当锯齿波大于5时，PWM输出高电平，即为ON；

参考STM32中PWM的配置，根据载波波形的形状，假设三角波最大值是10，那么它的变化过程可能存在以下两种情况：

1.完整周期包括两个过程，先递增，再递减：增加增加减少减少，这种也叫中央对齐PWM；

2.完整周期只有递增过程：增加增加；

脉冲波的中心将会被固定在时间窗格的中心，同时脉冲波的两边可以移动，使得波的宽度被延伸或压缩，具体如下图所示；

中央对齐的PWM模式

这个是另外一种的输出

电流控制PWM的基本思想是把希望输出的电流波形作为指令信号，把实际的电流波形作为反馈信号，通过两者瞬时值的比较来决定各开关器件的通断，使实际输出随指令信号的改变而改变。

空间电压矢量控制PWM(SVPWM)也叫磁通正弦PWM法。它以三相波形整体生成效果为前提，以逼近电机气隙的理想圆形旋转磁场轨迹为目的，用逆变器不同的开关模式所产生的实际磁通去逼近基准圆磁通，由它们的比较结果决定逆变器的开关形成PWM波形。此法从电动机的角度出发，把逆变器和电机看作一个整体，以内切多边形逼近圆的方式进行控制使电机获得幅值恒定的圆形磁场(正弦磁通)。具体方法又分为磁通开环式和磁通闭环式磁通开环法用两个非零矢量和一个零矢量合成一个等效的电压矢量，若采样时间足够小可合成任意电压矢量。

矢量控制也称磁场定向控制，其原理是将异步电动机在三相坐标系下的定子电流la，Ib及Ic，通过三相/二相变换，等效成两相静止坐标系下的交流电流la1及Ib1，再通过按转子磁场定向旋转变换，等效成同步旋转坐标系下的直流电流Im1及It1(Im1相当于直流电动机的励磁电流;It1相当于与转矩成正比的电枢电流)，然后模仿对直流电动机的控制方法，实现对交流电动机的控制其实质是将交流电动机等效为直流电动机分别对速度磁场两个分量进行独立控制通过控制转子磁链，然后分解定子电流而获得转矩和磁场两个分量，经坐标变换，实现正交或解耦控制。但是，由于转子磁链难以准确观测，以及矢量变换的复杂性，使得实际控制效果往往难以达到理论分析的效果，这是矢量控制技术在实践上的不足，此外。它必须直接或间接地得到转子磁链在空间上的位置才能实现定子电流解耦控制，在这种矢量控制系统中需要配置转子位置或速度传感器。这也就是为什么有那么多传感器知道位置的原因。

https://blog.csdn.net/ic2121/article/details/119883174

原文链接：https://blog.csdn.net/ic2121/article/details/119883174