

傅里叶变换与信号的频谱讲解
描述
1 信号与系统的基本概念
信号是信息和消息传播的载体和工具,一般表现为随时间不断变化的某种物理量或者物理参数。
信号:基带信号、载波信号、已调信号、噪声,……
系统是指由若干相互有联系的事物组合而成的整体,用于将送入系统的输入信号进行加工处理、运算变换后得到期望的输出信号,或者将信号传输到接收端。
系统:通信系统、发射机、接收机、信道、……
信号的分类:
模拟信号、数字信号;
连续信号、离散信号、数字信号
确定信号、随机信号——
确定信号:能够用确定的时间函数表达式或波形图描述,在任一指定时刻的幅度都可以根据函数表达式或波形图来确定。
随机信号:如果没有确定的时间函数表达式,在任一时刻的幅度取值事先都不可确定,而只知道幅度取为某个数值的概率有多大。
2 傅里叶变换与信号的频谱
2.1 信号的频谱
频谱(Spectrum)
通过傅里叶变换可以将信号分解为不同频率的正弦信号分量的叠加,而信号的傅里叶变换F(jω)反映了信号中各分量的幅度和相位随其角频率ω的变化关系。
称为信号的频谱密度。 简称为频谱(Spectrum)。
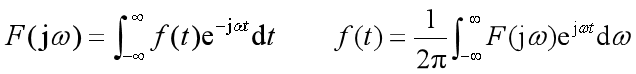
幅度谱、相位谱
对实信号,幅度谱为偶函数,相位谱为奇函数
单边谱、双边谱
能量信号的频谱
所有能量信号的频谱都不含有冲激函数,而是以ω为自变量的连续或者分段函数。
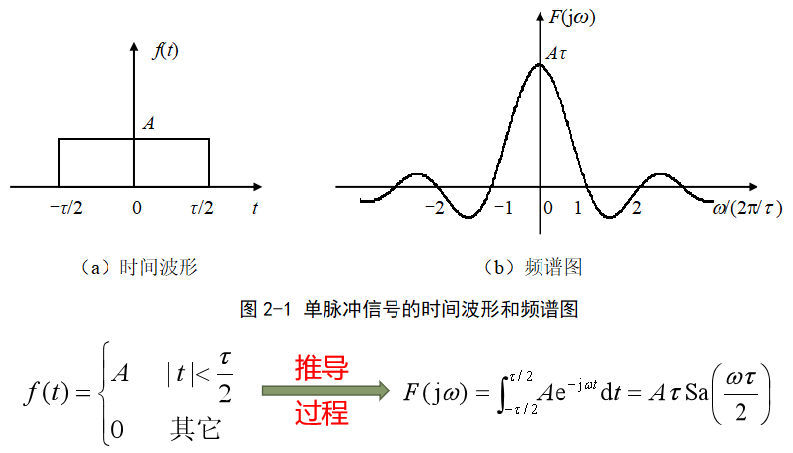
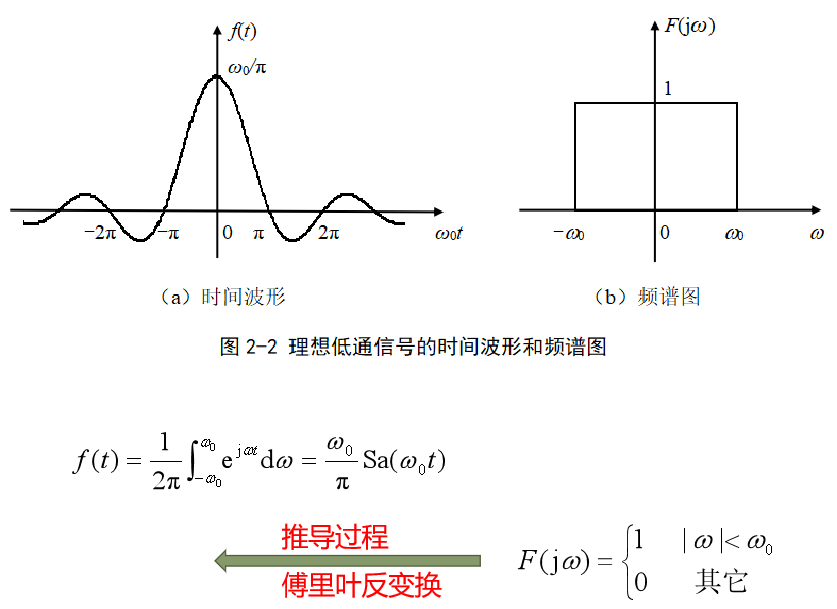
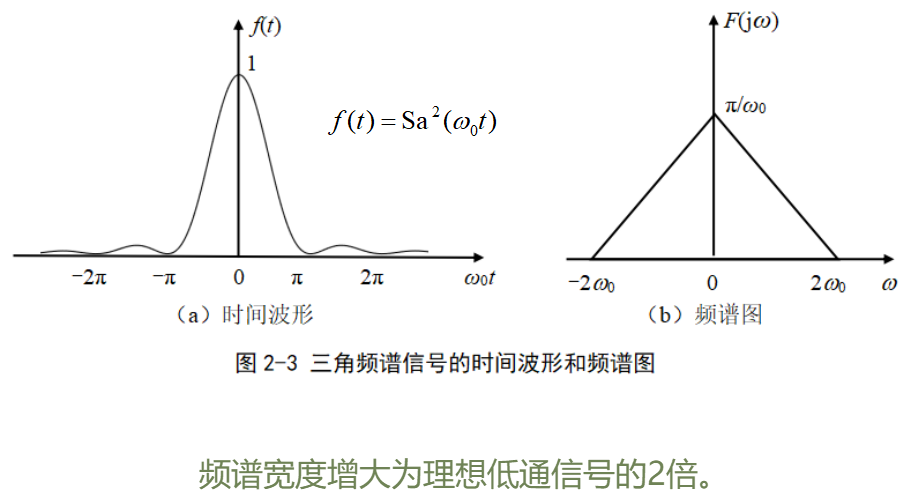
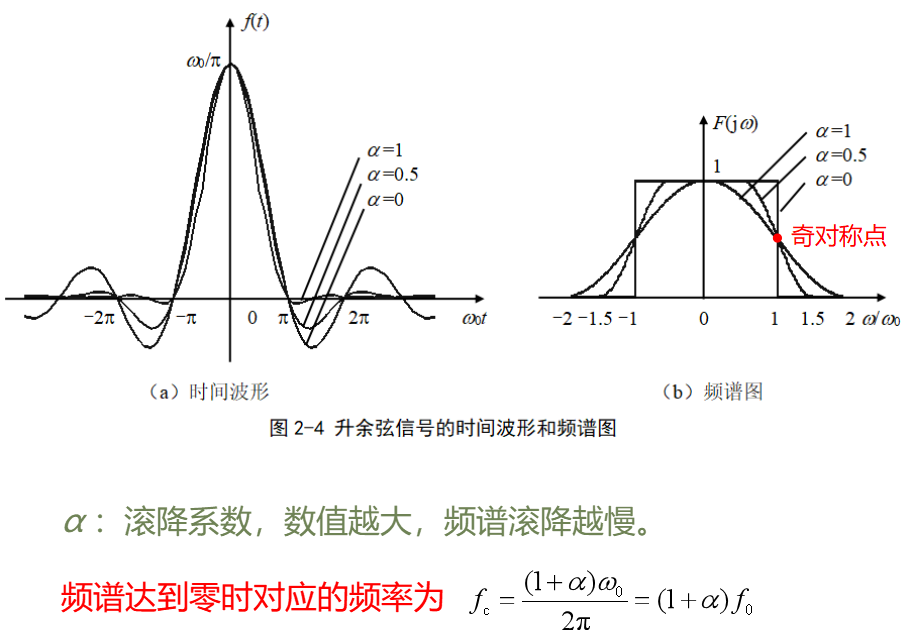
周期信号的频谱
周期信号的频谱由无穷多个冲激构成,各冲激函数位于基波角频率的整数倍位置。
因此周期信号的频谱都是离散谱,而非周期信号和能量信号的频谱都是连续谱。
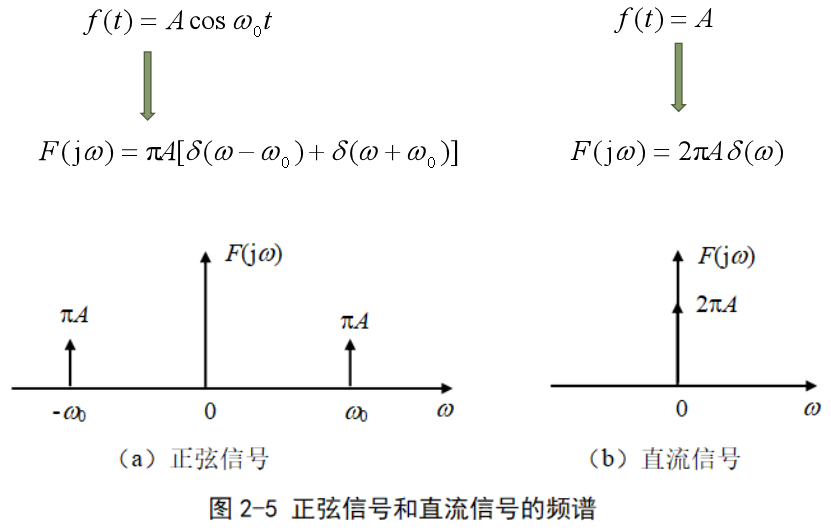
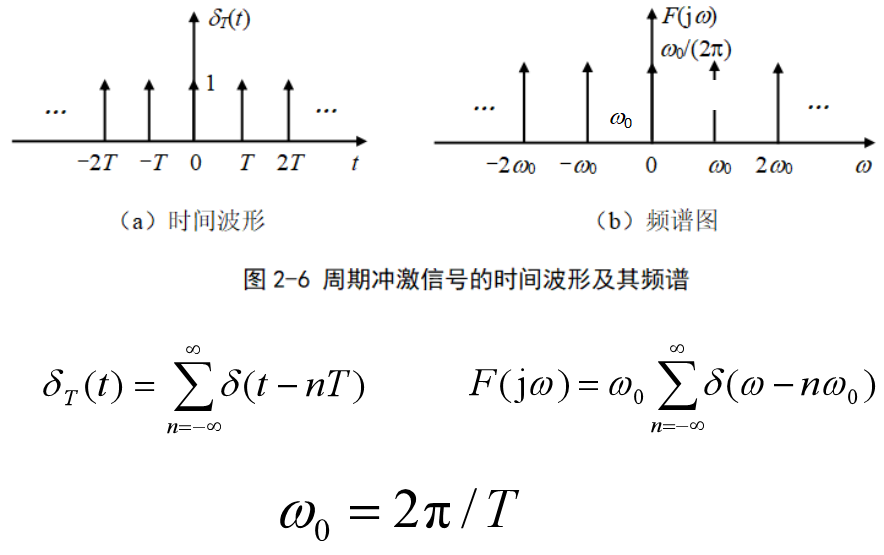
傅里叶变换的另一种形式
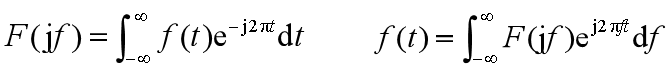
两种形式之间的关系:
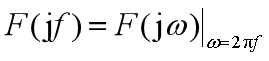
特别注意:对周期信号
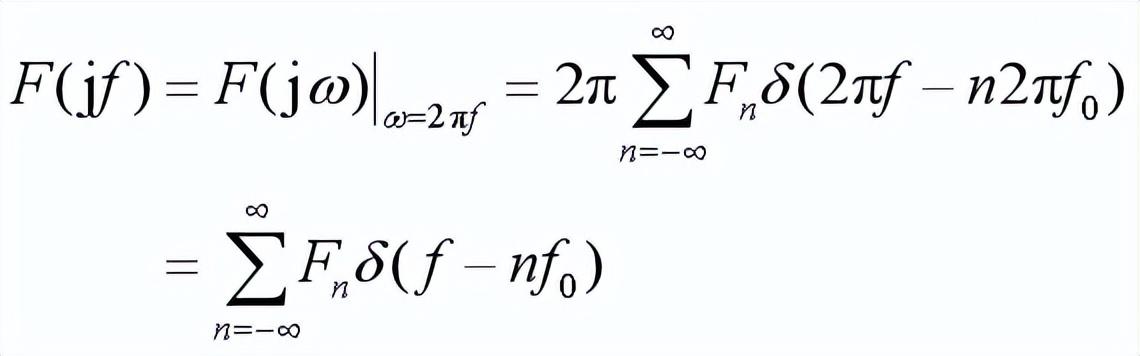
例如,周期冲激信号——
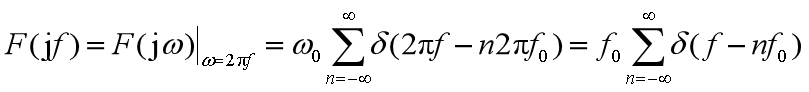
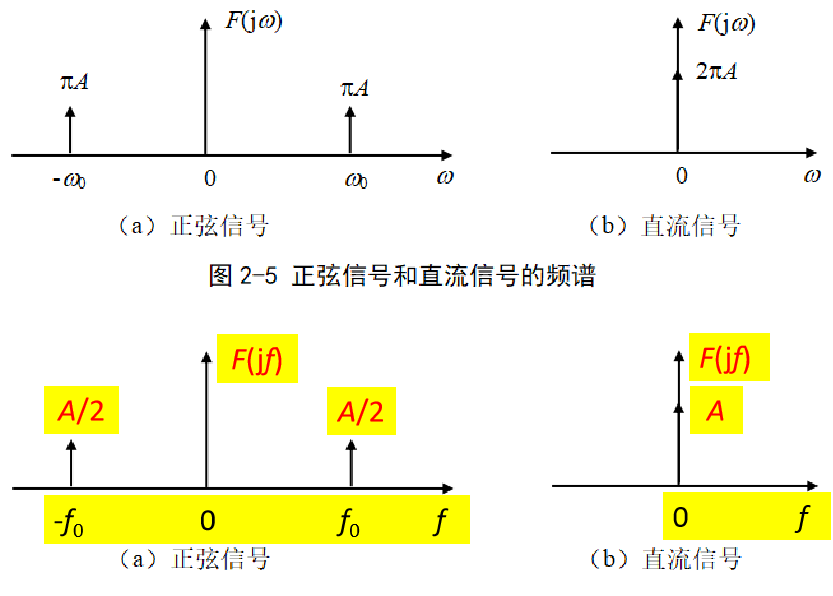
2.2 傅里叶变换的常用性质
时移性质
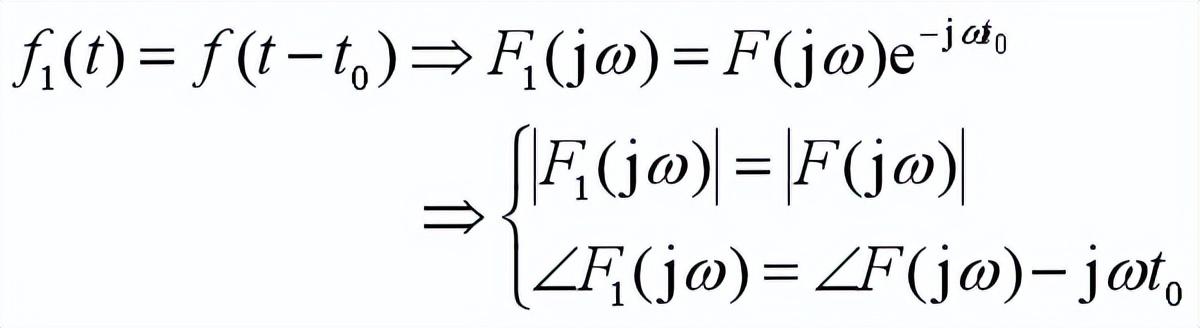
物理含义——
在时域,将信号沿着时间轴平移;
在频域,信号的幅度谱将保持不变,只是相位谱有附加的相移-ωt₀,即信号中的所有分量都将平移相同的时间t₀。
尺度变换性质
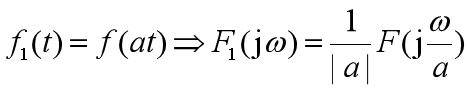
物理含义:
信号的时宽与带宽成反比。
在时域增加信号的持续时间,则信号的频谱宽度将得到压缩;
反之,减小信号持续的时间,信号的频谱宽度将增大。
在通信系统中,要求以更快地的速度传输信号,相当于将信号在时域中进行压缩,则信号的带宽将增大,也就要求传输信道提供更大的带宽。
频移性质(调制定理)
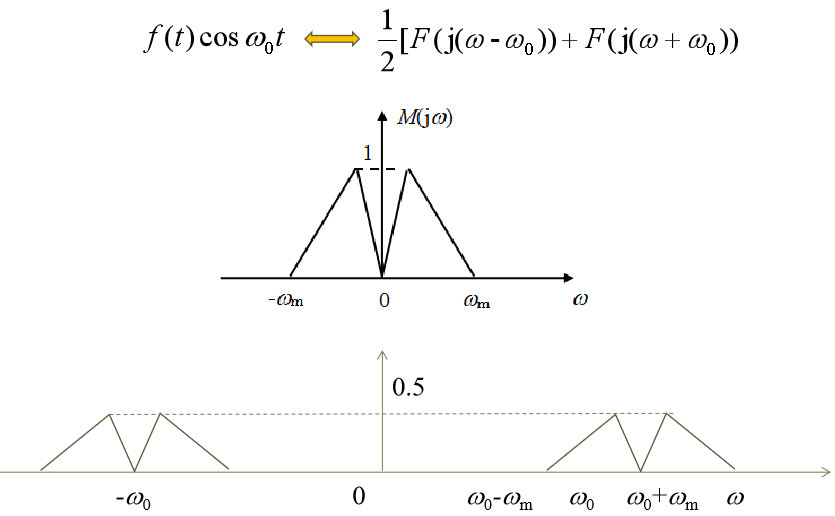
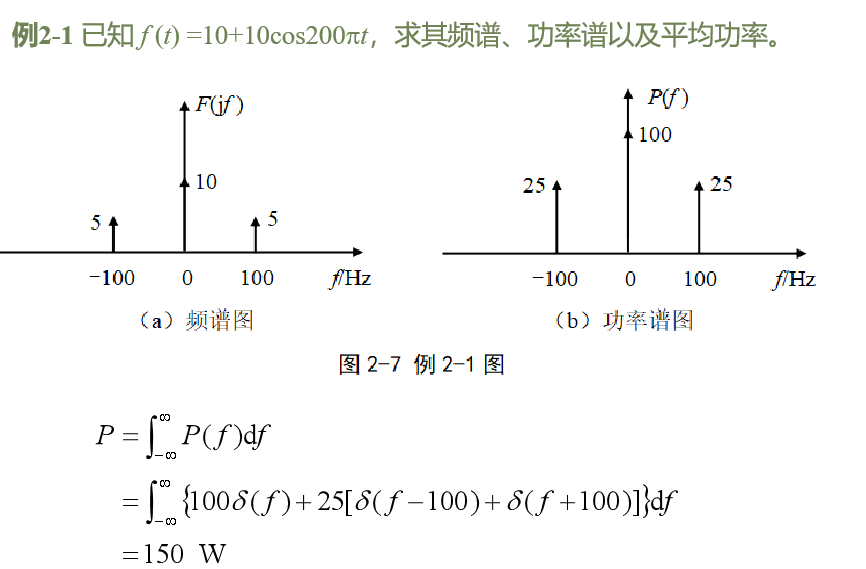
2.3 信号的能量谱、功率谱与自相关函数
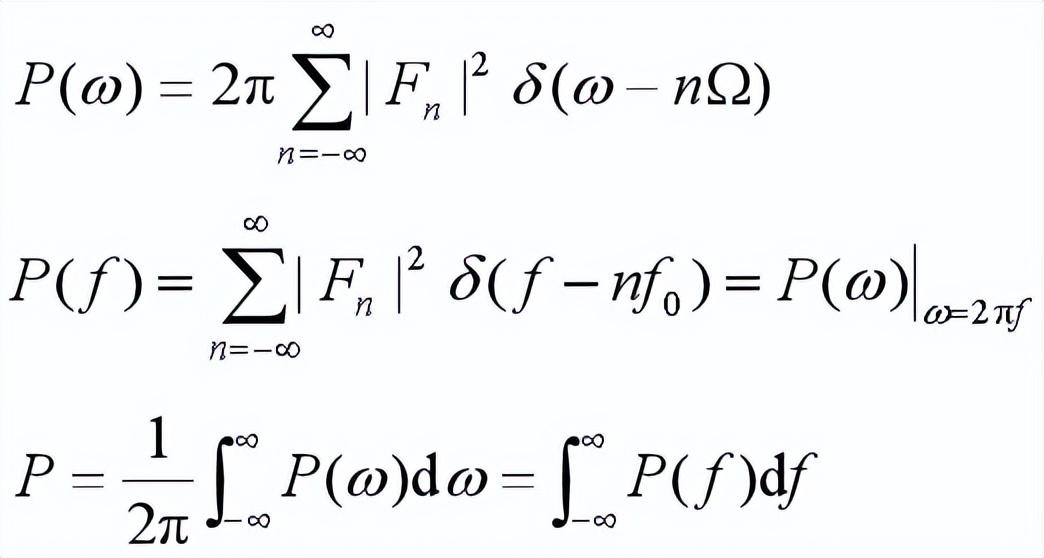
频谱代表的是信号中各频率分量的幅度和相位
功率谱代表的是信号中各分量的功率
信号的总功率等于各分量功率的和(连续和、积分)
2.4 信号的带宽
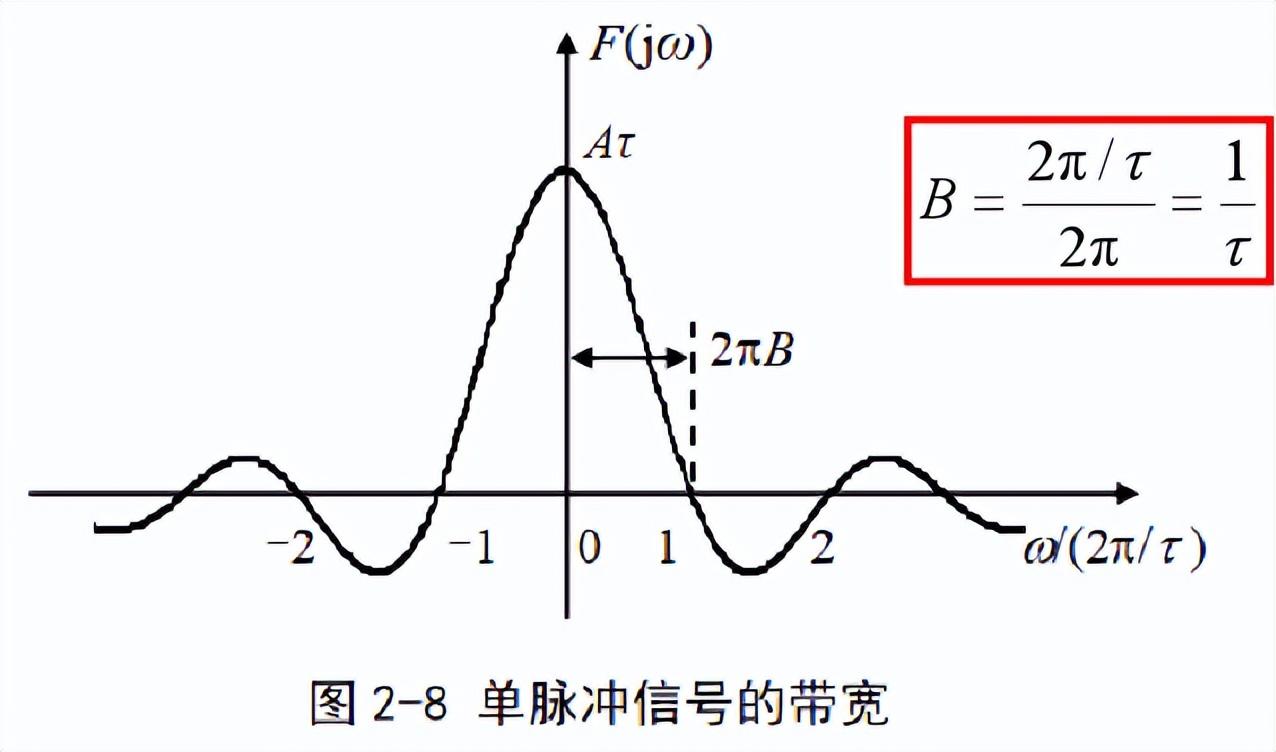
信号通过傅里叶变换分解为很多不同频率正弦信号分量的叠加,信号的频带宽度B(简称为带宽 Bandwidth)
定义为所有分量频率的变化范围,或者频谱图中右半平面不恒为0的部分在横轴上的投影宽度,单位为Hz。
近似带宽:
实际信号的频谱都具有收敛性,各分量的幅度都将随着频率的增大而逐渐衰减。
超过一定频率的分量,其幅度可以忽略,因此可将该频率近似定义为信号的带宽。
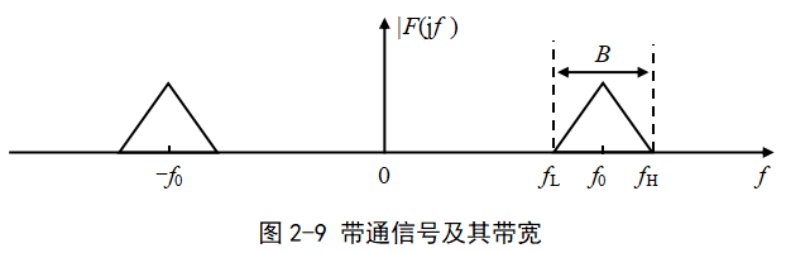
带通信号的带宽:
对通信系统中传输的各种已调信号,大都属于带通信号,也就是信号的频谱位于某个较高的频率 f₀ 附近,如图2-9所示。
一般情况下,当
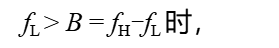
即可视为带通信号。
3 线性系统与滤波器
3.1 线性系统及其频率特性
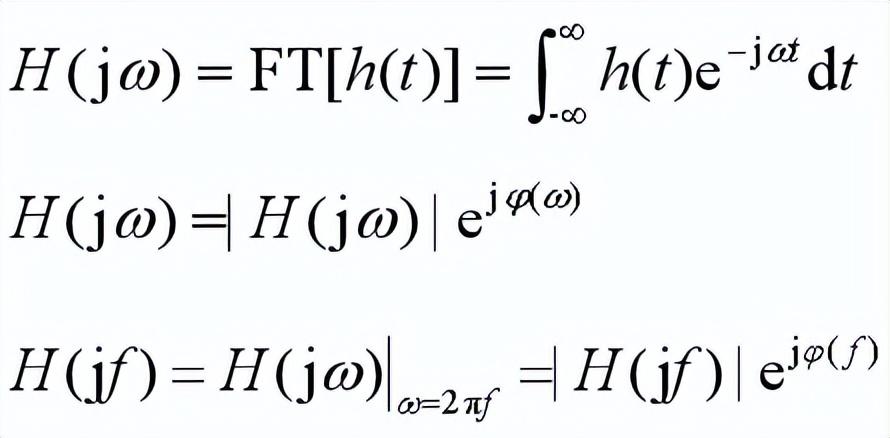
物理含义——
幅频特性| H(jω)|或| H(jf )|代表信号通过系统传输时,
系统对其中各分量幅度的放大倍数,
而相频特性φ(ω)或φ( f )代表信号中各分量相位和时间的延迟。
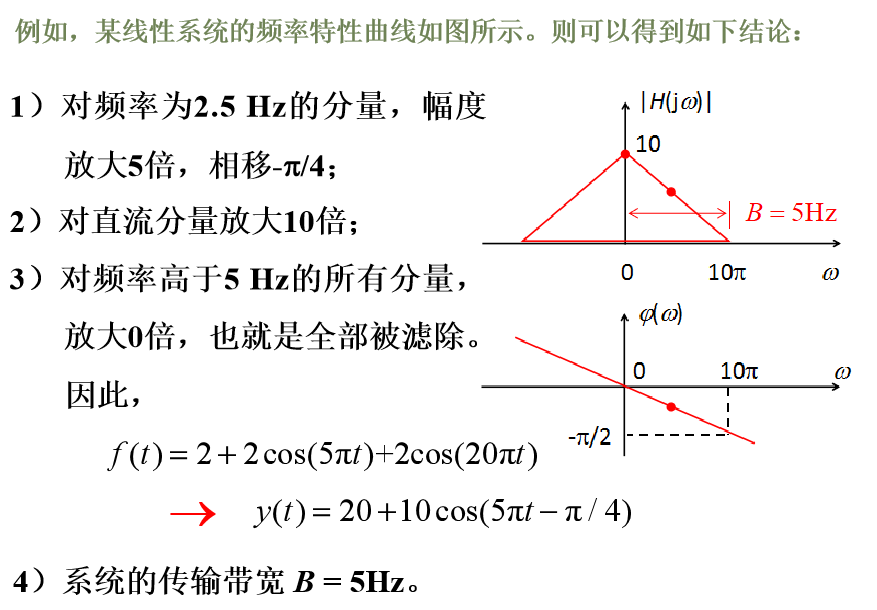
3.2 系统响应的频域求解
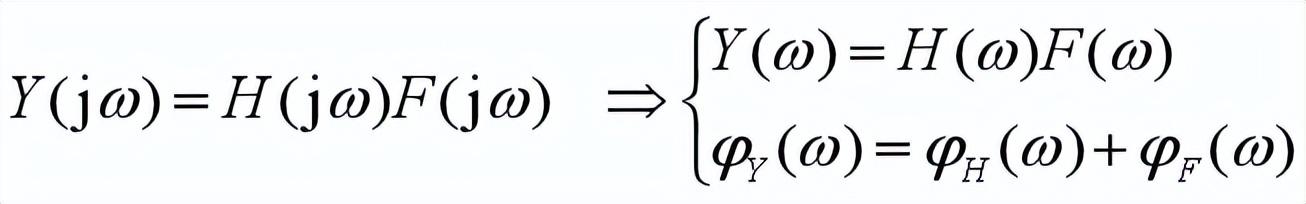
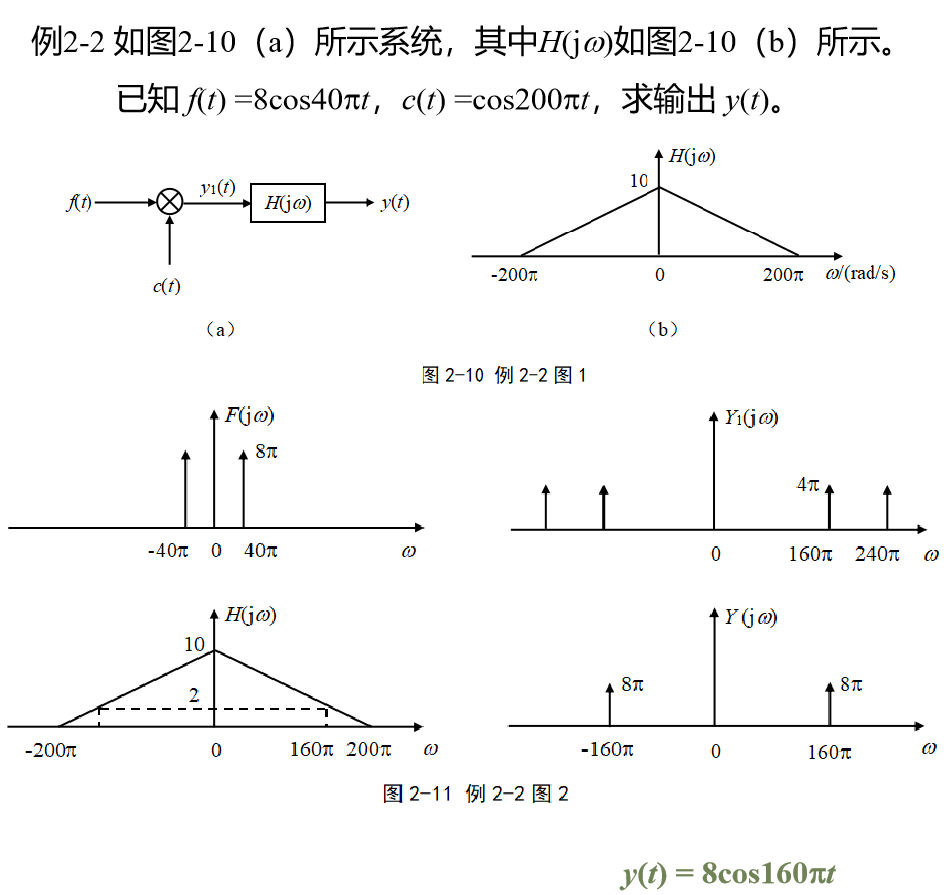
3.3 滤波器
系统的无失真传输
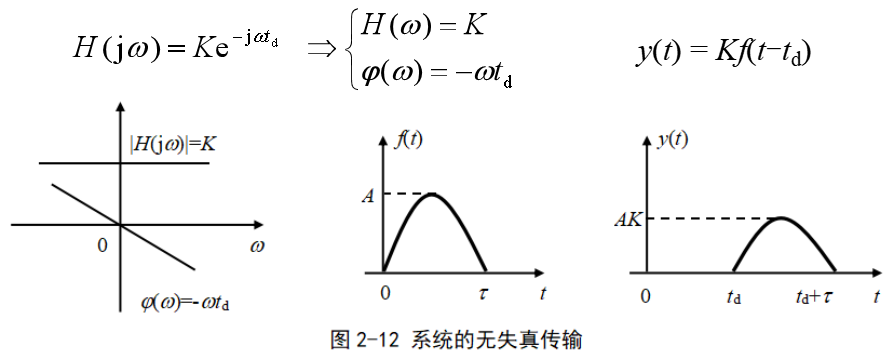
满足上述条件的系统,带宽为无穷大。
考虑到实际系统传输的信号带宽有限,只要满足系统带宽不低于传输信号的带宽,就近似认为传输没有失真。
例 数字信号通过不同带宽的信道(滤波器):
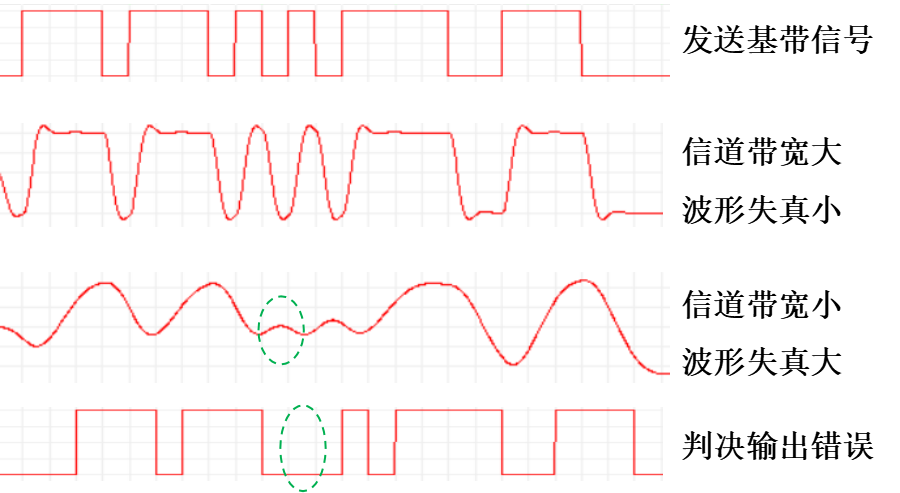
滤波器
信号通过系统时,有些分量被全部滤除,而另外一些分量能够通过系统,
在系统的输出信号中存在同频率的分量。 具有这种特性的系统称为滤波器。
根据幅频特性,将理想滤波器分为四种基本类型,即
低通滤波器(LPF,Low Pass Filter)高通滤波器(HPF)带通滤波器(BPF)带阻滤波器(BSF)
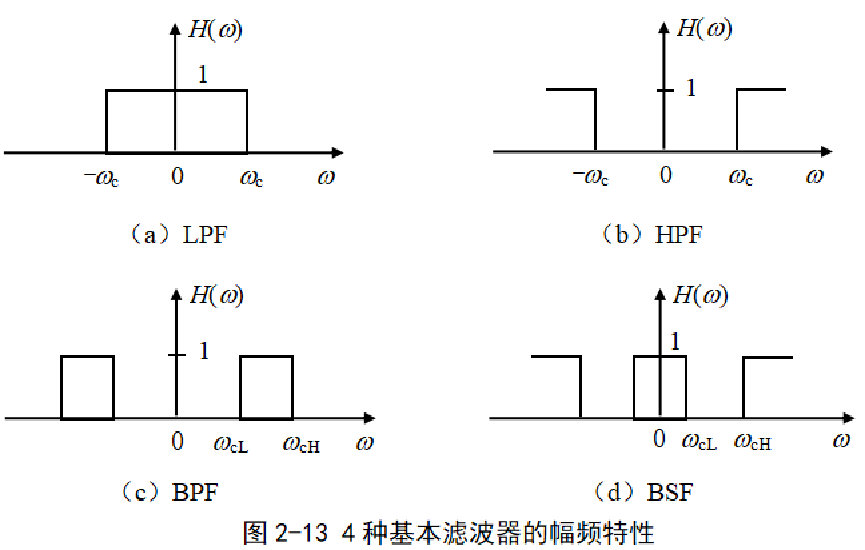
例2-3 某理想LPF的频率特性如图2-14所示。 其中
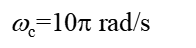
(1)求滤波器的单位冲激响应h(t)。
(2)求系统在f(t) = 5cos2πt +cos12πt作用下的输出响应y(t)。
(3)为使上述信号通过滤波器后不失真,该如何调整滤波器的参数?
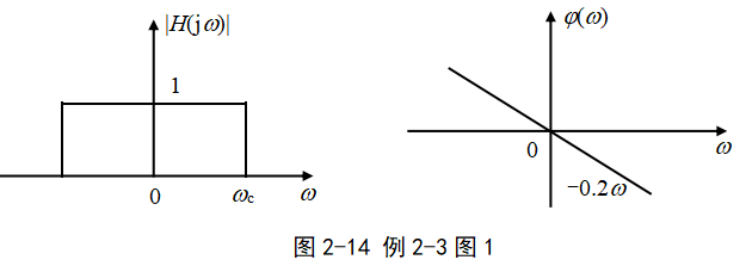
解
由于输入信号中的两个分量分别位于低通滤波器的通带和阻带内,因此只有低频分量能够通过低通滤波器,从而使得输入输出信号的波形有失真。 为避免失真,应该使输入信号中的两个分量都位于滤波器的通带内。 因此,应将滤波器的截止频率c增大,并使之满足c >12 rad/s,即滤波器的带宽至少应增大到6Hz。
希尔伯特滤波器
希尔伯特(Hilbert)滤波器是一个宽带移相网络,其幅频特性具有全通特性,相频特性对输入信号中的所有频率分量都移相-π/2。
2.4 信道及其特性
4.1 信道的分类
信道的分类
有线信道、无线信道;
模拟信道、数字信道;
调制信道、编码信道
4.2 信道的数学模型
调制信道
至少有一个输入端和一个输出端;
大多数的调制信道都是线性的,可以视为一个滤波器;
传输过程中会有延迟和衰减;
传输过程中会引入噪声,使得输入端没有信号时,信道的输出端仍会有输出噪声。
编码信道
传输过程可以认为是对数字序列的变换,即把一种数字序列变成另一种数字序列。 因此编码信道是一种数字信道。
信号传输过程中,各种噪声对编码信道的影响,最终表现为数字序列的变化。 由于干扰的存在,编码器输出数字代码序列通过信道传送到译码器时,将使得译码输出代码序列发生错误。
4.3 信道特性对传输的影响
根据乘性干扰的性质,可以将调制信道分为恒参信道和随参信道。
恒参信道的乘性干扰不随时间变化或基本不变化,
随参信道的乘性干扰是随机变化的。
典型的恒参信道包括有线信道和部分无线信道。
由信道幅频特性不理想而造成的失真称为幅频失真。如果用这种信道传输数字信号,将会引起相邻码元波形在时间上的相互重叠,造成码间干扰。如果信道不具有理想的群延迟特性,将使得信号中的各分量有不同的延迟,从而引起合成波形发生畸变。这种由信道相频特性不理想造成的失真称为相频失真。
5 噪声
5.1 噪声的来源及分类
噪声的来源及分类
根据对信号产生作用和影响的方式,噪声可以分为加性噪声和乘性噪声。
乘性噪声对信号的影响是以相乘的形式出现,而加性噪声与信号呈叠加关系。
通过对通信系统的精心设计,有些噪声可以消除或者得到衰减。但仍有一些噪声由于无法确切地预测其波形,所以无法消除其对有用信号传输的影响。这种不能预测的噪声统称为随机噪声。
随机噪声主要有热噪声、散弹噪声以及宇宙噪声等。这类噪声大多属于加性噪声。
5.2 高斯噪声和白噪声
高斯噪声
高斯噪声在每个时刻的幅度瞬时值服从高斯分布,幅度概率密度函数可表示为:

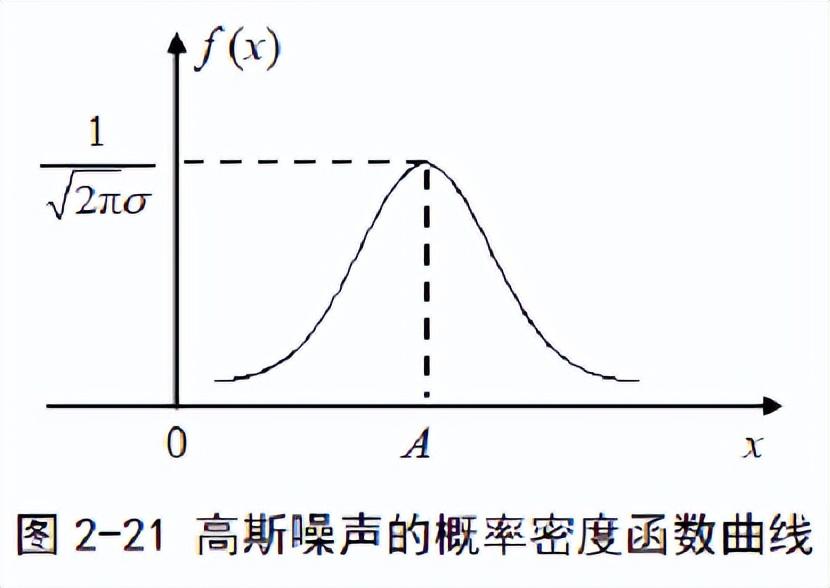
白噪声与带限白噪声
白噪声的功率谱在整个频率范围为常数,即
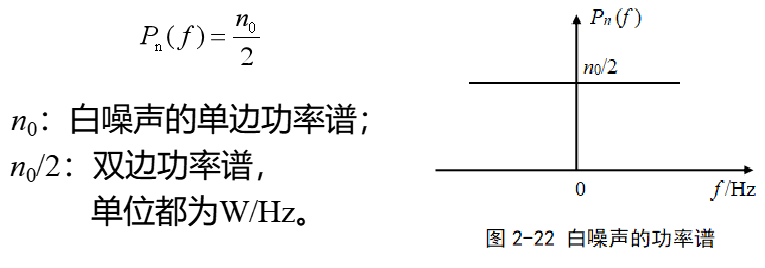
白噪声通过带宽有限的通信系统或滤波器后,频带将受到限制,这种白噪声称为带限白噪声。
根据系统和滤波器特性的不同,典型的带限白噪声又分为低通型和带通型两种。
5.3 窄带高斯白噪声
时域和频域特性
带宽远小于中心频率(B << f0);
幅度服从高斯分布;
功率谱密度在带宽范围内为常数,而在带外为0。
由于同相分量和正交分量具有相同的功率谱,因此其平均功率相同,即
窄带高斯白噪声与正弦波的叠加

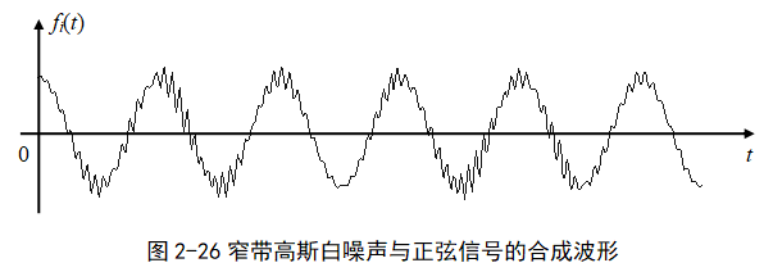
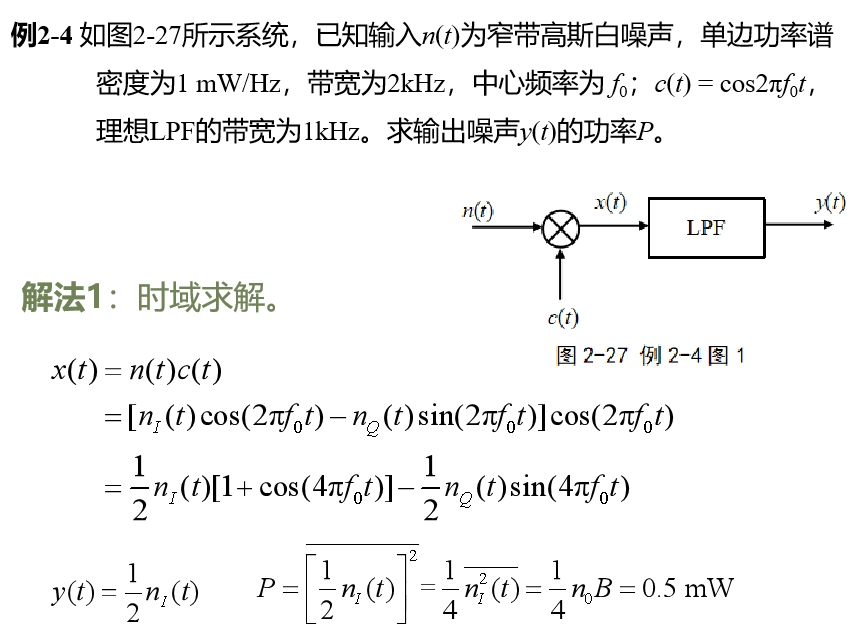
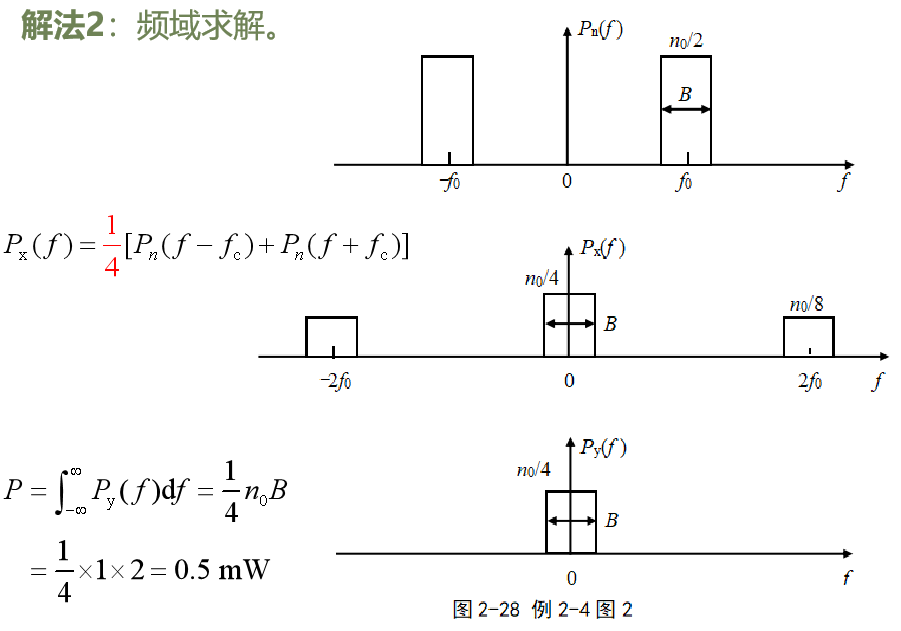
-
傅里叶变换在信号处理中的应用2024-11-14 6469
-
什么是实时频谱分析仪呢?傅里叶变换(FFT)如何实现频谱测量?2024-01-19 4646
-
什么是傅里叶变换和逆变换?为什么要用傅里叶变换?2024-01-11 6199
-
傅里叶变换的定义 傅里叶变换的意义2023-11-30 3915
-
傅里叶变换和反变换公式2023-09-07 21909
-
傅里叶变换(对信号分析)(下)2023-08-09 1613
-
非周期信号的频谱分析─傅里叶变换PPT下载2018-03-05 945
-
非周期信号的频谱分析─傅里叶变换.zip2017-10-04 1690
-
非周期信号的频谱分析─傅里叶变换2017-10-03 1622
-
非周期信号的傅里叶变换2009-07-27 10265
-
傅里叶变换,建立信号频谱2008-08-05 1603
全部0条评论

快来发表一下你的评论吧 !

