音频失真是什么？了解非线性

了解系统非线性如何在音频信号中产生失真，从而影响我们听到的声音。我们将研究正弦波、谐波和互调失真。

我们花了很多时间思考和谈论音频失真，甚至有时听它，但它到底是什么，为什么它很重要？

失真通常有两种类型：

• 频率失真 — 由带宽不足和带宽限制之间的非平坦频率响应引起
• 非线性失真——由硬件中的非线性引起。

本文是关于非线性失真的，因为如今频率失真在现代设备中很少成为问题。非线性失真通常被错误地称为“非线性失真”。但是，失真不是非线性的，而是硬件设备是非线性的。

正弦波 — 音频信号的构建块

一个好的起点是解释正弦波信号（图1）只有一个频率。在音频频率下，正弦波以单个音调的形式被听到。

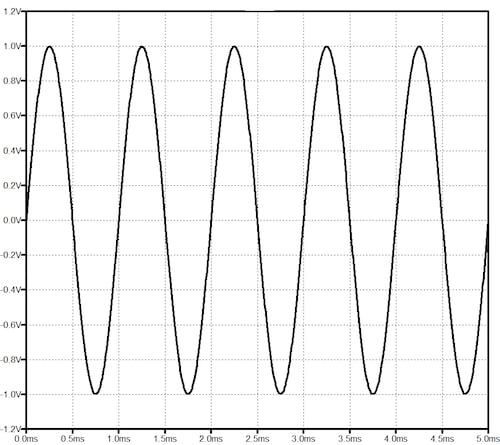
* 图1 .正弦波信号*

设计人员可以从许多正弦波的集合中构建所有其他波形。除了正弦波之外，还可以从其他构建模块信号中建立波形。然而，构建块信号、过程和数学可能要复杂得多。因此，沿着音频路线走下去似乎没有意义。

正弦波由多种形式的自然振动或振荡产生。考虑一个时钟的摆轮，有一个水平轴。如果我们在车轮边缘做一个标记并从侧面看，则轴上方（和下方）标记的高度会在时间上勾勒出正弦波。

非线性导致音频失真

非线性失真是由音频信号路径中的某些设备产生的输出幅度与输入幅度不严格成比例引起的。这可能是音频放大器，甚至是失去光泽的连接器。这种非线性会使信号失真，使得输出波形与输入波形不同。

现在，无论输入波形是什么，它都可以被认为是许多正弦波的总和，输出波形也可以。不过，由于波形不同，输出波形包括输入波形中没有的正弦波分量。它们是扭曲的。

对于输入信号的每个正弦波分量（称为基波），非线性产生该分量频率的倍数的信号，称为谐波。双频谐波称为二次谐波或2阶谐波。三倍频率一是三次谐波。这些新信号是谐波失真分量。

图2显示了来自一个非常糟糕的电路的输入和输出信号，该电路产生20%幅度的二次谐波和10%的三次谐波。在输出中添加二次和三次谐波信号会使信号失真，因此它不再是纯正弦波。选择这些高失真数字是为了清楚地显示效果。

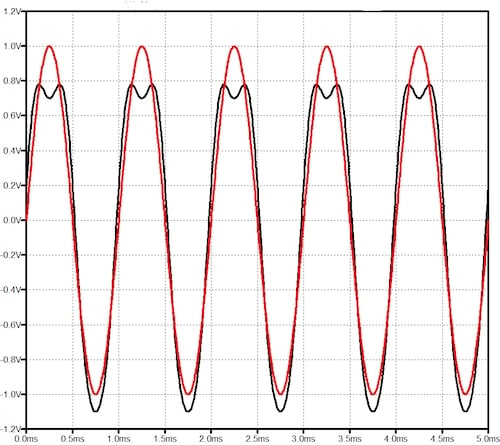
* 图2. 非线性失真示例。纯正弦输入信号为棕色，失真输出信号为黑色。*

二次谐波总是导致正半周期与负半周期的形状不同。在本例中，三次谐波会影响信号的峰值。这是因为我选择了三次谐波相对于基波相位角的相位角来做到这一点。不同的相位角会导致不同的形状变化。

乐器中的谐波示例

几乎所有乐器（和人声）产生的声音都包含许多谐波。例如，正弦波是由ocarina产生的，ocarina是一种类似于口琴的小型手持管乐器，顾名思义，它在每个音符中产生大量谐波。

再添加一些谐波会改变音符的音调或音色。除非添加量很大，否则任何人都很难察觉差异，除非他们能够区分斯特拉迪瓦里的声音和瓜内里的声音。

图3显示了小提琴的“谐波频谱”。频谱通常是功率或电压与频率的关系图。

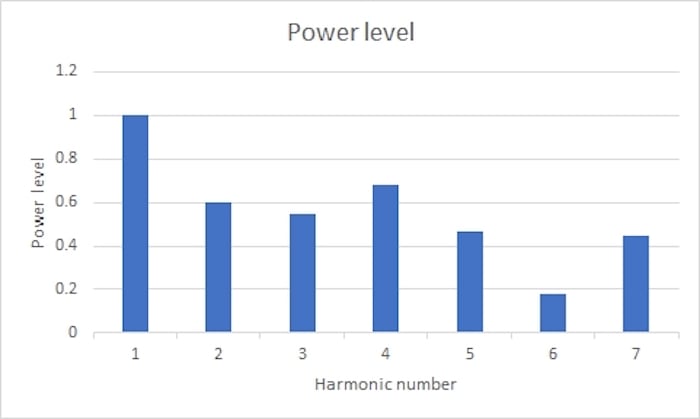
* 图3. 小提琴的频谱显示为谐波倍数*

制作一把好小提琴的艺术是选择木材、它们的处理和它们的形状，以产生最理想的谐波振幅组合。“最需要”可能是“柔和”或“令人兴奋”，具体取决于音乐流派或仅仅是个人喜好。

但是，如果额外谐波的添加很大，则可以听到新的效果。非线性产生谐波恰好是原始频率的两倍、三倍等。大多数仪器产生的谐波实际上应该被称为“部分”，因为它们不是存在的最低频率（基波）的精确倍数。

对于某些乐器来说，这些部分与基本面一样响亮，甚至比基本面更响亮。例如，长笛产生几乎相等的基本和二次谐波。

部分谐波和最接近谐波产生一个新的频率分量，该分量出现在部分和谐波频率之间的差异处。此属性的频率总是比两者低得多，这是一种咆哮，往往会使声音变得粗糙而不是平滑。

还产生了新频率的分量，该分量是部分频率和谐波频率的总和。这个新频率对组合声音的影响不大，但它的频率要高得多，并且可能与更高频率范围内的其他信号分量发生冲突。

值得庆幸的是，除非非线性非常严重，否则新频率分量在差和和频率上的影响很小。

不幸的是，这还不是故事的全部。非线性还导致输入信号中两个分量的每个组合都出现这些和和差频率的信号。这些新频率被称为“互调失真分量”。

互调失真

这些分量要严重得多，即使非线性相当温和，许多新频率的影响通常也非常可听。那么，为什么我们主要讨论和测量谐波而不是互调分量呢？

原因有二。首先，过去测量谐波更容易，但对于现代数字仪器来说，这不是问题。其次，我们用最简单的输入信号——正弦波来测量谐波。

为了测量互调，我们必须至少输入两个信号，它们都可以是正弦波，但是我们应该使用什么频率，它们应该具有相等的幅度（电压）还是不同的？

直到 1970 年代，人们对此有很多困惑，人们做出了不同的选择，因此他们的结果没有可比性。随后，世界大多数音频界的代表在国际电工委员会的一个技术委员会中达成了一项国际协议。该委员会规定了两种互调失真：差频失真（以前称为CCIR失真）和调制失真（SMPTE失真）。

微频失真（见图4）测量由两个相等的高频信号（如1 kHz和19 kHz）产生的20 kHz差频信号的相对幅度。这是一个更重要的评估，因为它是高频线性度的量度，在高频下，负反馈的失真减少效应往往较小。在图4中，19 kHz和20 kHz的输入信号产生两个失真信号：

1. 1 kHz 时的差分信号 （20 - 19 = 1）
2. 39 kHz 时的总和信号 （20 + 19 = 39）

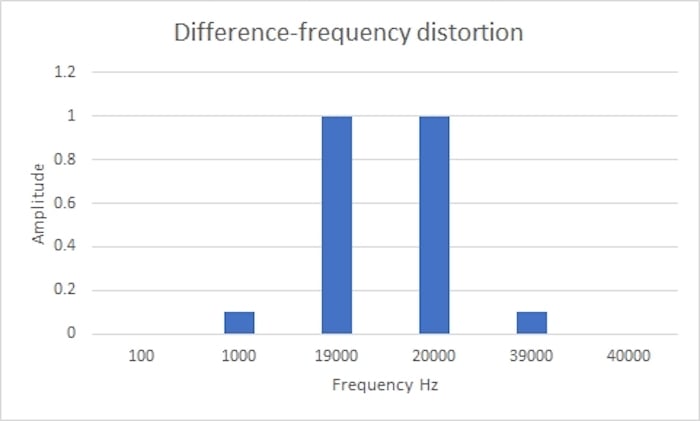
* 图4. 差频失真*

调制失真使用低频信号和较低电压下更高频率的信号，通常是其他信号的四分之一。例如，信号可能是 80 Hz 和 5 kHz。如图5所示，非线性再次产生两个新的输出失真信号分量：

1. 4920 Hz 时的差分信号 （5000 - 80 = 4920）
2. 5080 Hz 时的总和信号 （5000 + 80 = 5080）

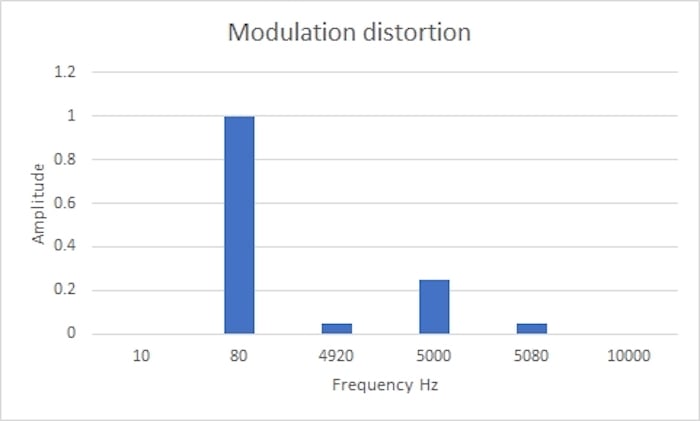
* 图5. 调制失真*

还可以测量由输入信号分量的谐波产生的其他互调分量。例如，如果我们有两个输入频率 f1 和 f2，则在 f2 和 1f2 ± f2 处存在 2f1 ±互调分量，以及我们已经看到的 f1 – f2 和 f1 + f2。但这些并不能告诉我们更多关于被测量设备性能的信息。

我们应该得出的结论是，我们应该消除所有非线性来源，以免损坏再现的声音。然而，我们必须在放大器中使用的设备，即晶体管（或过去的阀门/电子管），本质上是非线性的，因此我们必须使用精心选择的设计技术来尽可能减少非线性。

这经常会引发一个问题，“多少才足够？发烧友经常就人类听觉的敏感性以及我们实际可以听到的失真程度来争论这个问题。但是，对于本文来说，这是一个太大的主题。