罗氏线圈的基本原理

罗氏线圈是做雷电监测系统最常用的雷电流监测传感器，它有许多优点：体积小、重量轻、易安装、无磁芯饱和现象，可测量范围宽、生产成本低，被测电路与测量电路电气隔离等等;

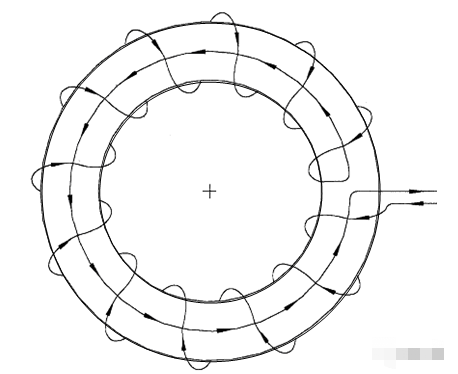
罗氏线圈的基本原理包含两个：法拉第电磁感应定律和安培环路定律。

1、法拉第电磁感应定律

电路中感应电动势的大小，跟穿过这一回路的磁通量的变化率成正比。

公式为：V(t)=ΔΦ/Δt，式中ΔΦ为变化的磁通量;ΔΦ=ΔB*A，式中B为磁感应强度，A为线圈横截面积，那磁感应强度B又应该如何计算呢?这就需要应用安培环路定律。

2、安培环路定律

在真空中，磁感应强度沿任一闭合回路L的线积分，等于该回路所包围的稳恒电流的代数和的m倍。(m为真空中的磁导率)

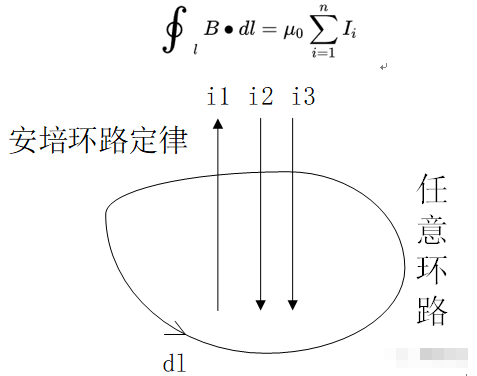
这是严谨的数学表达式，式中说明了电流与磁感应强度B之间的关系，在工程应用上，为了计算简单，先只考虑环路为圆形，且电流从圆心穿过的情况;

2.1无线长均匀载流长直导线的磁场

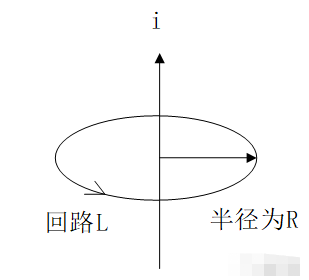
步骤：1)选取半径为R的回路L;

2)计算，q是磁场强度B与dl的夹角;

3)求回路包含电流;

4)用安培环路定理计算磁场;

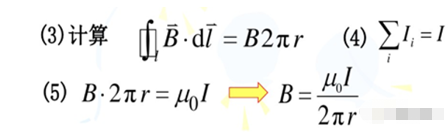
也就是说，在半径为r的环路上每一点的磁感应强度相等且B=mI/(2πr);如果电流i是变化的，那么环路上每一点的磁感应强度的变化量ΔB=mdi/(2πr),相应的磁通量的变化量ΔΦ=ΔB*A=uAdi/(2πr);

2.2无线长圆柱面的磁场

解法：将圆柱面分为无限多窄条，每个窄条可看作电流dI的无线长直导线;

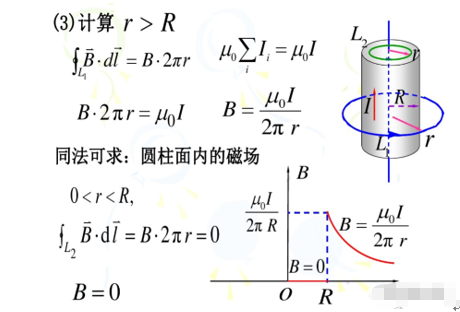
结论：不管电流是从圆柱体中心沿一根直导线流过，还是从空心圆柱面均匀流过，它们在以同心圆R上的圆上的每一个点的磁场强度相同且磁场强度为 B=;

3、罗氏线圈的基本原理

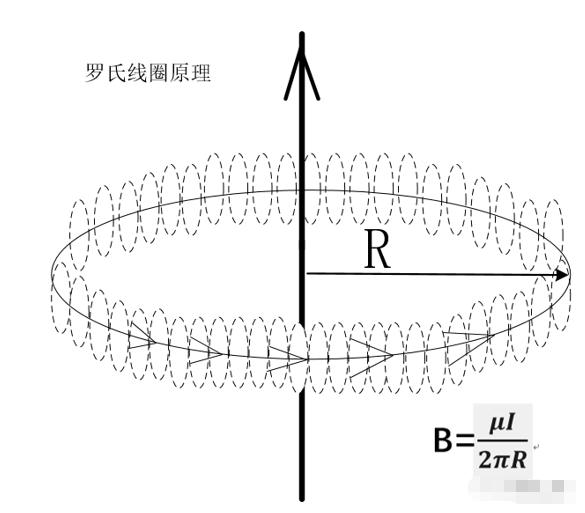
如果电流i是变化的，那么环路上磁感应强度B 也是变化的

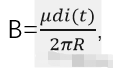
对于单个线圈磁通量也是变化的;

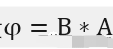
A 是线圈横截面积;

在单个线圈应用法拉第电磁感应定律：

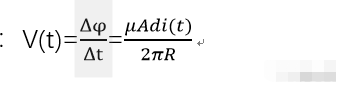
对于N个线圈串联：V(t)=，相当于有N个电压源串联在一起;(假设线圈是均匀绕制的，每个电压源的电压就是相等的)

V(t)=M，其中M=;M通常称为互感系数;

式中：——空气磁导率;

A——线圈横截面积;

N——线圈匝数;

R——传感器的半径;

注意：线圈的感应电动势V(t)和传感器的电感量和内阻是没有关系的。

虽然，我们求出来感应电动势与被测电流是一个微分关系，那么如何把微分信号取出来还原呢?

4、罗氏线圈积分器设计

传感器是由线圈绕制的，在取出信号时，必须考虑它的等效模型，如下图所示;

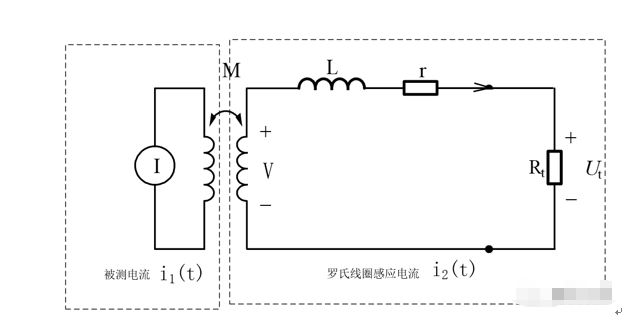
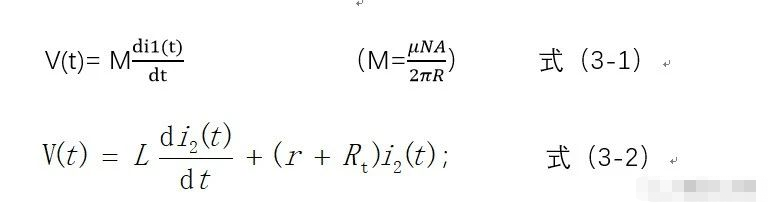
4.1自积分电路

当L足够大， r和Rt足够小，且电流信号频率不能太低(电流变化率大)，则有

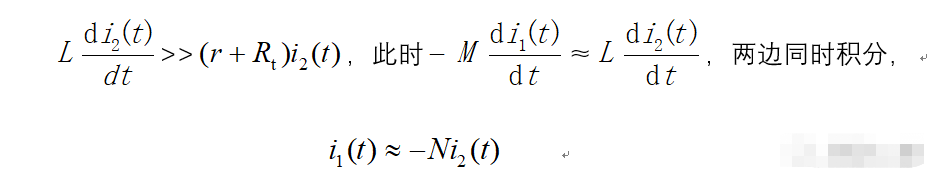
这就是自积分，

自积分工作条件： 电感L足够大(毫亨级)，内阻r，取样电阻Rt足够小(几欧以内)，且电流信号频率不能太低(50HZ以上);

4.2外积分罗氏线圈

4.2.1无源RC积分电路

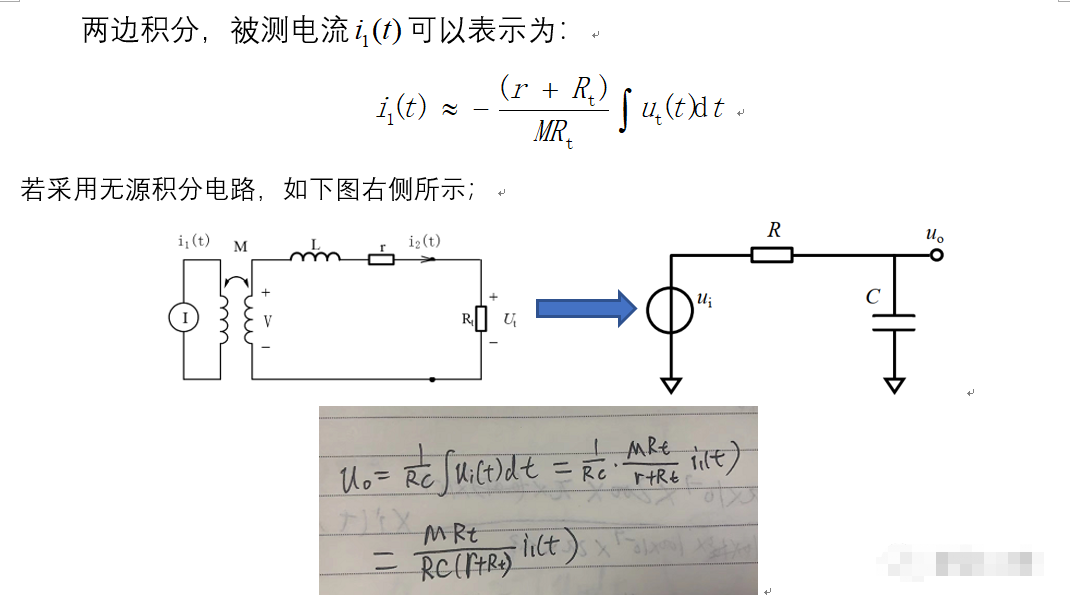
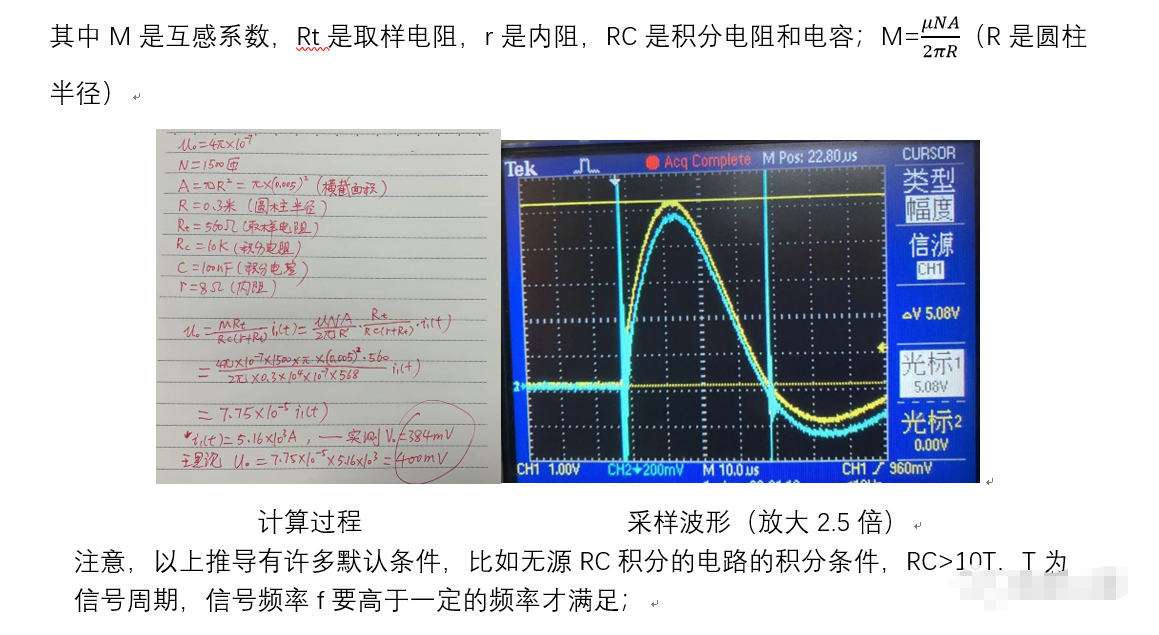
RC无源积分工作条件：电感L足够小(uH级)，取样电阻Rt足够大(100Ω~1K)，信号频率要足够的大，且满足f>10倍的1/(RC)，比如R=10K，C=100nF，则被测信号频率要大于10K;

4.2.2带低频补偿的有源积分电路

无源积分电路其实就是一个低通滤波器，且没有放大功能，当信号频率f>>f0时，则相位Ψ就接近-90度。(f0是特征频率)，当RC太大时，虽然可以还原更低频率的信号，但输出幅值会更小，以至于信号会淹没在噪声中，干扰信号会使信号变形严重;

将无源积分和正向有源积分合并在一起就可以完成一种宽频带积分电路，如下图所求;

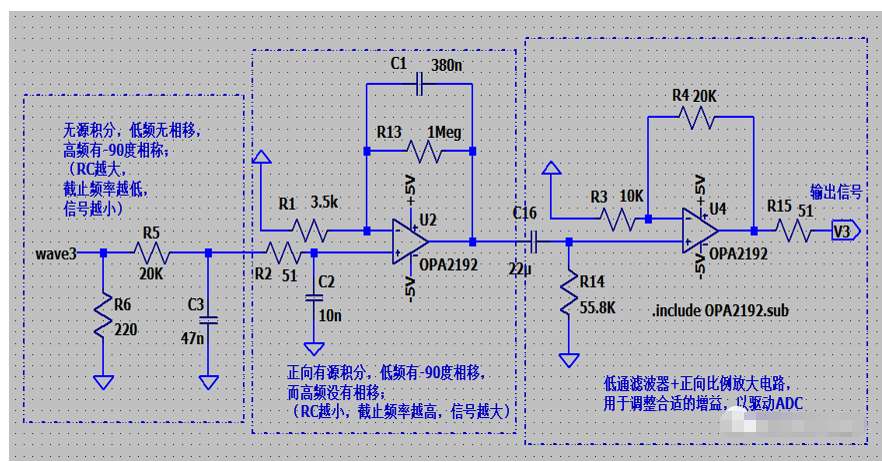
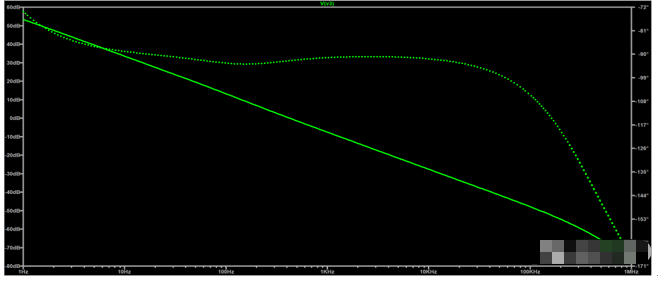
可以看出在低频1HZ~100KHZ都有差不多-90度的相位，增益由低频到高频线性减小，这与传感器低频到高频线性增大正好可以做到一个相对平坦的增益;这样，只要选择合适的无源积分RC和有源积分RC，再加上后面的正向比例放大器，就可以得出一个比较宽的频带范围。