

关于高斯滤波器的响应和逼近
电子说
描述
本文翻译自关于高斯滤波器响应和逼近的文章(1959),作为早期高斯滤波器的实现相关论文,分析和设计方法非常经典,值得精读。
英文原文。
关于高斯滤波器的响应和逼近(On the Response and Approximation of Gaussian Filter)
摘要
本文讨论了一种滤波器,其幅频响应特性为,其中是频率的函数,是与滤波器带宽相关的常数。该滤波器的幅度响应曲线具有高斯概率函数的形状,结果表明,相位响应曲线基本上是线性的。以前的研究人员已经表明,这种滤波器具有出色的瞬态特性,从某种意义上说,它是瞬态信号的最佳滤波器。本文讨论了其对脉冲和阶跃函数的响应。给出了一种设计高斯滤波器的逼近方法,并给出了这种高斯滤波器逼近的实际响应测试结果。
I. 介绍
对于任何输入波形,当网络输出的波形与输入的波形相同时,可以说网络具有理想的瞬态响应。只有纯电阻网络才有这样的响应。一个滤波器,就其应用本质而言必须是具有非恒定频率响应的,所以是不能具有这样理想的响应。滤波器的带宽越窄,其瞬态响应的失真就越大。因此,具有最小幅度响应展宽(amplitude-response spread)和波形失真(distortion)组合的滤波器可称为瞬态“最佳”滤波器。
此处选择脉冲函数和阶跃函数作为代表性输入波形来描述高斯滤波器的特性,因为:1) 这些是瞬态分析相关文献中最常讨论的函数,2) 一旦已知脉冲或阶跃响应,线性滤波器对任何波形的响应都可以通过叠加定理获得。如果带通滤波器相对于其中心频率具有低通模拟和相对较窄的带宽,则可以假设带通滤波器对滤波器中心频率处的波的包络响应与模拟低通滤波器对具有包络形状的波的响应相同。为方便起见,本文主要考虑低通高斯滤波器的响应。然而,结果也适用于上述条件下的带通高斯滤波器。附录Ⅱ描述了一个实用的高斯带通滤波器的设计。
低通高斯滤波器的频率响应特性可以由下式定义:
其中是与带宽相关的常数。这种滤波器的频率响应曲线的形状如图1所示,与高斯概率分布曲线相同。如下所示,高斯滤波器具有出色的瞬态响应特性,并且可以相对容易地进行函数逼近。
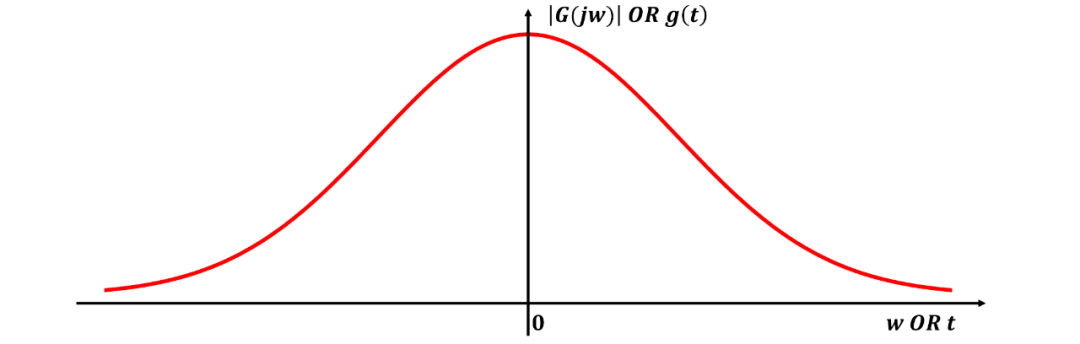
图1 高斯响应曲线
II. 脉冲响应
如果式(1)的低通高斯滤波器的输入信号是单位脉冲,则时域输出由下式给出
其具有图1所示的高斯形状,与滤波器的幅度响应特性曲线相同。通过图2所示的带通滤波器的脉冲响应波形可以看到,该带通滤波器的形状近似为高斯曲线,其具体设计将在第 V 节中进行描述。请注意,是曲线包络具有图1的形状。
让我们来定义:a) 由于滤波器而引起的脉冲失真为时间响应展宽(time-response spread) 的均方值
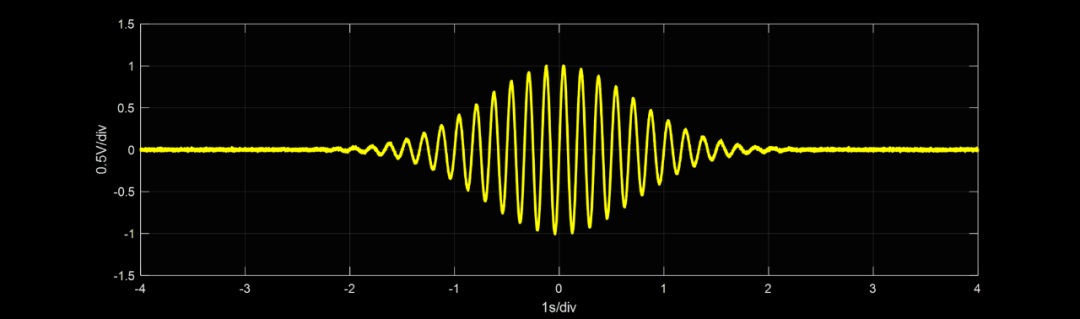
图2 带通滤波器(图8)的脉冲响应示波器显示图
b) 滤波器的幅度响应展宽(amplitude-response spread) 的均方值
最佳的瞬态滤波器应该具有最小的时间和幅度响应展宽的组合。如果最优性标准是
或者是
其中是加权常数。具有式(5)形式的方程已由诺伯特·维纳(N. Wiener, 译注:维纳是控制论创始人, 维纳滤波器发明者)求解得到。和具有式(6)形式的方程由 A. Gabor(译注: 这里应该是D. Gabor即Dennis Gabor,就是大名鼎鼎的因全息技术而获得诺贝尔获的丹尼斯·加博尔)求解得到。
现实工程实践中出现的许多脉冲在形状上都非常接近高斯曲线。通过高斯滤波器后的高斯脉冲将保持其高斯形状,但会在时间上展宽(spread out)。这可以表示如下:
让高斯输入脉冲由下式给出
其中是决定脉冲展宽的常数。然后
从式(1)和式(8)可以得出
然后
很明显,任何数量的高斯滤波器级联都将具有高斯的组合传递函数(combined transfer function)。
III. 阶跃响应
阶跃函数是脉冲函数的积分。鉴于系统假定是线性的,高斯滤波器对单位阶跃的响应是此类滤波器对如式(2)所给出的单位脉冲响应的积分,
该等式的曲线绘制在图3中。我们所构造的高斯带通滤波器对中心频率调制的阶跃函数的响应波形如图4所示。请注意,曲线包络具有图4的形状。图3的响应特性显示无过冲(no overshoot)、无振铃(no ringing)、无拖尾(no smear),并且波形关于其半值点完全对称。对称性是高斯滤波器线性相位响应的结果。此外,这意味着过渡是最陡峭的。低通高斯滤波器的(带宽上升时间)乘积为 0.343,如果响应有非常小或没有过冲,这非常接近可能的最低值。此(带宽上升时间)乘积的计算在附录 I 中给出。简单的 RC 低通网络的 (带宽上升时间) 乘积为0.35非常接近高斯滤波器的。然而,高斯滤波器的幅频响应曲线的截止频率的滚降要高得多。事实上,需要使用无限多个级联的 RC 网络才能获得高斯响应曲线。
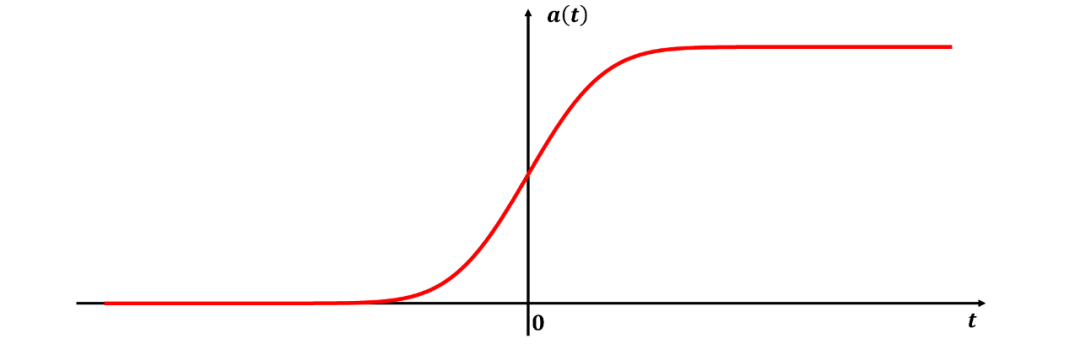
图3 高斯滤波器阶跃响应
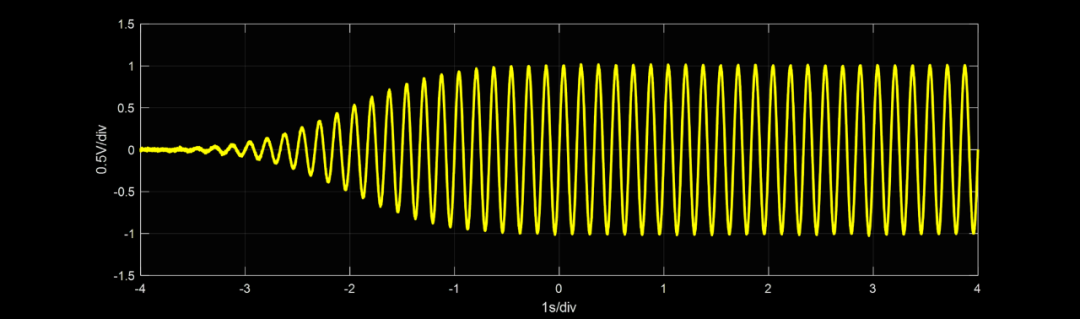
图4 带通滤波器(图8)的阶跃响应示波图
在通带中具有零衰减和在阻带中具有无限衰减的矩形滤波器有时被称为“理想”滤波器(ideal filter)。这种低通滤波器的阶跃响应是如图5所示的函数。
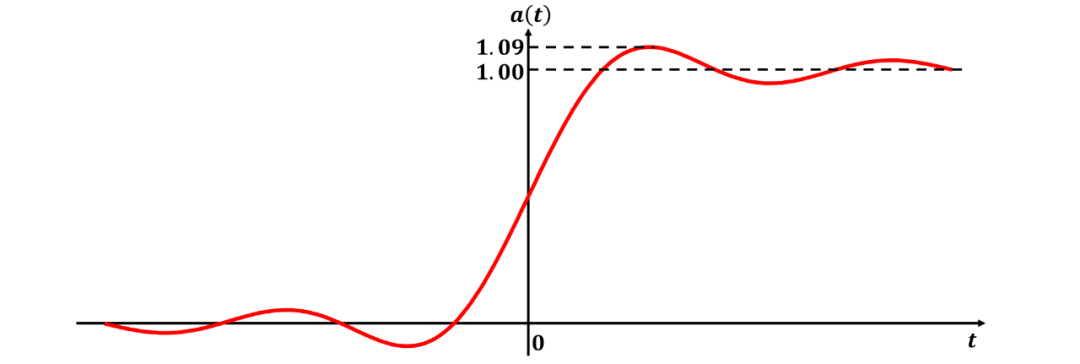
图5 矩形滤波器的阶跃响应
它有 9% 的过冲和 0.445 的 (带宽上升时间) 乘积。因此,虽然这样的滤波器具有比高斯滤波器更陡峭的截止频响,但它不是瞬态的理想滤波器。此外,矩形响应特性比高斯响应特性更难逼近。通过巴特沃斯、切比雪夫或勒让德多项式对矩形响应特性的逼近导致滤波器具有比相同阶数的高斯滤波器更锐的截止频率滚降,但此类滤波器不可避免地会产生明显的过冲,这主要是由于其相位响应特性的非线性所导致的。
与滤波器的瞬态响应密切相关的一个问题是滤波器对变频率信号的响应。对于频率随时间线性变化的信号,在其性能明显改变之前,高斯滤波器的扫描速度大约是矩形滤波器扫描速度的八倍。高斯滤波器不会显著的改变其性能的条件是,其中是以为单位的扫描速率,是以为单位的滤波器带宽。(译注:在频谱分析仪中,其中的中频滤波器就是高斯响应滤波器,其中RBW就是在调整滤波器的带宽)
IV. 相位响应
我们必须在这里区分“理论”高斯滤波器和通过物理器件获得的“可实现”的高斯滤波器。理论上的低通高斯滤波器是其频响由式(1)给出的滤波器,将其重写为
即,理论上的低通高斯滤波器对所有频率都具有零相移。由于我们通常不能同时规定物理上可实现的传递函数的相位和幅度,我们最多可以让
并检查相位函数是否存在使得
能在物理上实现。
可以证明,式(13)的幅度响应函数不可能附加相位函数,因为式(13)不满足佩利-维纳准则(Paley-Wiener criterion):
图1和图3也显示了为什么不存在这样的相函数。注意到,高斯滤波器对在处所施加的脉冲或阶跃函数的时间响应从开始。显然,物理网络不是预测器,即在施加激励之前它可能没有任何响应。因此,如果响应要从而不是开始,则有必要将响应延迟无限长的时间。同样的问题出现在任何锐截止滤波器中,包括图5的矩形滤波器。然而,下面将显示高斯滤波器的相位响应可以假定为线性的。
一种低通高斯滤波器的逼近方法是使用大量具有级联放大器的低通 RC 网络。这样一系列相同级的相位函数 (滤波器的-截止点为其) 是
其中是表示级数的整数。对于
式(16)变为
即相位响应是线性的,斜率为。当时,幅度响应接近高斯函数式(13),相位响应接近完美线性和无限的斜率值。
当使用伯德图时,会得到类似的结果。任何频率的相角由给出,即
其中是以奈培(neper)为单位相对应于的衰减。
其中
因此有:
这是无法实现的。通过集总物理元件构建的任何滤波器的频率响应可以表示为以为变量多项式的比率。
在极高频率下,只有具有最大指数的项才有效,即,对于极高频率,幅度响应由下式给出
其中是高频极限下有效元件的数量。
通过集总物理元件实现的高斯滤波器的幅度响应,无论怎么逼近,都将在高频极限由式(21)而不是式(19)给出。现在假设一个可实现的低通高斯滤波器的幅度响应由式(19)给出,直到频率,该频率远高于任何感兴趣的频率,并且对于所有超过的频率,由式(21)给出。忽略过渡区域,则式(18)可以写成
因此,随着滤波器逼近于高斯滤波器的区域增加,相位响应线性区域及其斜率也增加。
线性相位响应是我们所希望的,因为对于给定的幅度响应特性,它会产生最小的瞬态失真,因为线性相位响应意味着每个频率分量的时间延迟都相等。一般而言,期望相位响应线性度最好延伸超过幅度响应曲线下面积的 90% 以上,这对于高斯曲线来说大约是12dB的范围。
图6显示了测试的滤波器的相位响应,其中也显示了幅度响应。可以看出,线性相位延伸到了重要的低衰减区域以外。该滤波器的脉冲响应和阶跃响应的波形如图2和4所示。这些响应的对称性证实了相位响应线性度延伸到频率响应特性的相当大的部分。
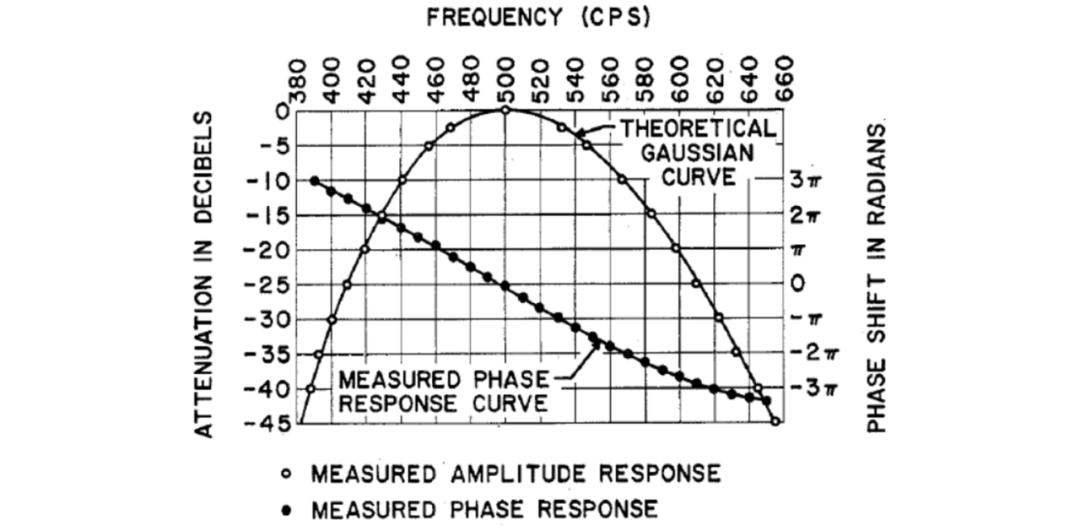
图6 滤波器(图8)的幅频和相频响应
V. 逼近和实现
如第 IV 节所描述的,高斯滤波器可能仅以无限延迟为代价才能实现,因此需要无限数量的元件。这也是其他锐截止滤波器的情况,例如矩形滤波器。然而,高斯滤波器在最重要的区域 (即低衰减频带) 上相对容易逼近。许多研究者建议使用一系列 RC 低通网络和放大器级联以逼近高斯形状,但这并不代表放大器级的最有效的利用。
如果使用更有效的级间耦合网络,则可以用更少的级来逼近高斯滤波器。Wente提出了一种方便的方案,如图7所示的串联峰化(series-peaking)类型滤波器。除其他优点外,它具有简单的低通模拟电路结构。
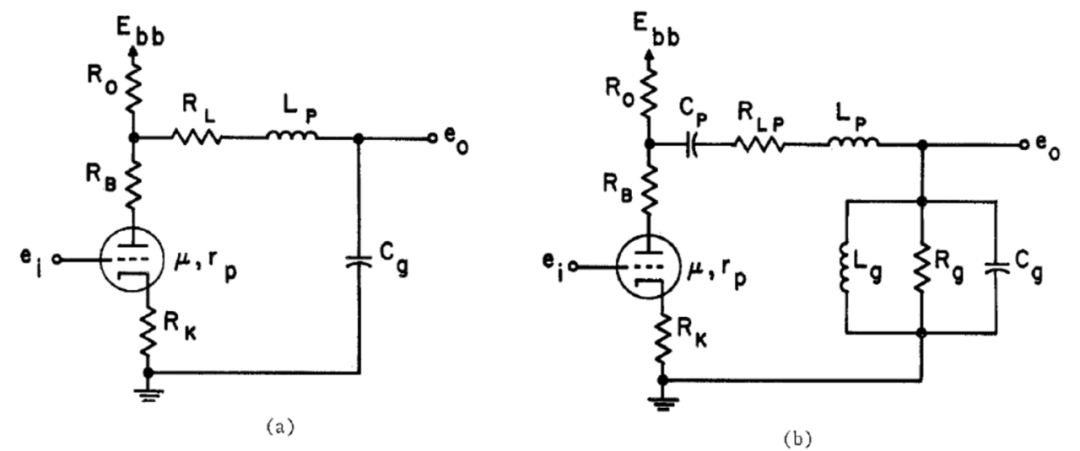
图7 Wente提出的串联峰化网络。(a) 低通 (b) 带通
假设需要通过5级级联进行逼近,然后网络元件值最好通过高斯函数的幂级数展开来获得,如下所示:
1) 设要实现的高斯滤波器的幅度响应为
其中对于低通滤波器:,对于带通滤波器:
是与带宽相关的常数。
2) 对高斯函数的平方幂级数展开直到 20 次方:
是可实现函数。它的分母是,它的所有极点都在左半平面。
3) 利用以下关系找到:
代入,并仅使用平面左半部分的因子,得出
和的值可以从式(24)和式(25)中获得。高斯函数逼近于的具体实现,如式(26)中给出的,即,乘积通过图7所示类型电路的5个级联得到5个左半平面多项式。
4) 通过比较式(26)的每个多项式因子与图7网络的传输方程,从而获得每个级间网络的元件值。
从式(25)可以得到,第1-3级具有单调下降的幅频响应,而第4和5级具有双峰幅频响应。附录II给出了5级带通逼近高斯滤波器的设计方程。(该滤波器的原理图如图8所示,其测得的频率和相位响应如图6所示)。上述幂级数逼近如图9的曲线(d)所示。曲线(a)是理论的高斯曲线。曲线(b)是归因于汤姆逊(Thomson),他的逼近基于最大平坦时间延迟响应。曲线(c)归因于Wente,他使用了图7(a)中所示的5个电路级联,每个级的值为。幂级数展开给出了对高斯形状的最佳逼近,如图9所示。
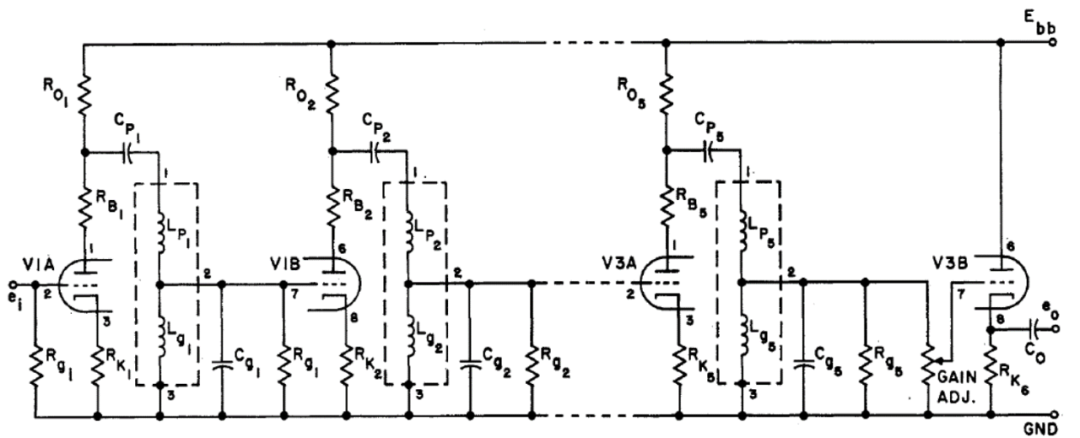
图8 高斯带通滤波器的5级逼近电路图
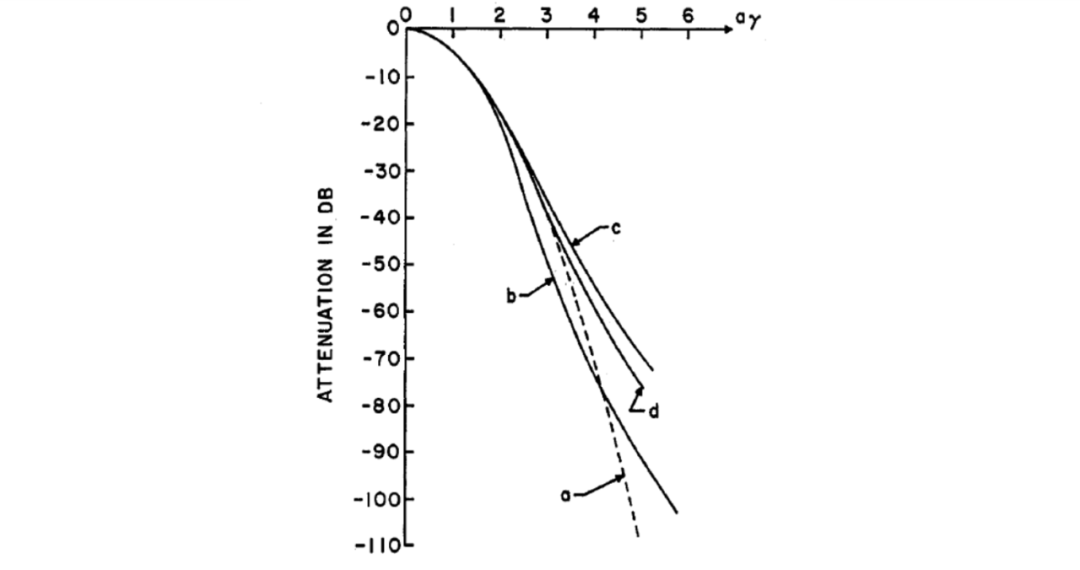
图9 高斯响应逼近: (a) 理想高斯滤波器曲线 (b) 汤姆逊逼近 (c) Wente逼近 (d) 幂级数逼近
VI. 结论
已经表明,高斯滤波器具有优异的瞬态特性,这可以从其脉冲和阶跃响应以及其对可变频率信号的响应中得到证明。它还具有线性相位响应、相当尖锐的幅频截止响应,并且相对容易逼近,这一点可以从5个级间耦合网络的逼近值降到约45dB的事实中得到证明。
附录 I
高斯滤波器的 (带宽上升时间) 乘积
低通高斯滤波器频率响应由下式给出
根据3dB带宽求解,可以得到:
对于低通高斯滤波器,单位阶跃响应由式(11)给出
此函数以如下形式列出
如果我们令,我们得到与式(28)相同形式的式(11),即
以表示的 (0.1 到 0.9) 上升时间为 2.6,并且
然后 (带宽上升时间) 乘积
附录 II
带通滤波器逼近的设计公式
逼近值由式(26)给出
是根据的获得的,如下所示:从式(23)
其中是带通滤波器的中心频率,是3dB带宽。
式(26)现在可以写成以下形式
和的值作为(电路级编号) 的函数是从式(24)、(25)和(32)中获得的,如下表所示:
| Stage Number | ||
|---|---|---|
| 1 | 0.1904 | 1.1527 |
| 2 | 0.1817 | 1.2395 |
| 3 | 0.1647 | 1.4497 |
| 4 | 0.1395 | 1.9059 |
| 5 | 0.1057 | 3.1221 |
图7(b)电路网络的等效电路如图10所示
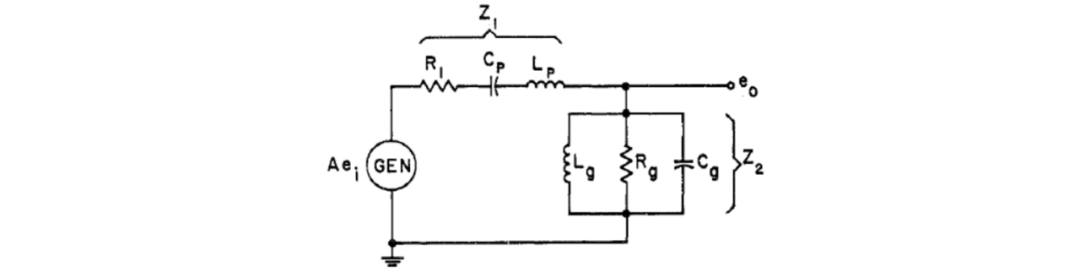
图10 图7(b)电路网络的等效电路图
经过以下变换后:
图10网络的传递函数由下式给出
其中和和与通常定义的一样,分别指的是和(图10) 。
现令式(33)和式(36)的系数相等,即
如果图7所示管子的参数是电子管在阳极电流时的参数,则每级在的增益取为,并且同时联立以上方程,需要的设计方程为:
其中
其中是在的值。
和已给出。我们现在有 9 个未知数:和和以便包含和的调谐电路在处谐振。在剩下的 7 个未知数中,3 个可以由设计者选择,另外 4 个从式(38)到式(42)获得。
建议选择和而不是其他变量。和是最昂贵的元件,而是对每级增益至关重要的元件。例如,在整个滤波器 (或整个滤波器组,如在频谱分析仪中) 中选择相同的和是可能的,也是可取的。通常,每个级所需的和会有所不同,但这些可以很容易地通过额外串联或并联的电阻来进行调整。
审核编辑:汤梓红
-
二阶压控电压源低通滤波器设计2010-05-28 4889
-
求助 高斯脉冲成形滤波器2013-04-11 4623
-
一文了解高斯滤波器,附原理及实现过程2019-09-04 3926
-
具有快速响应的有源滤波器2009-04-15 642
-
高斯滤波器在实时系统中的快速实现2009-12-08 1217
-
高斯滤波简介,高斯滤波性质及应用2018-04-09 26425
-
高斯滤波器的原理和实现2019-09-01 9179
-
Matlab低通滤波器设定与实践2021-08-16 16339
-
高斯滤波器的工作原理及实现方法2022-04-27 8150
-
有源滤波器中的相位响应2023-01-06 3654
-
和ChatGPT聊聊高斯滤波器设计2023-03-29 1263
-
高斯响应滤波器设计2023-05-11 3055
-
模拟无源滤波器设计(九)-Gaussian滤波器设计详解2023-05-28 10004
-
滤波器的群延迟是什么?2023-12-18 7046
-
数字滤波器的频率响应与模拟滤波器的频率响应有何区别2024-02-05 2692
全部0条评论

快来发表一下你的评论吧 !

