使用互调多项式和有效位数对ADC进行建模

在本文中，我们将讨论如何在系统仿真中对ADC进行建模的另一种方法，这次是使用有效位数，并通过在理想量化器输入中引入5阶多项式来调整ADC。

到目前为止，在本系列中，我们已经讨论了各种优点 在系统仿真中对数据转换器进行建模的方法，特别是通过使用 使用有效位数或ENOB的建模方法.

现在，我们将通过添加一个新元素来继续讨论：直接调整我们的ADC模型，在理想量化器输入中添加一个5阶多项式。 

我们的新ADC模型的描述

我们上一篇文章中介绍的模型没有产生任何明显的杂散频率（杂散）。由于杂散是ADC性能的一个重要特性，因此需要更好的模型。

如图 1 所示。

 

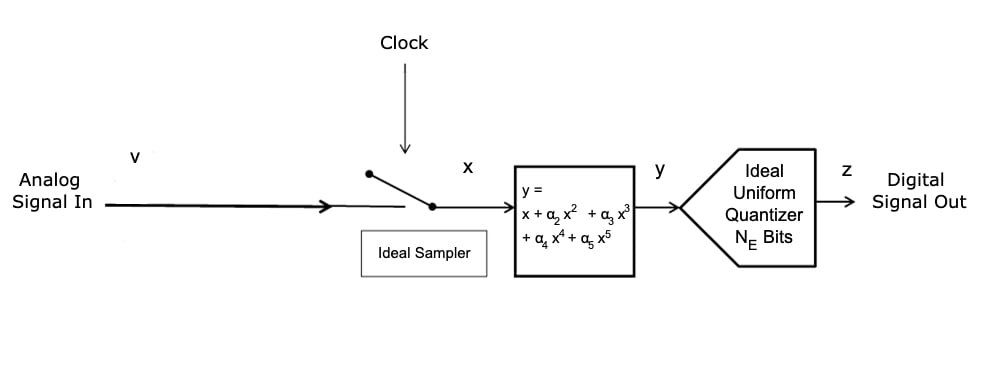
图1.

这将向理想的量化器输入添加一个 5 阶多项式。

应使用双音输入来确定参数α我（fc） 和 NE（fc);其中 fc 是音调之间的中心频率，如图 2 所示（您将从 我们的第一篇文章).

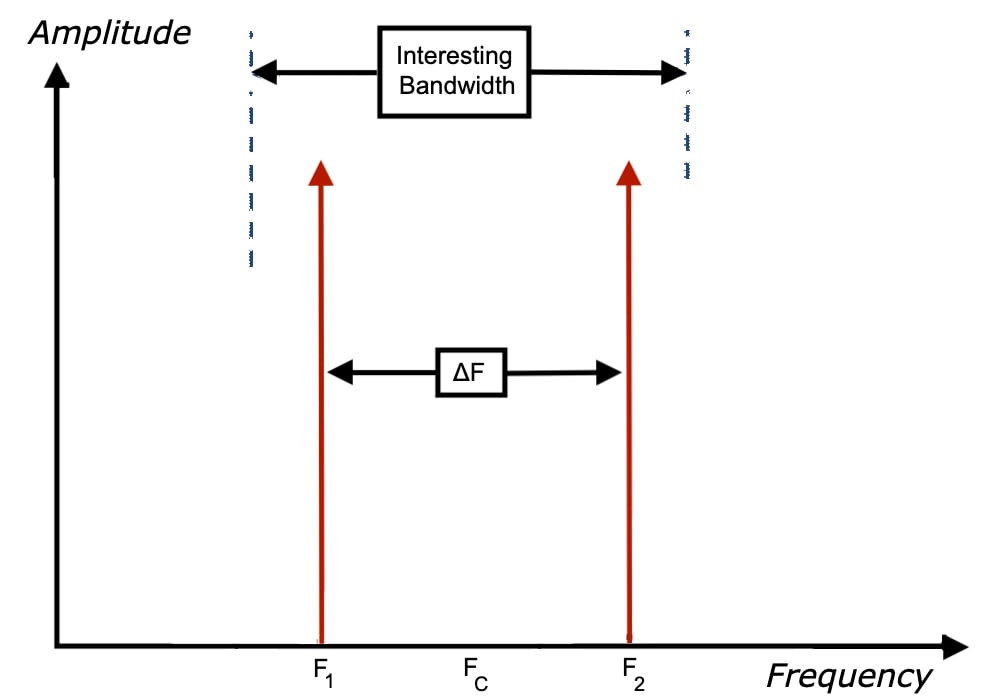
图2.

如果这些参数中的任何一个也是Δf（音调之间的间隔）的函数，则ADC中的存储器可能存在非线性，并且该模型将不适用。 

例如，图3所示的双音输入（从图3中讨论 我们上一篇文章） 使用，其中 NE = 8 位，α3 = 0.04，以及所有其他α我 = 0。存在与我们上一篇文章相同的奈奎斯特带宽（730.9 MHz）和“有趣带宽”（233.7 MHz）。

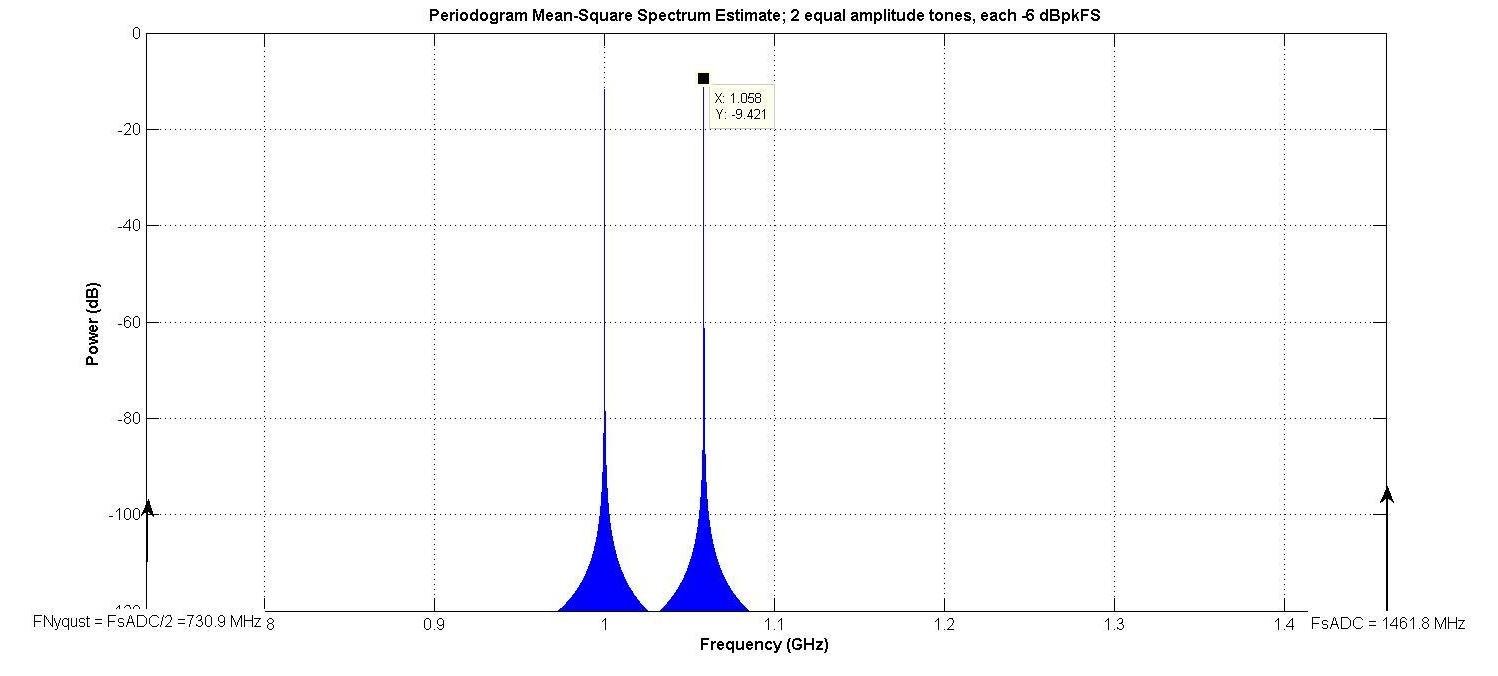
图3.

图4显示了单音输入的输出，图5显示了双音输入的输出。

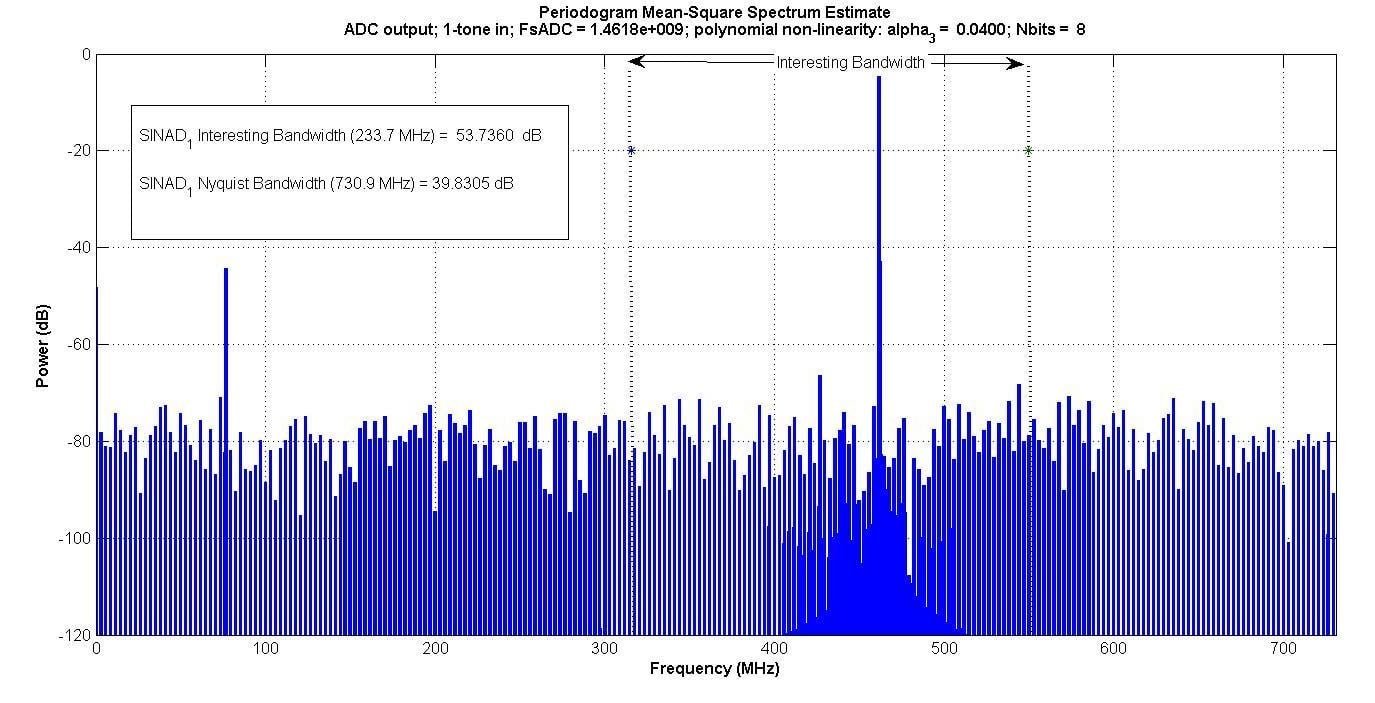
图4.

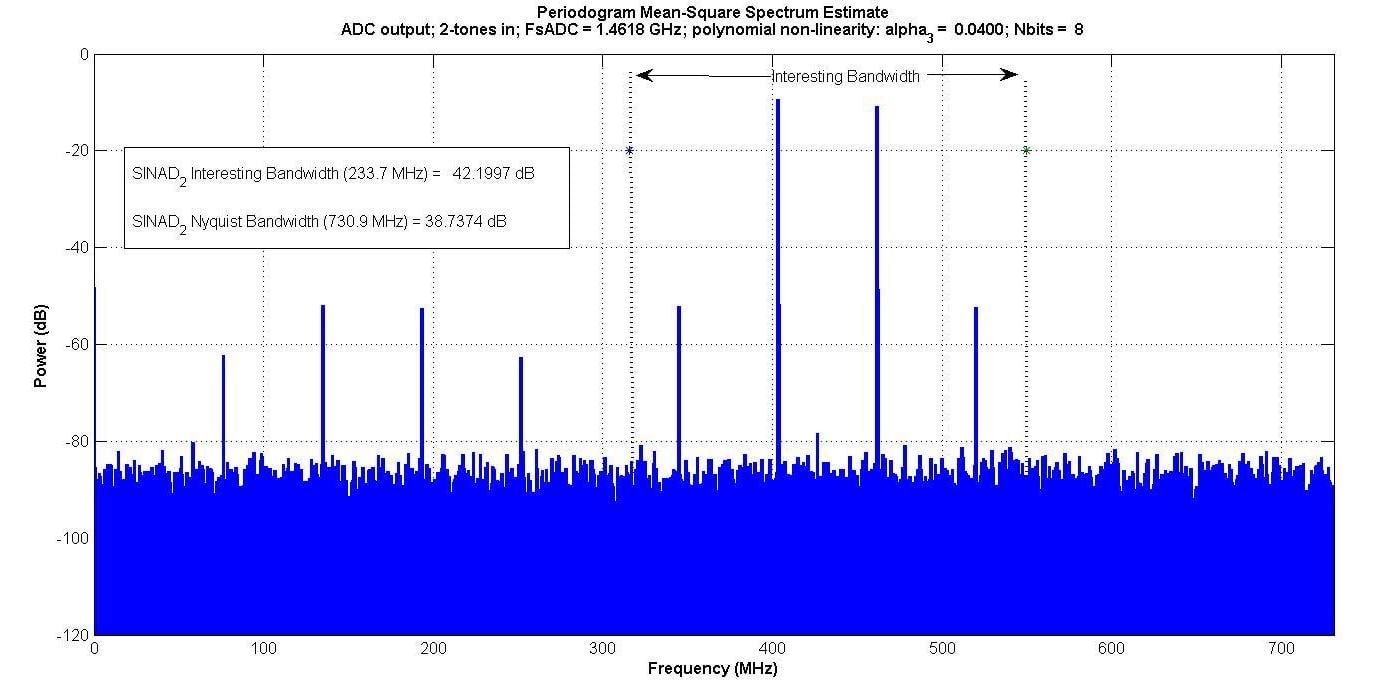
图5.

互调产物出现在双音输入的“相关带宽”内，但单音输入则不然。

如果有人只在这个“感兴趣的带宽”内进行测量——例如，如果有一个数字带通滤波器只通过该频段——单音测试不会捕获互调效应，但双音会。

图6绘制了5至12个输入位的各种SINAD。很明显，以“相关带宽”测量的单音输入不会捕获超过7位的互调效果。

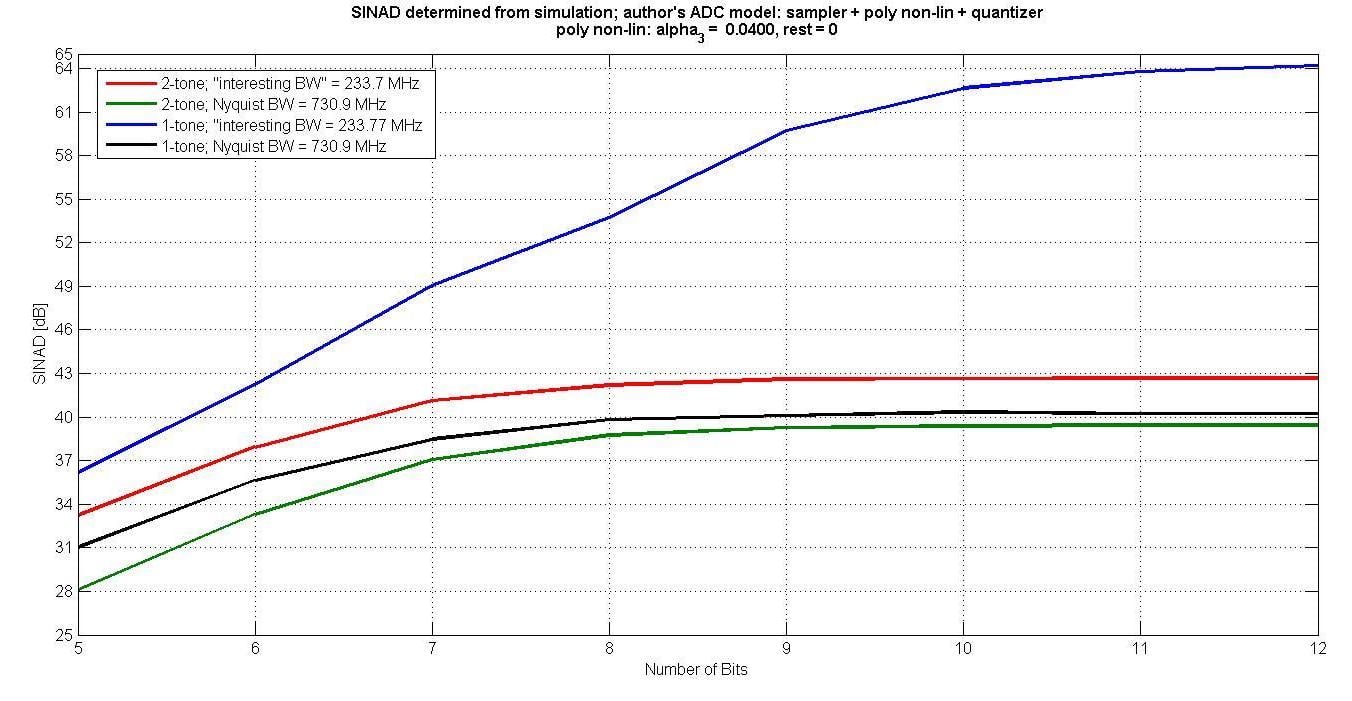
图6.

此外，对于超过7位，由于量化噪声随着位数的增加而降低，但互调失真保持不变，因此SINAD不会随着位数的增加而改善。

与制造商模型的比较

亲爱的读者：你现在可能想知道;“那又如何？这些只是一些模型及其对某些信号的响应。目的是什么？

目的应该是可以在ADC上进行双音测量，并选择图1所示的参数值，以使其最适合测量的ADC输出。这通常可以手动调整它们，直到获得良好的配合。然后，简化的模型可用于长误码率（BER）仿真。

测量可以在实际设备上完成，也可以在设备的良好模型上进行，也可以从制造商的数据表中获得。

要成为一个好的模型，它必须与实际设备非常接近;比如一个完整的SPICE模型。如此复杂的模型在 BER 仿真中运行需要很长时间。

您的作者可以从制造商那里获得他们所谓的“行为”模型，他们声称该模型捕获了特定模型ADC的所有重要参数。制造商的型号还考虑了内部和外部时钟抖动。这用于评估该方法。

双音输入

图 7 显示了仿真设置。生成双音输入，然后输入到作者和制造商的模型中。两者都通过光谱分析显示。 

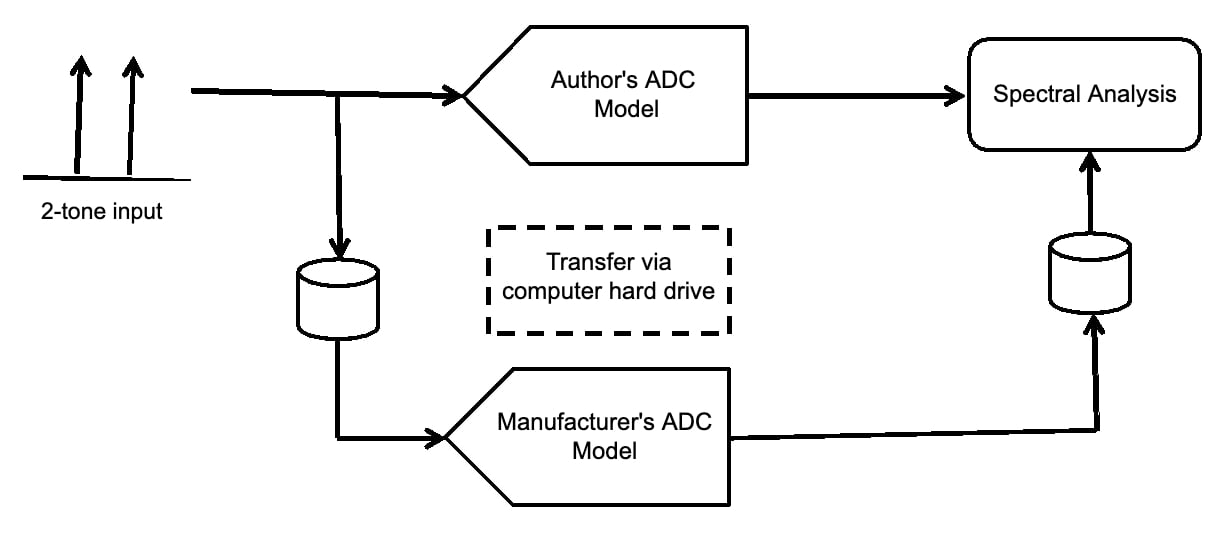
图7.

图 8 显示了使用的输入。两种音调在 300 到 350 MHz 之间。ADC采样频率约为250 MHz，因此这些音调位于第三奈奎斯特区。

由于每个峰值FS为-6.02 dB，因此当它们加入相位时，电压将是两倍，从而产生0 dB峰值FS。

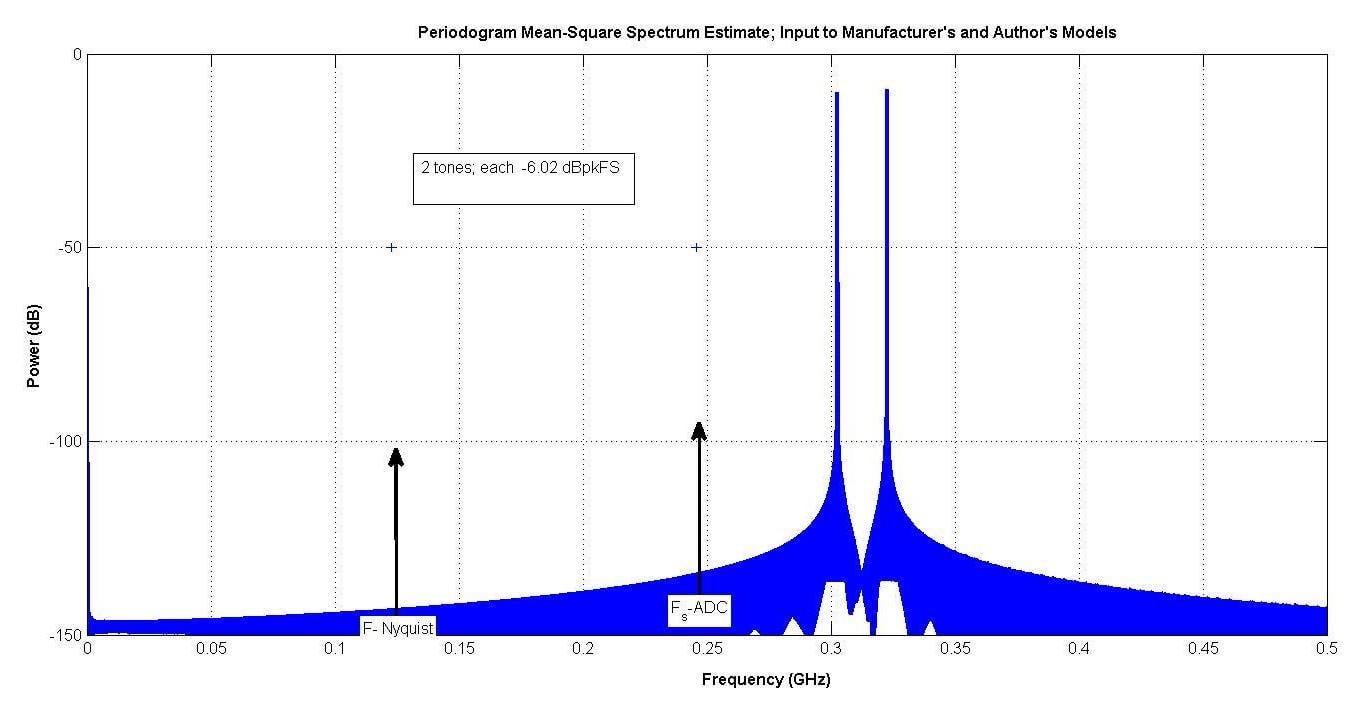
图8.

图9显示了制造商型号的输出，在大约27至107 MHz的“相关带宽”中，SINAD为63.74 dB。

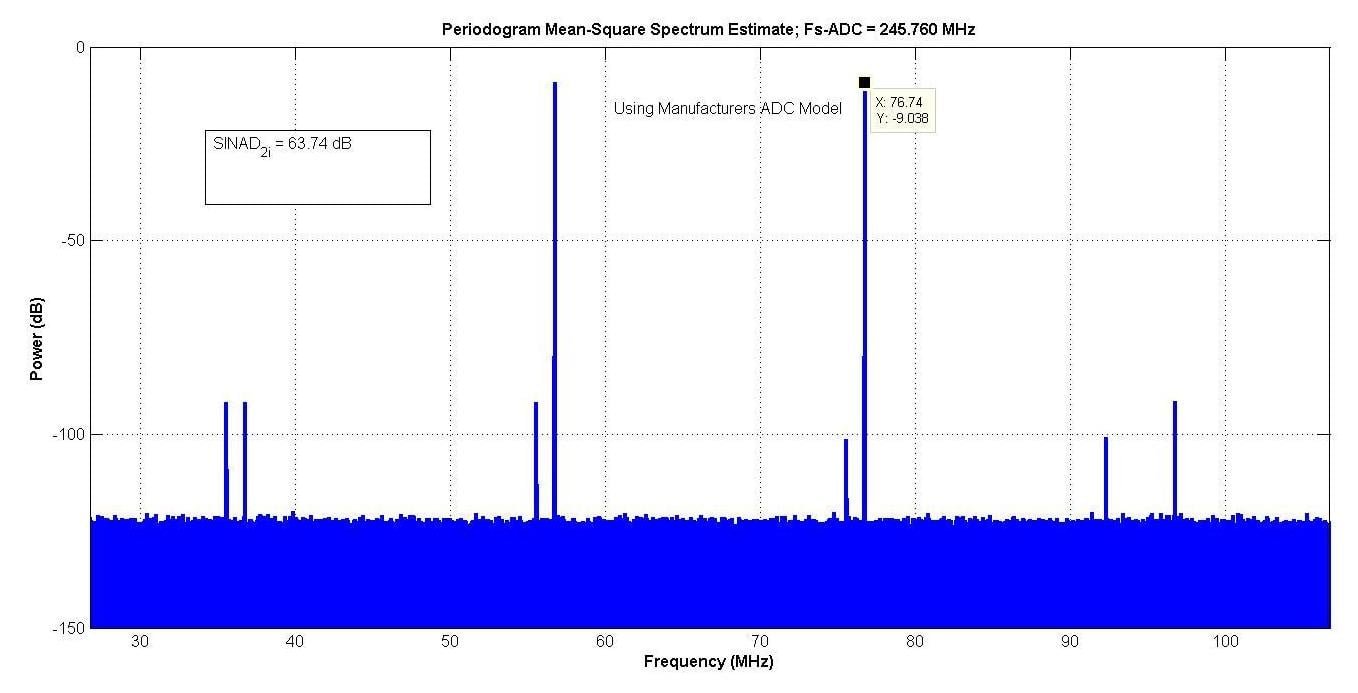
图9.

图 10 显示了调整作者的模型参数以进行匹配后的结果。

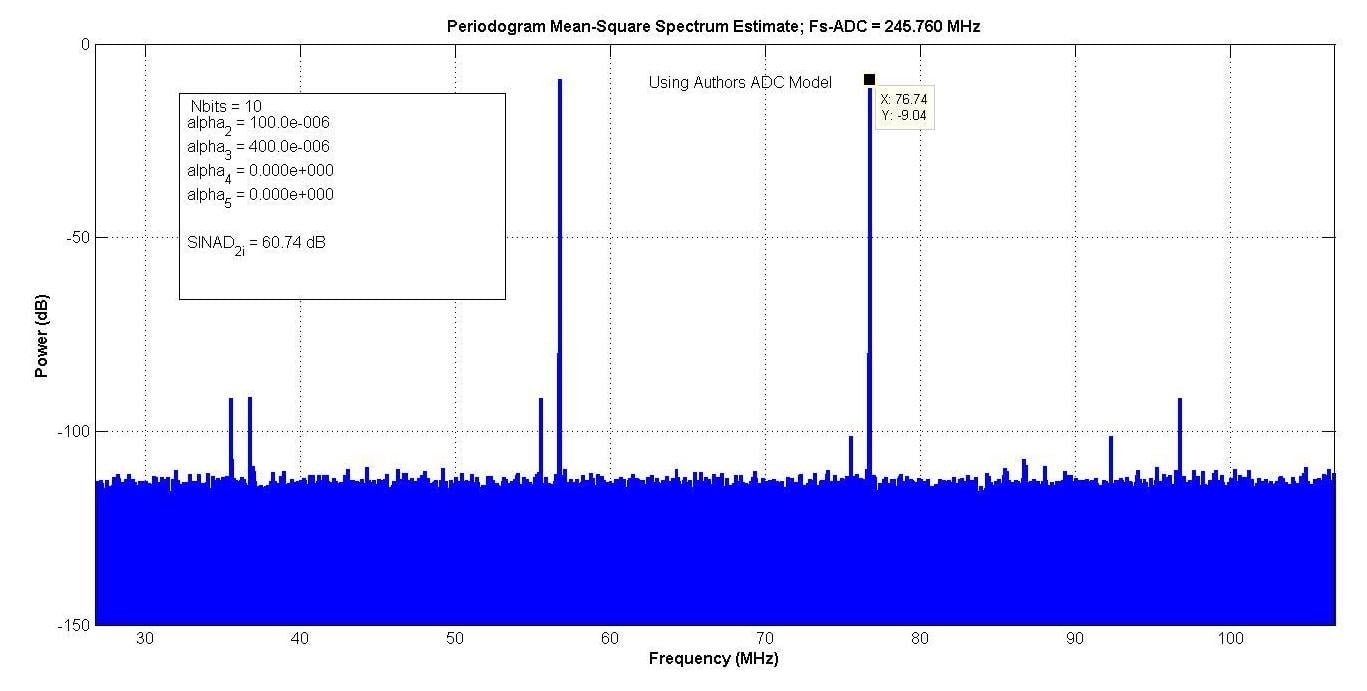
图 10.

多项式系数提供了足够的自由度，因此可以与杂散进行几乎完全相同的匹配。NE 的 11 位，本底噪声比制造商型号低 3 dB，NE 的 10 位使其比制造商的型号高 3 dB。

您的作者决定使用 10 位的悲观值，这给出了 60.74 dB 的 SINAD。改进的模型将允许添加高达6 dB的加性白高斯噪声，因此N的值越高E 可以选择，并添加额外的噪声以匹配本底噪声。

OFDM 波形输入

现在可以将这两个模型与通信波形作为输入进行比较。

商用软件包附带 LTE 型号;生成 OFDM 信号。该模型包括一个调制器、一个频率选择性瑞利衰落通道、加性白高斯噪声和解调器。

可以将ADC模型插入解调器前面，并评估ADC输出的频谱和OFDM信号的误差矢量幅度，如图11所示。

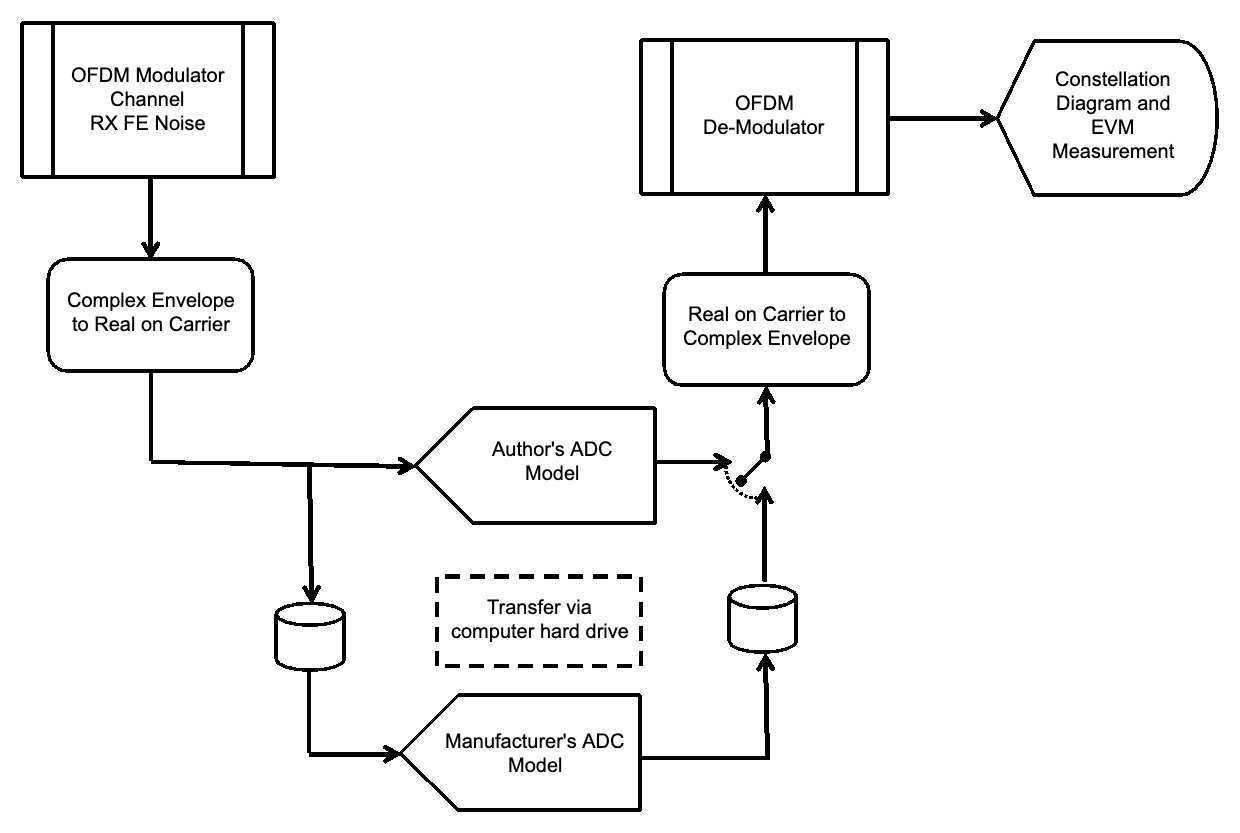
图 11.

使用具有 64-QAM 副载波的 OFDM 信号。您作者的 ADC 模型的参数与图 10 中使用的相同。

商用软件包使用复杂的包络符号 [3] 来形成其信号。这仅允许调制信息通过复数逐个样本地进行跟踪，并且载波频率仅保持为已知常数。因此，描述波形所需的样本数量大大减少。

但是，ADC 模型的输入需要是显式载波上的真实信号，以考虑作为输入频率函数的 ADC 性能差异。因此，需要完成“载波上的复包络到实数”和“载波上的实数到复数包络”的转换 [3]。

图12显示了两个ADC模型的OFDM信号输入。它以与图8所示的双音相同的频率为中心。

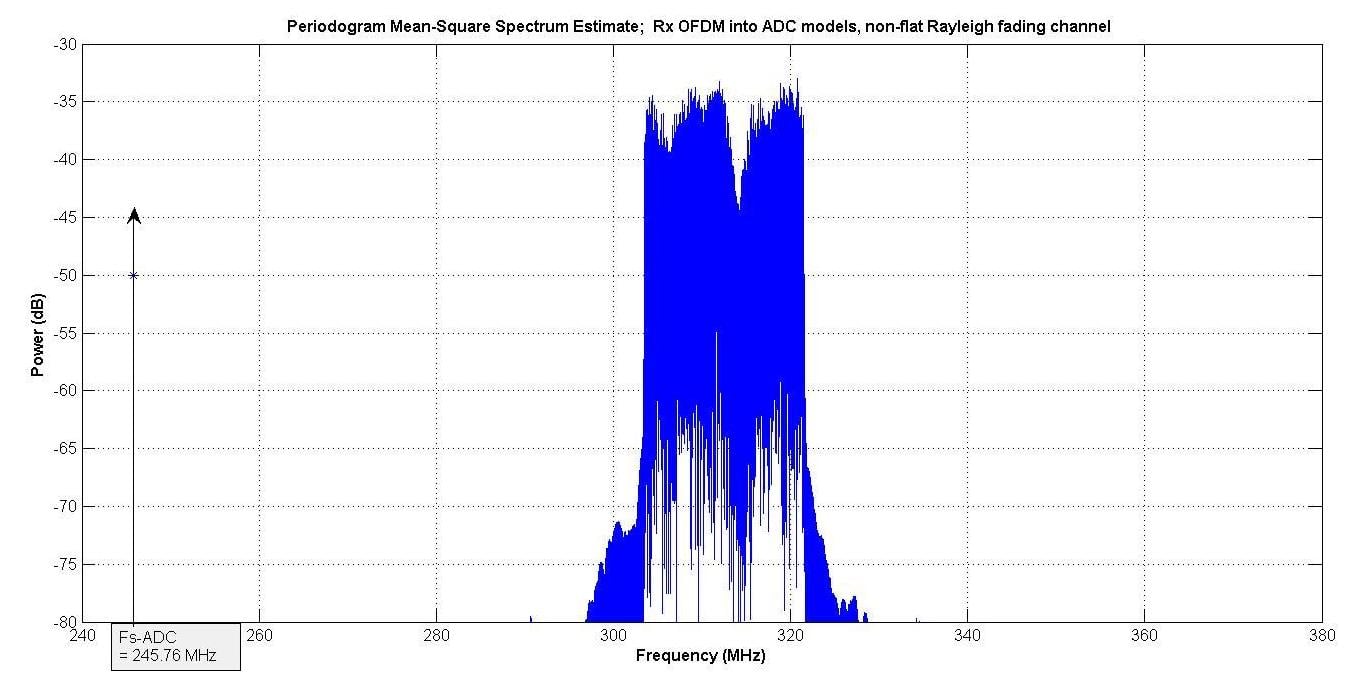
图 12.

两种ADC模型中的dBrmsFS水平均为-7 dBrmsFS。

图 13 显示了制造商模型的频谱，图 14 显示了作者模型的频谱。由于ADC的非线性，两者都显示出频谱再生。光谱非常接近。 

 

 

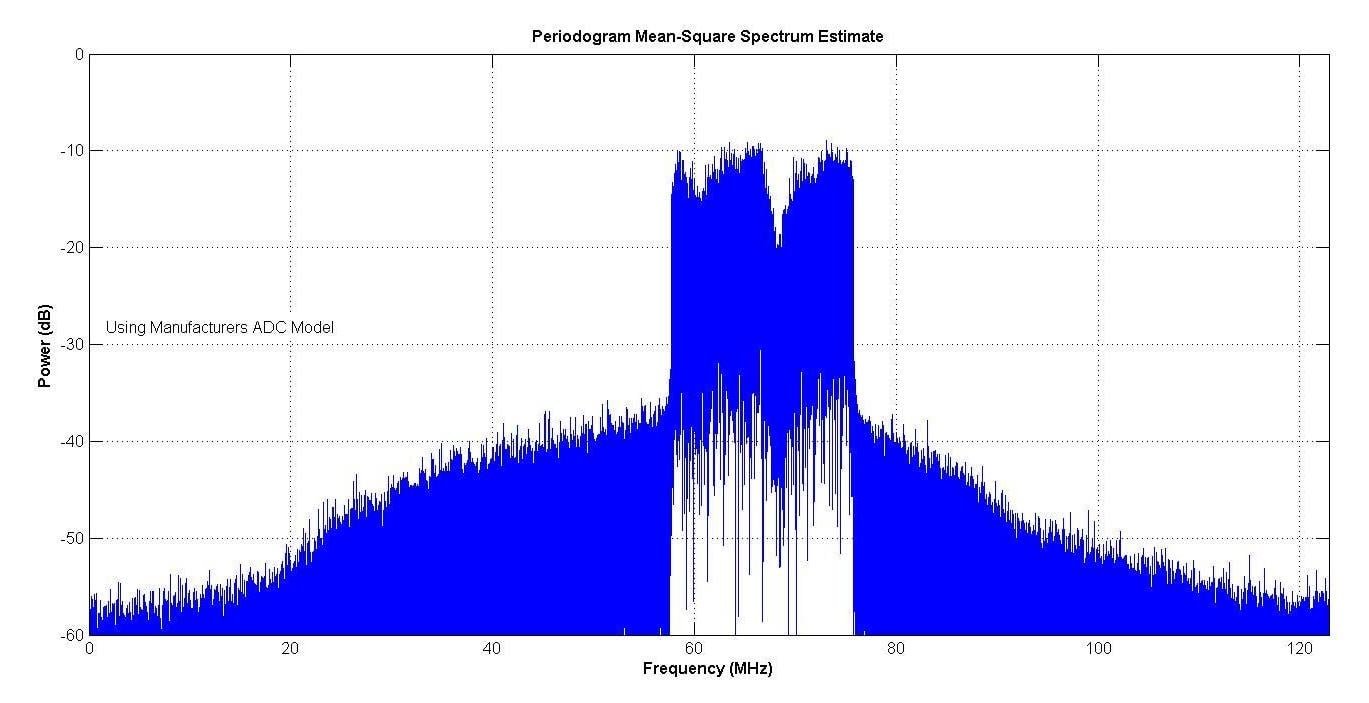
图 13.

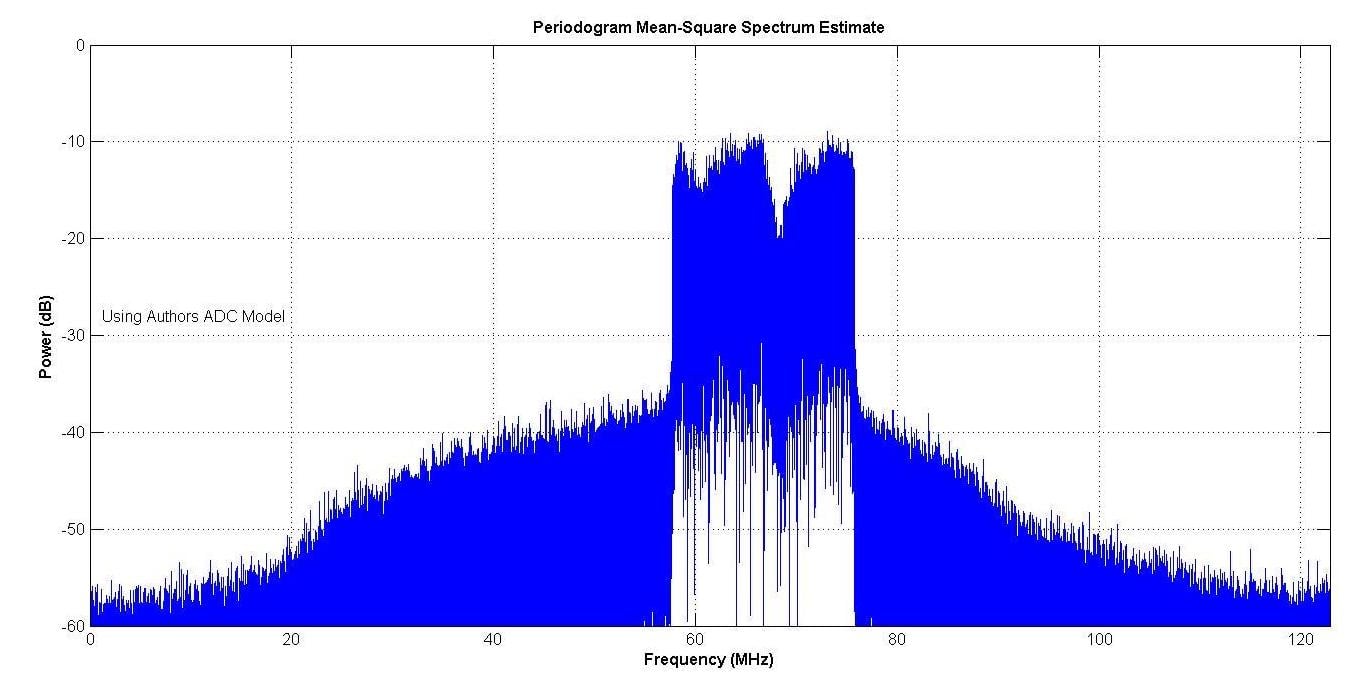
图 14.

图 15 显示了制造商型号的已接收 OFDM 星座，图 16 显示了作者模型的 OFDM 星座。

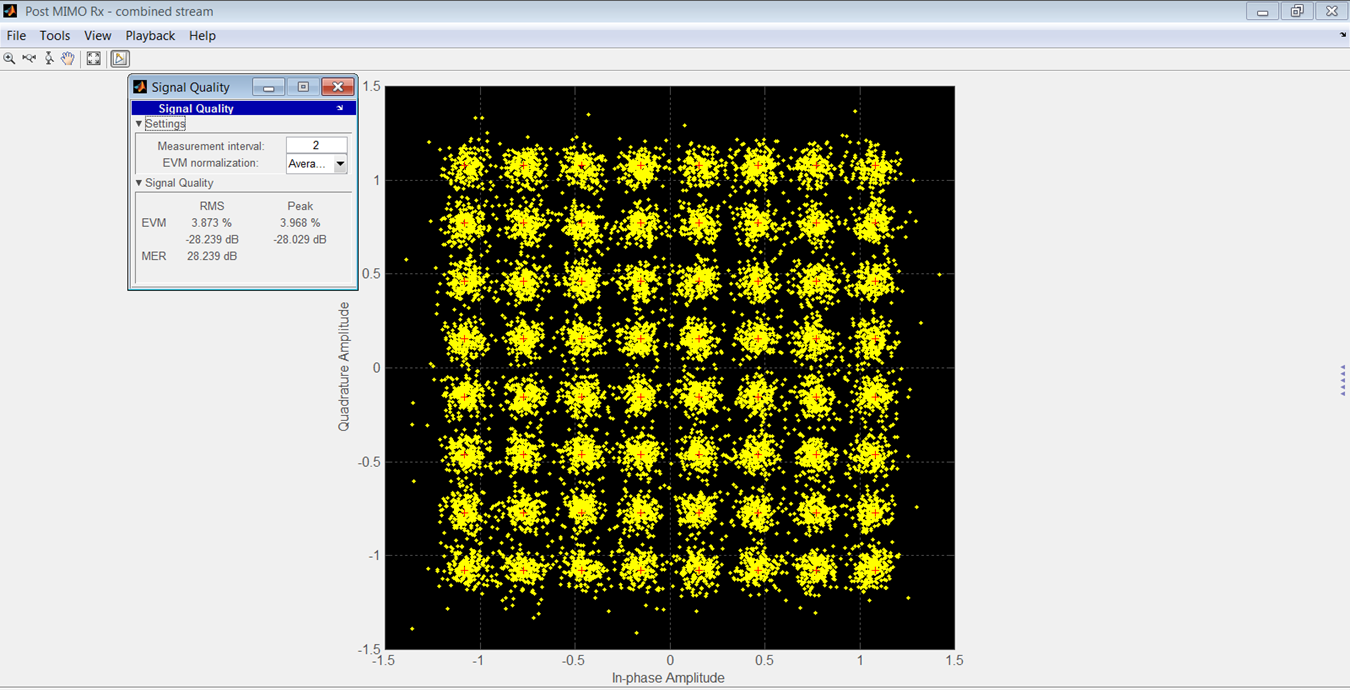
图 15.

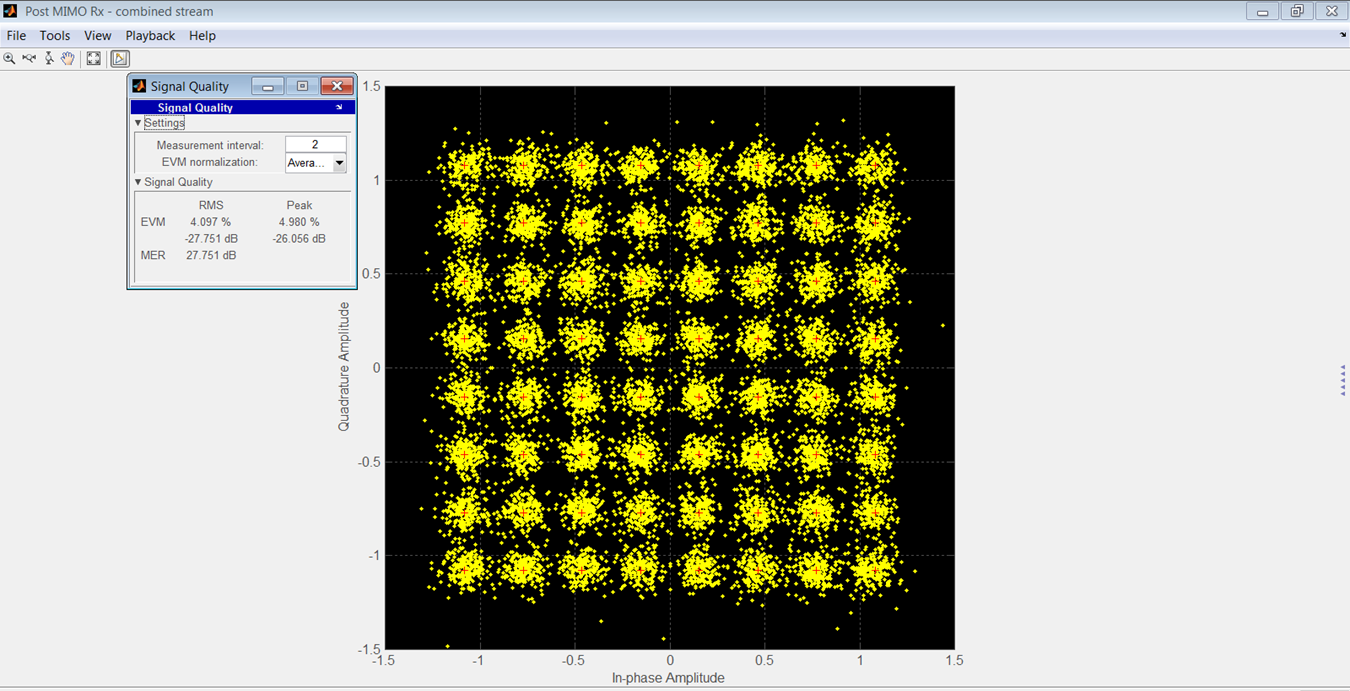
图 16.

均方根和峰值EVM的比较见表3。这些结果的信噪比为90 dB。

表 3. 

在-7至-47 dBrmsFS的范围内，两种型号的EVM之间的均方根差异为3.46 dB。

总的来说，对于一组相当简单的参数，您作者的模型给出的结果与制造商的结果非常相似。没有关于制造商型号的信息，但它可能与您作者的相似。 

无论如何，使用您作者的模型时，模拟运行得更快，因为不需要在模拟软件之间传输数据。因此，您作者的模型用于图 17 所示的误码率 (BER) 仿真。

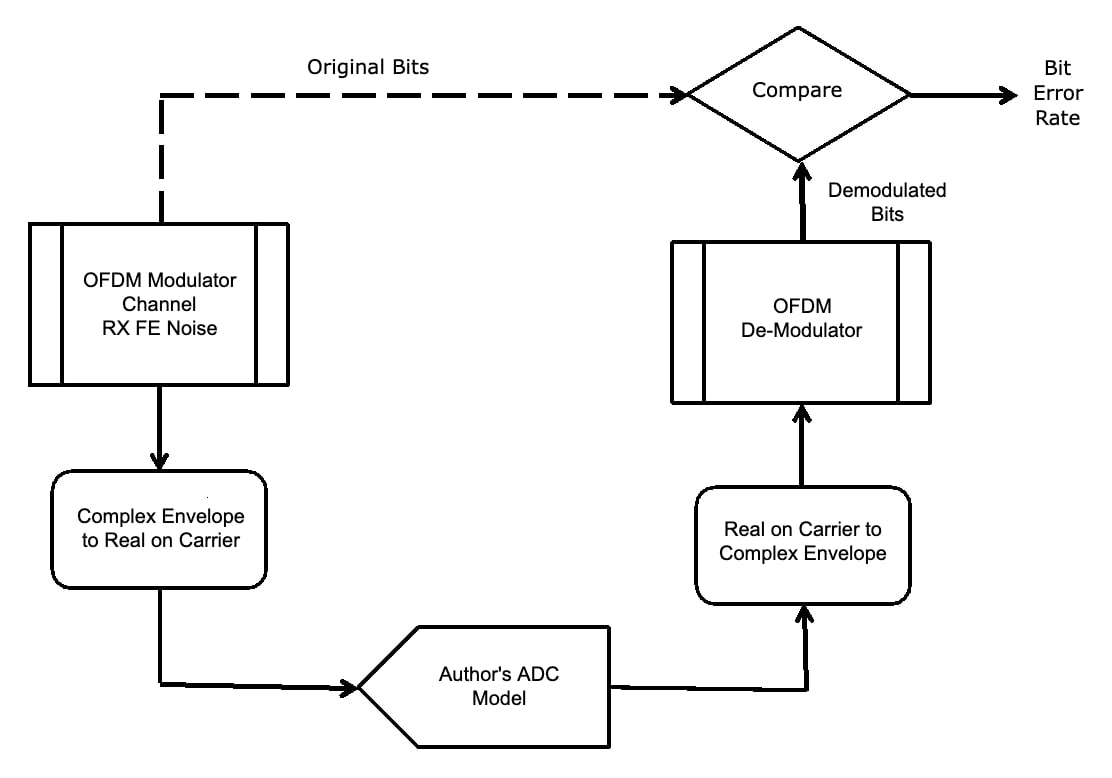
图 17。

设计带有 ADC 的系统时的一个重要参数是放置信号相对于 ADC 满量程的最佳水平。

电平太低会导致信号相对于噪声和失真而言太小。

电平太高会导致过度削波，这也会使信号失真。通常，允许一些削波的电平是最佳的。

三种不同SNR和-41至-7 dBrmsFS信号电平的误码率如图18所示。

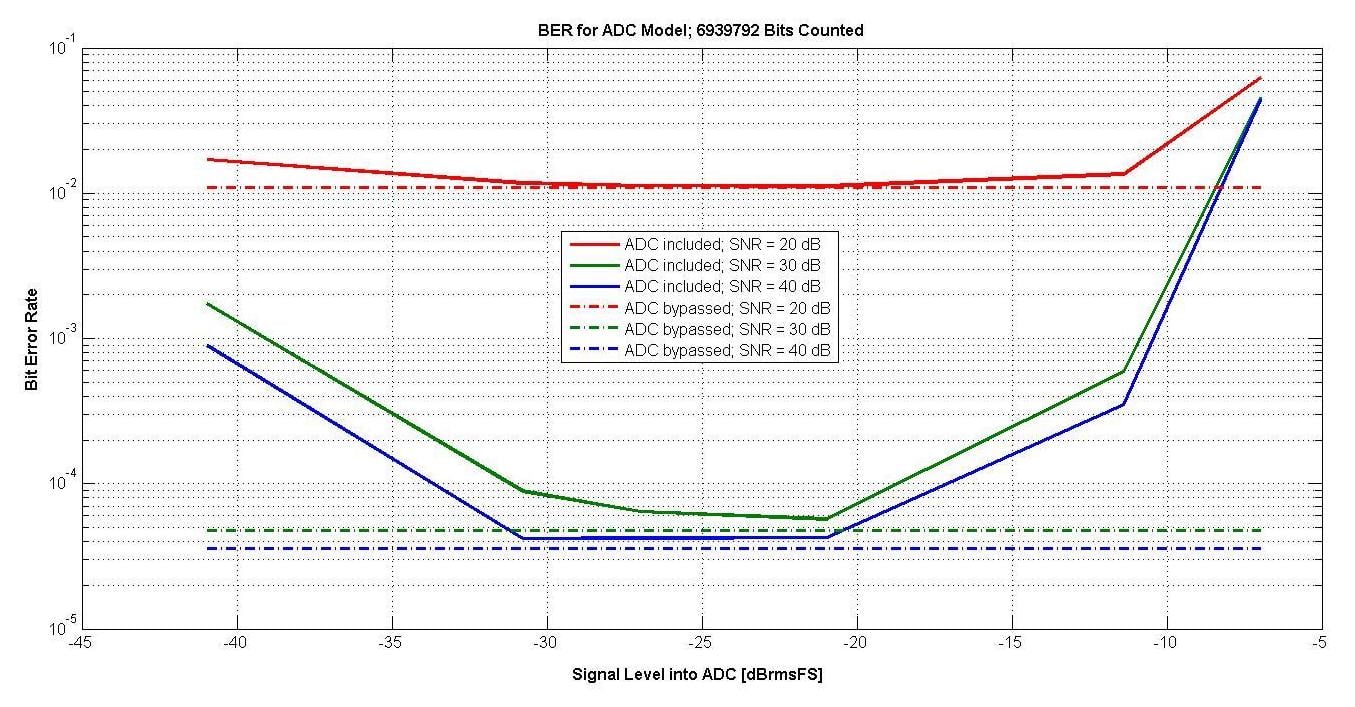
图 18.

虚线还显示了旁路ADC模型时的BER。使用ADC，最佳范围约为10 dB，自动增益控制应将信号保持在该范围内。