如何使用FFT算法分析正弦信号的频率和幅值？

当使用DAQ模块时，最常见的操作之一是对采集到的数据进行分析，其中最具代表性的操作是FFT（快速傅里叶变换）。本文将结合ChatGPT模型，演示如何使用FFT算法分析正弦信号的频率和幅值。    

 

（1）请使用C#编程，帮我实现一个生成幅值为2V、频率为1000Hz的正弦波，并将数据保存到数组中

 

以下是用C#编写生成幅值为2V、频率为1000Hz的正弦波并将数据保存到数组中的代码：

double amplitude = 2.0; // 幅值为2V

double frequency = 1000.0; // 频率为1000Hz

double sampleRate = 44100.0; // 采样率为44100Hz

double duration = 1.0; // 生成1秒钟的正弦波

int numSamples = (int)(duration * sampleRate); // 计算需要生成的样本数量

double[] samples = new double[numSamples]; // 创建用于保存生成数据的数组

for (int i = 0; i < numSamples; i++)

{

    double time = (double)i / sampleRate; // 计算当前时间

    double value = amplitude * Math.Sin(2.0 * Math.PI * frequency * time);// 计算当前样本值

    samples[i] = value; // 保存当前样本值到数组中

}

在上述代码中，我们首先定义了幅值、频率、采样率和生成时长等参数，并根据这些参数计算出需要生成的样本数量。然后，我们使用一个 for 循环逐个生成样本，并将每个样本值保存到一个数组中。

请注意，上述代码生成的正弦波数据是以浮点数形式保存的，如果需要将其存储为音频文件，需要将其转换为对应的音频格式，例如 WAV、MP3 等。

在button的Click事件中复制ChatGPT生成的代码，同时将代码生成的正弦信号显示到EasyChartX上，并手动放大，如图

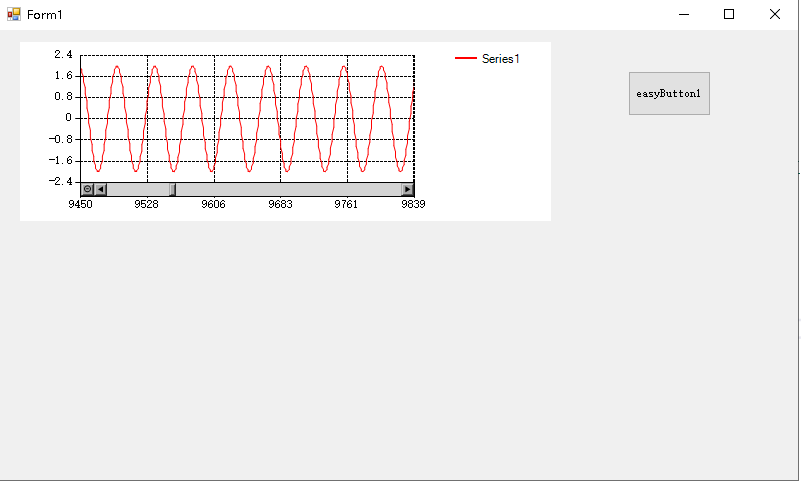
注：请使用EasyChartX的Plot方法，将数组中的数据显示在EasyChartX中，代码调用如下：easyChartX1.Plot(samples);

在上述操作中，我们将ChatGPT模型应用于生成正弦信号，为了证明生成的信号具有指定的特征，将信号绘制到EasyChartX控件上，并进行手动放大。最终的结果表明，使用ChatGPT生成正弦信号是完全可行的。

 

（2）请针对上述生成的正弦信号做FFT

 

为了对生成的正弦信号进行FFT，我们需要使用一些第三方库，例如 MathNet.Numerics。

以下是一个简单的示例代码，演示如何使用 MathNet.Numerics 库对生成的正弦信号进行FFT：

using MathNet.Numerics;

using MathNet.Numerics.IntegralTransforms;

double[] samples =// 假设已经生成了正弦波数据

// 对正弦波数据进行FFT变换

Complex[] fft = Fourier.Transform(samples);

// 计算FFT变换后每个频率的振幅

double[] amplitudes = new double[fft.Length];

for (int i = 0; i < fft.Length; i++)

{

    amplitudes[i] = fft[i].Magnitude;

}

在上述代码中，我们首先使用 MathNet.Numerics 库中的 Fourier.Transform() 函数对生成的正弦波数据进行FFT变换，得到一个包含复数的数组 fft。然后，我们通过计算每个频率的振幅来获取FFT变换后的结果，并将结果保存到一个数组 amplitudes 中。

需要注意的是，由于 FFT 变换后得到的是一个对称的频谱，因此我们只需要考虑其中一半的数据（从下标 0 到 N/2）即可。此外，由于 FFT 变换后的结果是对数级别的振幅，因此我们可能需要对结果进行对数转换或者归一化处理。

在这里ChatGPT为我们直接提供了现有的类库直接调用来对信号做FFT，那么我们可不可以让ChatGPT来帮我们生成一个FFT的算法呢？

 

（3）请避免使用各种现有的类库，请使用代码帮我生成一个FFT算法，并分别计算信号频率和幅值并显示在两textBox上

 

好的，以下是一个基于蝴蝶算法的简单FFT实现，这个算法可以对长度为2的幂次方的数据进行FFT变换，同时使用FFT算法来计算信号的频率和幅值，并将其显示在文本框。

using System;

using System.Numerics;

namespace FFTExample

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        private void btnCalculate_Click(object sender, EventArgs e)

        {

            // 将输入的字符串转换为 double 类型的数组

            double[] inputSignal = Array.ConvertAll(txtInput.Text.Split(','), Double.Parse);

            // 计算输入信号的长度

            int signalLength = inputSignal.Length;

            // 为 FFT 算法分配输入数据缓冲区

            Complex[] fftBuffer = new Complex[signalLength];

            // 将输入数据复制到缓冲区中

            for (int i = 0; i < signalLength; i++)

            {

                fftBuffer[i] = new Complex(inputSignal[i], 0);

            }

            // 执行 FFT 算法

            FourierTransform.FFT(fftBuffer, FourierTransform.Direction.Forward);

            // 计算频谱幅值

            double[] magnitude = new double[signalLength / 2];

            for (int i = 0; i < signalLength / 2; i++)

            {

                magnitude[i] = 2 * fftBuffer[i].Magnitude / signalLength;

            }

            // 计算频率

            double[] frequency = new double[signalLength / 2];

            for (int i = 0; i < signalLength / 2; i++)

            {

                frequency[i] = (double)i / signalLength * 2 * Math.PI;

            }

            // 在文本框中显示结果

            txtMagnitude.Text = string.Join(",", magnitude);

            txtFrequency.Text = string.Join(",", frequency);

        }

    }

    public static class FourierTransform

    {

        public enum Direction

        {

            Forward = 1,

            Backward = -1

        }

        public static void FFT(Complex[] buffer, Direction direction)

        {

            int n = buffer.Length;

            if (n == 1)

            {

                return;

            }

            // 分离奇偶元素

            Complex[] even = new Complex[n / 2];

            Complex[] odd = new Complex[n / 2];

            for (int i = 0; i < n / 2; i++)

            {

                even[i] = buffer[2 * i];

                odd[i] = buffer[2 * i + 1];

            }

            // 递归地计算奇偶元素的 FFT

            FFT(even, direction);

            FFT(odd, direction);

            // 合并结果

            for(int i = 0; i < n / 2; i++)

            {

                Complex t = Complex.FromPolarCoordinates(1, -2 * (int)direction * Math.PI * i / n) * odd[i];

                buffer[i] = even[i] + t;

                buffer[i + n / 2] = even[i] - t;

            }

        }

    }

}

在上述代码中，我们首先检查输入数据的长度是否为2的幂次方，如果不是则抛出一个异常。然后，我们使用递归的方式对输入数据进行FFT变换。

在每次递归中，我们首先将输入数据分为偶数项和奇数项，并递归计算它们的FFT变换。然后，我们计算每个频率的旋转因子，用它们来组合偶数项和奇数项的结果，得到最终的FFT变换结果。

需要注意的是，由于我们使用的是递归算法，因此对于较大的数据集可能会导致栈溢出，需要使用适当的技巧（例如非递归实现）来解决这个问题。

至此，ChatGPT为我们提供了FFT算法实例，该算法适用于长度为2的幂次方的数据进行FFT变换。然而，在实际应用中，我们需要确保任何情况下都可以完成FFT算法，因此需要解决FFT算法不适用于非2的幂次方数据的问题。

 

（4）若数组的长度是不是2的幂次方，该如何优化算法使其完成FFT分析

 

如果输入的数组长度不是2的幂次方，可以通过填充额外的数据使其长度成为2的幂次方，然后再对填充后的数据进行FFT变换。

一种常见的填充方式是将输入数组长度补齐到最小的2的幂次方，即将输入数组的长度n补齐到2的k次方，其中k是满足2^k >= n的最小整数。可以将额外的位置填充为0或者使用一些插值方法来填充。

填充后的数组长度为2的幂次方，可以使用上面提到的FFT算法来计算其FFT变换。计算完成后，可以仅取原始数据所占的部分，丢弃填充的0或插值的数据。

这种填充方式可能会引入一些误差，特别是当填充的数据与原始数据不太相似时，可能会导致结果的精度下降。因此，如果输入数据的长度与2的幂次方相差不大，建议直接使用快速傅里叶变换算法库，否则可以使用上述方法对输入数据进行填充。

（5）最终结果

通过ChatGPT为我们提供的算法及思路，对其完成的代码进行修改，并在Form界面上创建两个textBox和EasyChartX2，分别在两个textBox上显示通过算法计算得到的信号的频率和幅值以及在EasyChartX2显示频谱图，如下：

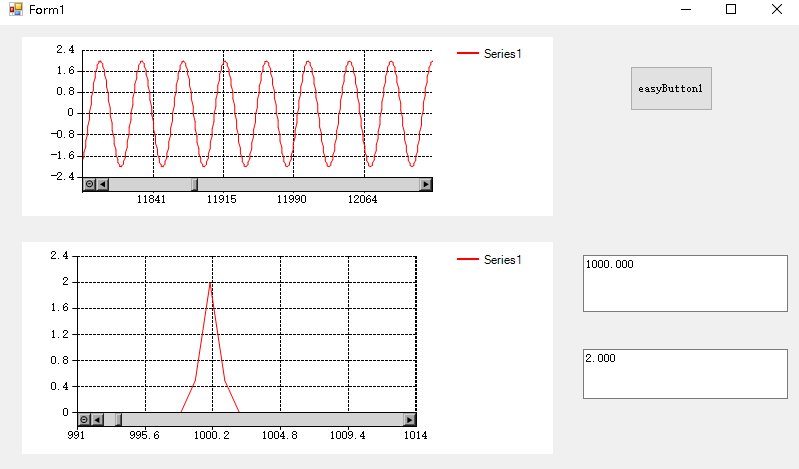
注：显示在EasyChartX上的图像是经过拖动放大后的图像

审核编辑：刘清