

数字电路基础知识分享2
电子说
描述
数字芯片本质是0-1逻辑。我们将用系列文章来一起学习数字电路基础。我们的目标不是求大求全,而是整理一些面试过程跟数字电路基础相关的知识点,以及平时工作中经常用到的数字电路知识点,大家一起学有所用,学有所成!
上节我们主要讲述了一个数值的表示方法,用进制来表示,各种进制之间的转换关系。有符号数是怎么表示的,特别是负数的原码、反码、补码表示方式。
我们说了数字电路的本质是0-1逻辑,就是通过各种逻辑操作来实现我们想要的功能。本节我们主要学习逻辑关系,以及卡诺图。
内容概括
这次为大家讲述的内容包括:
基本逻辑关系
逻辑函数及其化简(卡诺图)
0****1
基本逻辑关系
01
基本概念
逻辑常量与变量 :逻辑常量只有两个,即0和1,用来表示两个对立的逻辑状态。逻辑变量与普通代数一样,也可以用字母、符号、数字及其组合来表示,但它们之间有着本质区别,因为逻辑变量的取值只有两个,即0和1,而没有中间值。
逻辑运算 :在逻辑代数中,有与、或、非三种基本逻辑运算。表示逻辑运算的方法有多种,如语句描述、逻辑代数式、真值表、卡诺图等。
逻辑函数 :逻辑函数是由逻辑变量、常量通过运算符连接起来的代数式。同样,逻辑函数也可以用表格和图形的形式表示。
02
数字电路基本逻辑运算
与运算 : 只有当一件事情 的几个条件全部具备之后,这件事情才会发生。这种关系称与运算。逻辑表达式为 Y = AB
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
或运算 : 当一件事情的几个条件中只要有一个条件得到满足,这件事就会发生,这种关系称为或运算。逻辑表达式为 Y = A + B
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
非运算 :一件事情的发生是以其相反的条件为依据。这种逻辑关系为非运算。记作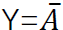
异或运算 :如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。它的逻辑表达式为 Y = A ⊕ B =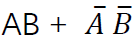
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
同或运算 :如果a、b两个值不相同,则异或结果为0。如果a、b两个值相同,异或结果为1。它的逻辑表达式为 Y = A ⊙ B =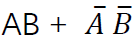
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
03
常用逻辑运算律
接下来的这些常用的逻辑运算律会在日常化简逻辑表达式上有很大帮助。
02
逻辑函数及其化简(卡诺图)
01
卡诺图的构成
卡诺图是一种包含一些小方块的几何图形,图中每个小方块称为一个单元,每个单元对应一个最小项。 两个相邻的最小项在卡诺图中也必须是相邻的。 卡诺图中相邻的含义:几何相邻性,即几何位置上相邻,世就是左右紧挨着或者上下相接;对称相邻性,即图形中对称位置的单元是相邻的。
例如:
两变量卡诺图:
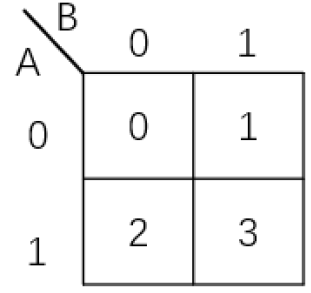
三变量卡诺图:
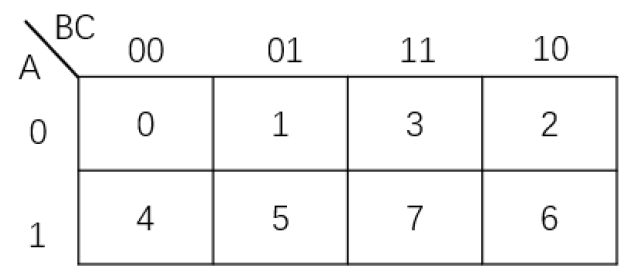
四变量卡诺图:
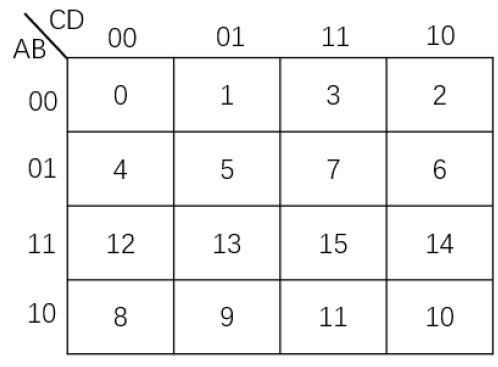
02
逻辑函数在卡诺图上的表示
l 给定逻辑函数为标准“与-或”表达式
当逻辑函数为标准“与-或”表达式时,只需在卡诺图上找出和表达式中最小项对应的小方格填上1,其余小方格填上0,即可得到该函数的卡诺图。
例如,4变量函数F(A,B,C,D)=∑m(1,5,8,9,10,13)的卡诺图如图1所示。
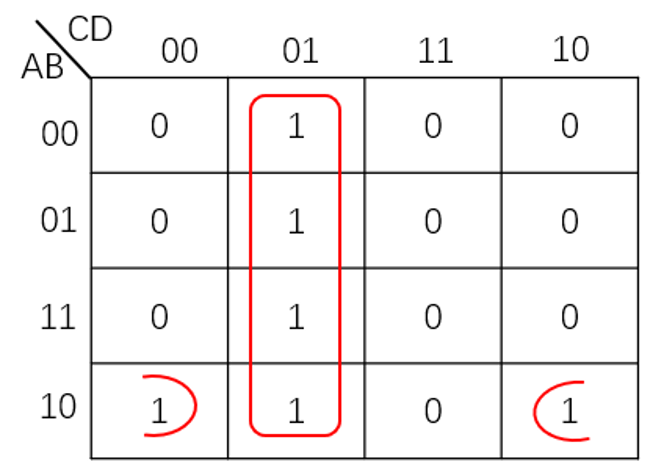
图1 函数F(A,B,C)=∑m(1,5,8,9,10,13)的卡诺图
l 逻辑函数为一般“与-或”表达式
当逻辑函数为一般“与-或”表达式时,可根据“与”的公共性和“或”的叠加性作出相应卡诺图。
例如,4变量函数F(A,B,C,D)=ABC’D+ABCD+AB’CD的卡诺图如图2所示。 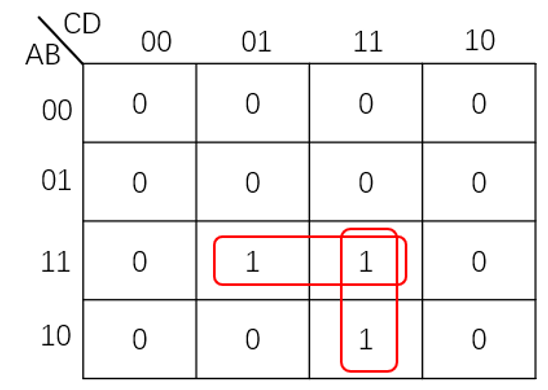
图2 函数F(A,B,C,D)= ABC'D+ABCD+AB'CD的卡诺图
填写该函数卡诺图时,只需在4变量卡诺图上依次找出和“与项”ABC'D、ABCD、AB'CD对应的小方格填上1,便可得到该函数的卡诺图。当逻辑函数表达式为其他形式时,可将其变换成上述形式后再作卡诺图。为了叙述的方便,通常将卡诺图上填1的小方格称为1方格,填0的小方格称为0方格。0方格有时用空格表示。
03
******卡诺图上最小项的合并规律
卡诺图的一个重要特征是,它从图形上直观、清晰地反映了最小项的相邻关系。当一个函数用卡诺图表示后,究竟哪些最小项可以合并呢?下面以2、3、4变量卡诺图为例予以说明。
l 两个小方格相邻, 或处于某行(列)两端时,所代表的最小项可以合并,合并后可消去一个变量。
例如,图3给出了2变量卡诺图上两个相邻最小项合并的典型情况的。
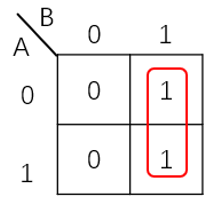
图3 两个相邻最小项合并的情况
l 四个小方格组成一个大方格、或组成一行(列)、或处于相邻两行(列)的两端、或处于四角时,所的表的最小项可以合并,合并后可消去两个变量。
例如,图4给出了4变量卡诺图上四个相邻最小项合并的典型情况的。
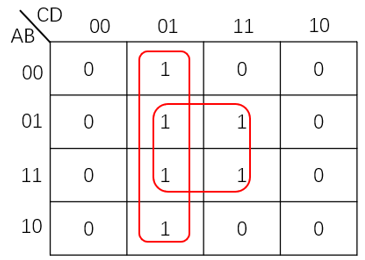
图4 四个相邻最小项合并的情况
l 八个小方格组成一个大方格、或组成相邻的两行(列)、或处于两个边行(列)时,所代表的最小项可以合并,合并后可消去三个变量。
例如,图5给出了4变量卡诺图上八个相邻最小项合并的典型情况的。
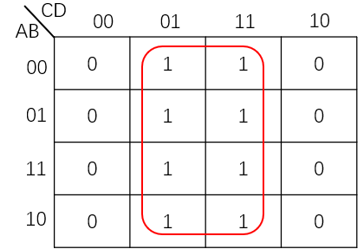
图5 八个相邻最小项合并的情况
至此,以3、4变量卡诺图为例,讨论了2,4,8个最小项的合并方法。依此类推,不难得出n个变量卡诺图中最小项的合并规律。
归纳起来,n个变量卡诺图中最小项的合并规律如下:
(1)卡诺圈中小方格的个数必须为2m个,m为小于或等于n的整数。
(2)卡诺圈中的2m个小方格有一定的排列规律,具体地说,它们 含有m个不同变量,(n-m)个相同变量 。
(3)卡诺圈中的 2m个小方格对应的最小项可用(n-m)个变量的“与”项表示 ,该“与”项由这些最小项中的相同变量构成。
(4) 当m=n时,卡诺圈包围了整个卡诺图,可用1表示 ,即n个变量的全部最小项之和为1。
04
******卡诺图化简逻辑函数
首先,有这么几点需要明确:
l 列出逻辑函数的最小项表达式 ,由最小项表达式确定变量的个数(如果最小项中缺少变量,应按例的方法补齐)。
l 画出最小项表达式对应的卡诺图。
l 将卡诺图中的1格画圈。 一个也不能漏圈,否则最后得到的表达式就会与所给函数不等;1格允许被一个以上的圈所包围。
l ** 圈的个数应尽可能得少。**即在保证1格一个也不漏圈的前提下,圈的个数越少越好。因为一个圈和一个与项相对应,圈数越少,与或表达式的与项就越少。
l 按照2k个方格来组合(即圈内的1格数必须为1,2,4,8等),圈的面积越大越好。 因为圈越大,可消去的变量就越多,与项中的变量就越少。
l 每个圈应至少包含一个新的1格,否则这个圈是多余的。
l 用卡诺图化简所得到的最简与或式不是唯一的。
例子:
用卡诺图化简法化简下式为最简单与或逻辑式
Y = ABCD+ BCD + BD
首先可先把他化成最小项之和的形式:
Y = ABCD + (A + A’)BCD + (A + A’) B (C + C’) D
然后我们例如卡诺图,将可能合并的最小项圈出,并按照前面所述的原则进行化简后与或式中的乘积项,于是我们得到化简后的表达式:
Y = BD
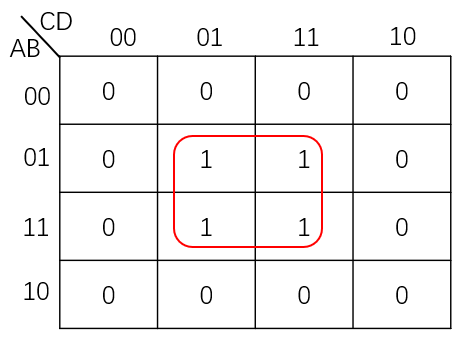
-
电路基础知识总结2023-08-30 5821
-
电路基础知识讲解 电路基本元件知识与电路元件的伏安特性和功率特性2023-07-31 5802
-
数字电路基础知识分享12023-05-04 1848
-
17个图解数字电路基础知识2023-01-14 17765
-
数字电路基础2022-03-21 1939
-
电路基础知识分享2022-03-10 2029
-
数字电路基础知识相关资料下载2021-12-01 2539
-
直流电路基础知识2021-09-15 1708
-
数字电路基础知识与要点2017-09-19 1728
-
磁路和电路基础知识2017-04-07 2456
-
数字电路基础知识2011-04-01 5242
-
模拟电路基础知识教程2009-12-04 41703
-
电子电路基础知识2008-01-15 247833
全部0条评论

快来发表一下你的评论吧 !

