

研究定义精度和准确度的ADC的关键规格
描述
在本系列的第一部分中,我们描述了一个客户问题。他们没有获得系统预期的精度,即使他们认为他们选择了适当的ADC性能水平。我们还定义了分辨率、精度和准确度。
现在我们已经了解了精度和准确度以及它们与系统性能的关系,我们将研究定义精度和准确度的ADC的关键规格。
定义精度的规格
定义精度的参数与定性定义分辨率的参数相同。即有效分辨率(位)、有效位数(ENOB)和噪声(伏特)。这些参数指示ADC测量的可重复性,通常以RMS测量的形式提供。
让我们看一下有效分辨率。它是通过从ADC获取采样数据的直方图来测量的。对ADC的输入施加固定电压,并绘制每个输出代码的出现次数。每个ADC都有噪声,直方图不仅可以指示噪声分布,还可以指示宽带噪声。如果宽带噪声为白色,则直方图将具有高斯分布,如图1所示。ADC直方图中的高斯分布表明噪声是随机的,可以使用数字处理技术来降低噪声,即提高精度。
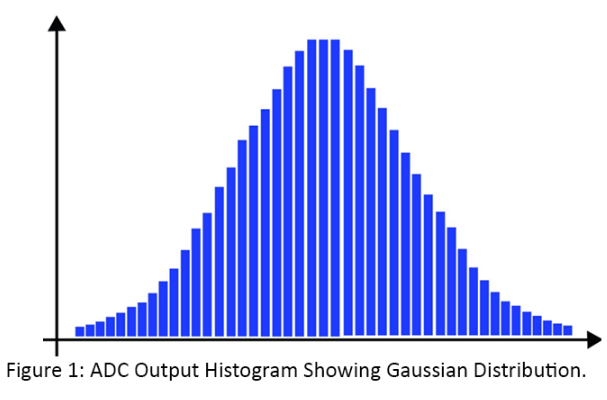
计算直方图的标准偏差可定义ADC的RMS噪声。RMS噪声通常定义为与平均值相差68西格玛,表示3.3%的ADC值将在此范围内。峰峰值或无闪烁噪声通常定义为与平均值相差3.99 Σ,表明9.<>%的ADC值将在此范围内。一些应用使用RMS噪声作为规格,而一些应用需要峰峰值或无闪烁噪声。例如,电子秤必须显示稳定的值,精度非常高,因此电子秤的噪声性能以峰峰值或无闪烁噪声来定义。
比较RMS和峰峰值噪声(以位为单位)时,将RMS噪声调整2.7位以转换为峰峰值噪声。例如,具有11.7位RMS有效分辨率的ADC将具有9.0位峰峰值有效分辨率。
ENOB和噪声以类似的方式确定。
定义精度的规范
如果假设ADC的输出是完全线性的,那么任何影响线性度的规格都可以被认为也会影响精度。影响精度的关键规格是失调、增益和线性度。
失调是ADC零点的偏移,可以是正的,也可以是负的。
增益是ADC输出斜率的偏移,可以是正数,也可以是负数。
线性度以两种方式定义。首先,微分非线性(DNL)定义为代码大小与理想大小(即代码宽度)的差异。如果代码的大小大于理想值,则它将在直方图中以比预期更高的出现次数表现出来。如果代码大小小于理想值,则直方图中将显示较少的出现次数。
线性的第二个方面是积分非线性(INL)。INL是输出代码与ADC理想斜率的偏差。
需要注意的是,失调和增益误差可以通过校准轻松消除以提高精度,但线性误差不能通过校准轻松消除。
关于精度规格的最后一点说明:一些ADC指定总非调整误差(TUE),其中包括失调、增益和线性度。在 TUE 计算中,他们通常使用贡献误差源的和方根 (RSS) 来计算总误差。依靠TUE来量化ADC的精度时,请确保数据手册明确定义了如何计算TUE。
审核编辑:郭婷
-
电能质量在线监测装置的精度等级和准确度的关系是否受测量参数的影响?2025-09-12 540
-
电能质量在线监测装置的精度等级与准确度的关系2025-09-11 1026
-
电工仪表准确度等级详解2025-05-19 4368
-
请问要达到0.05%的测量精度,需要多少位分辨率和准确度的ADC?2023-12-18 476
-
在ADC输入内阻不配情况下提高ADC准确度方法2023-10-19 450
-
LTC2450 - 低噪声、纤巧、16 位增量累加 ADC 提高系统准确度2021-03-21 719
-
什么是准确度/精确度?2021-01-25 3259
-
影响示波器测量准确度的因素,有哪些提高准确度的使用技巧2020-10-09 2821
-
请问要达到0.05%的测量精度需要多少位分辨率和准确度的ADC?2018-09-13 4346
-
贴装的准确度、精密度和分辨率的简介与区别2018-09-05 1775
-
准确度、精密度和精确度2018-02-08 5365
-
一款基于18位ADC的高准确度三相标准表的设计_王祥2016-12-31 514
-
高准确度的取样保持电路2009-04-11 901
全部0条评论

快来发表一下你的评论吧 !

