

FPGA无限通信技巧—位交织
描述
FPGA无限通信技巧—位交织
当调制方式为16-AQM,64-QAM和256-QAM时需要做位交织,交织的目的是将突发的错误分散开来,把一个较长的突发差错离散成随机差错,再用随机差错的编码(FEC)等信道编码技术消除随机差错,提高通信的可靠性。交织的越深,抗突发错误的能力也越强。位交织的本质是做矩阵的转置运算,需要转置的数据包括信息位和校验位,在交织的过程中分两步完成,步为检验位交织,第二步为列旋转交织。
1.QAM调制方式介绍
QAM正交振幅调制,其幅度和相位同时变化,属于非恒包络二维调制。它把2ASK和2PSK两种调制结合起来,使得带宽得到双倍扩展。ASK和PSK调制方式如下图所示:
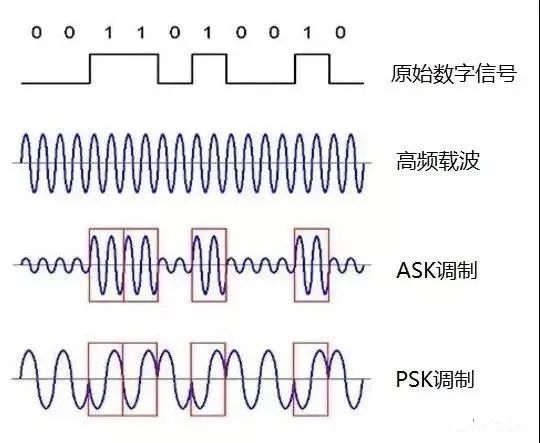
QAM调制技术用两路独立的基带信号对频率相同、相位正交的两个载波进行调幅,并将已调信号加在一起进行传输。nQAM代表n个状态的正交调幅,一般有二进制(4QAM)、四进制(16QAM)、八进制(64QAM)、十六进制(256QAM)。得到多进制的QAM信号,需要将二进制信号转换为m电平的多进制信号,然后进行正交调制,相加输出。
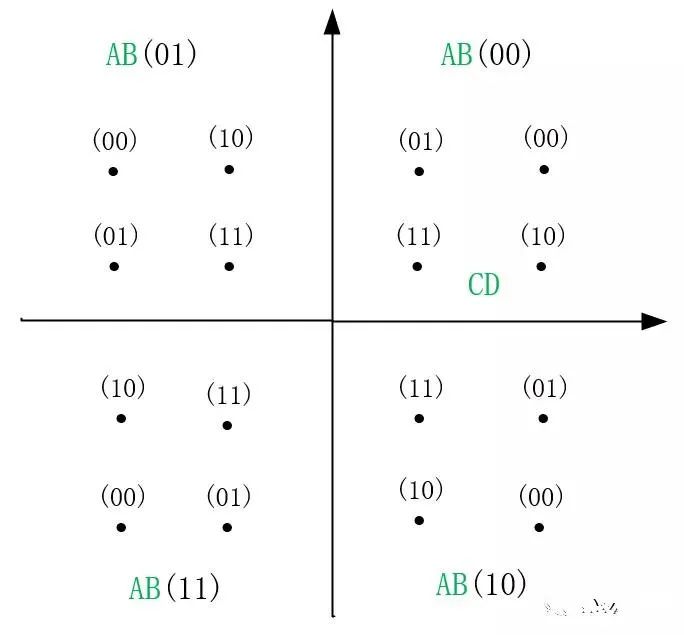
通信系统中通常把信号矢量端点的分布图成为星座图,同眼图相比,星座图可以看成数字信号的一个二维眼图阵列,屏幕上的图形对应着幅度和相位,通过星座图,可以发现诸如幅度噪声,相位噪声,相位误差等调制问题,采用格雷码编码技术,16QAM星座图编码映射关系如下图所示:
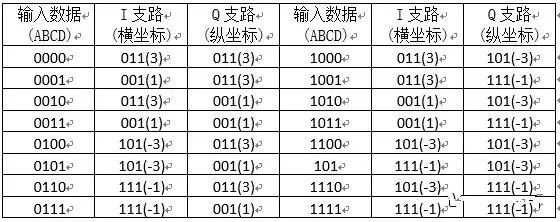
横纵、坐标的取值均有4种,分别为±1、±3,每种坐标需要3bit二进制来表示,差分编码后输入的符号与QAM调制系统中的I、Q之路幅值映射关系如下表所示:
2. 检验位交织
检验位进行交织的时候,信息为的数据需要保持不变,检验位交织需要满足以下方程:
根据校验位交织地址生成公式可知,交织前的矩阵为Qldpc*360,即依次向数据每行写入360个数,第361个数为第二行列数,依次类推。存放Rom地址如图所示:
交织的本质是行进列出,即取数据依次如下地址取数据,重新生成新的一组向量Matlab 中,重新产生读数据的地址索引,即可实现矩阵的转置,使用两个for循环在硬件平台上实现上述操作则需要两个计数器来实现地址的累加,实现的波形如图所示3. 列旋转交织
校验位交织输出ui按列顺序依次写入列旋转交织器,然后按行依次读出,完成列旋转交织,每列写入的起始位置由tc决定,整个旋转交织见下图列旋转交织用公式表示如下:
输入为ui,0≤i≤Nldpc,写入交织器的ci列,ri行,其中列旋转交织器的输出为ui,0≤i≤Nldpc,从交织器的ri行,ci列读出,其中列旋转交织测参数为Nldpc = 16200,Rows Nr =2025,Columns Nc = 8,列旋转参数tc见下表交织之前的数据地址为
对于列旋转交织,每列Tc的值都是确定的,因此可以按照一定规律求出每列的地址,如下图所示,以第四列Tc为7为例,即数据整体往后移7行,7行的数据,移到前面的几行。求出新的地址后,依次将行地址数据读出即完成位旋转交织。
在计算列旋转交织的时候需要考虑固定延迟Tc,在matlab中,可以这样得到交织的结果相比奇偶校验,列旋转交织多了Tc的延迟,需要在正常产生地址的情况下再进行操作,正常地址产生的操作同奇偶校验。Tc是21,因此可以定义一个状态机来完成此操作,如下:
对照交织之后得到的地址矩阵,在状态Row_1读取行的地址,前三列Tc =0,不做任何操作,正常读出转置后的地址即可;第四列需要加上2025-1,第五列加2025-7,后面的三列也按照Tc的延迟进行操作。Row_2代表第二行,依次类推,读完21行之后,相同的列对应的操作都一样,都在Row_last中完成Gen_end表示交织完成,跳转到状态0,等待下一帧的操作。
从以往的学习经验来看,想从新手进阶为FPGA高手、行业资深FPGA开发工程师,您不仅要学习基础的数字电路知识,掌握基础电路如组合逻辑、时序逻辑电路的原理与实现方法。编程语言方面,学会使用硬件描述语言Verilog或者VHDL,并选择相应FPGA开发平台设计软件(Quartus或者ISE),找相关的实例“抄写”代码,逐渐熟悉FPGA硬件语言编程及编译器使用。经过前面一段的铺垫学习,然后你就可以自行尝试设计数字电路了。在做项目的时候,根据提供时序图使用HDL语言去完成它,这时候你就可以购买FPGA开发板去完成项目后续设计、验证和sim仿真设计了。
审核编辑 :李倩
-
FPGA无限通信技巧—位交织2023-05-06 1503
-
FPGA如何使用RAM分区循环移位法实现解交织器2021-09-28 3475
-
[Mill]无线通信连载——交织2020-01-08 6824
-
基于FPGA的交织编码技术研究及实现2018-05-11 4016
-
求一个Verilog HDL ***数据交织/解交织器的代码2016-07-03 5391
-
TURBO码实时交织器的FPGA实现2010-08-06 1166
-
可变参数交织编码器的FPGA实现2010-07-28 1010
-
IDMA通信系统中的粒子群交织算法2009-12-19 1772
-
地面数字视频广播中内交织器与解内交织器设计2009-12-14 705
-
基于FPGA的改进型分组交织器的设计与实现2009-11-06 1665
-
利用FPGA技术实现数字通信中的交织器和解交织器2009-06-20 1574
-
一种交织器和解交织器的FPGA电路实现2009-02-08 1909
-
为什么要进行交织处理?什么是分组交织?什么是卷积交织?2008-05-30 20028
全部0条评论

快来发表一下你的评论吧 !

