聊聊振荡电路、功放电路等结构和工作原理

实用的无线发射电路应包括正弦波振荡电路、调制电路、高频功率放大电路和天线。

本章逐一讨论振荡电路、功放电路、天线等单元电路结构、工作原理和特性，调制电路在第3章讨论。

一、正弦波振荡电路组成

X0-输出正弦波电压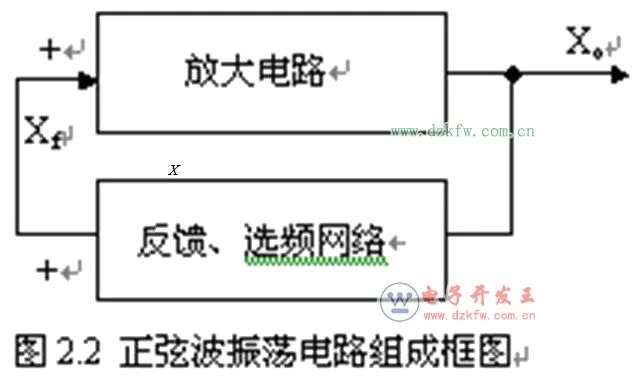

Xf-反馈电压,即放大电路的输入电压

接下来推导正弦波振荡的平衡条件

电路达到稳定后（即振荡电路有稳定的输出）应有：

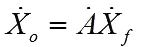
反馈电压等于：

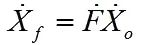
由此求得：

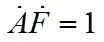
称为正弦波振荡的平衡条件，表明正弦波振荡电路形成稳定输出后，放大电路的放大倍数和反馈网络的反馈系数的乘积等于1。

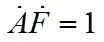是相量式 两边的模应该相等，求得!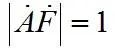称为幅值平衡条件

两边相位也应该相等，得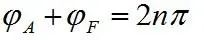称为相位平衡条件

根据上述两个平衡条件可以导出正弦波振荡电路产生稳定输出所需要满足的3个条件：

**（1）起振条件 **

振荡电路接通电源以前以及刚接通电源时的输出为零，这表明振荡电路输出电压从零变化到稳定值有一个逐渐升高的过程，这个过程即为振荡电路的起振。

起振过程中，输出电压不断升高，反馈系数和放大倍数幅值的乘积就应该大于1，即

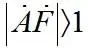称为振荡电路起振条件。

既要满足平衡条件，又要满足起振条件，有矛盾吗？

放大倍数A是一个随工作状态变化的量，起振时，放大电路工作于线性区，A的数值较大，随输出电压的增加，进入非线性区域后，A的数值随放大电路输出信号振幅变化，振幅变大，A变小，稳定时A满足平衡条件，振幅趋于稳定。

（2）形成正反馈

相位平衡条件式满足时，振荡电路的反馈电压就会形成正反馈

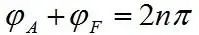
假设初始时刻放大电路输入电压的极性为“正”，如图，经过放大电路，产生相位移动φA，经过反馈网络又产生相位移动φF，因此所形成的反馈电压与初始输入电压之间的相位差等于φA+ φF，根据相位平衡条件，两者之和等于2π的整数倍，这表明反馈电压和初始电压相位相同，因此振荡电路所形成的为正反馈。

**（3）必须有一个选频的环节 **

按照相位和振幅平衡条件，各种不同频率的信号都可能在输出端形成稳定的输出，这样一来，振荡电路输出的就不是正弦波电压，而是各种频率合成的振荡信号。

为了获得正弦波电压输出，就必须有一个选频的环节。

高频电子技术中用到多种选频电路，我们以LC谐振回路为例进行说明。

LC并联电路的特性曲线如下图，(a)是LC并联电路，(b)是幅频特性曲线，(c)为相频特性曲线。

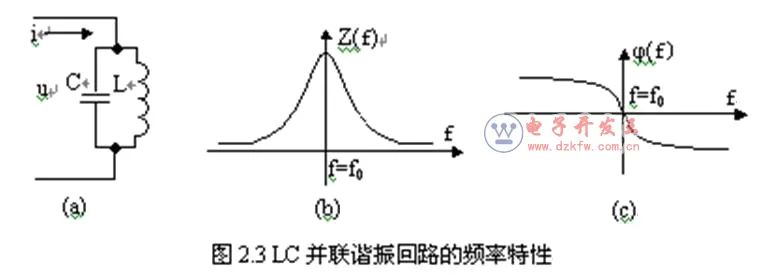
(b)表示输入信号频率等于谐振频率f0时，回路表现为很高的阻抗：

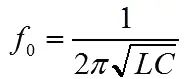
用LC回路组成反馈选频网络

图中只有频率等于f0的正弦波信号才在LC回路两端形成最大的输出电压，对其他频率的信号，LC回路是低阻抗，建立不起高的电压，因此输出端得到的就是频率等于f0的正弦波电压。

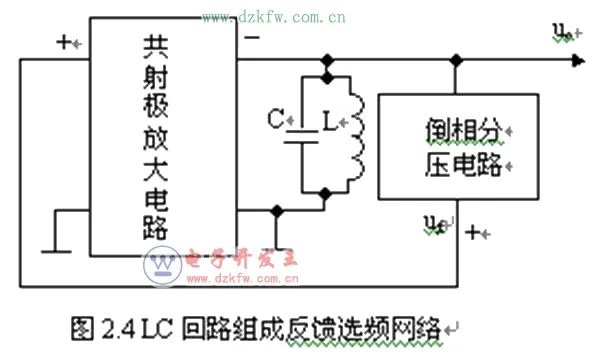
反馈电压取自输出电压并进行倒相，形成的是正反馈

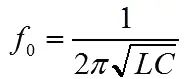
二、正弦波振荡电路主要性能指标

高频电子技术中主要通过以下三个指标来衡量正弦波振荡电路的优劣。

1、振荡频率

高频电子技术所涉及的振荡频率都比较高，例如在获得广泛应用的甚高频至特高频段，无线电波的频率在30MHz至3000MHz之间。某种振荡电路能否获得应用，决定于这个电路能否产生如此高频的正弦波电压输出，因此振荡电路的振荡频率自然就成为电路的重要特性指标。

2、振荡频率的稳定度

振荡电路的频率稳定性常用稳定度表示。若振荡器频率为f0，由于温度变化等原因发生了Δf的变化，则用（Δf/ f0）×100%来表示稳定度。实用上，频率稳定度又分短期稳定度和长期稳定度。频率的突变一般由电源电压或外界干扰变化引起，缓慢的频率变化，则由环境温度变化、元件参数变化所致。因此，表示振荡电路稳定度时，有时用（Δf/ f0）/时，即一小时内频率变化百分之几；有时也用（Δf/ f0）/月，即一个月内频率变化百分之几。

3、振荡频率的可调节性

无线通信时，收发电路的频率必须相等才会有较好的通信效果。在生产时却很难做到这一点，完全相同的设计图纸所生产出来的发射或接收电路的频率也可能有较大的差异。如果振荡电路的频率可以通过某个元件，例如可变电容来调节，就可以方便地使发射电路和接收电路的频率相等。可见，一个振荡电路的频率是否可调、调节范围多大、调节是否方便等也是振荡电路的重要指标之一。

三、振荡电路的分类

常用的正弦波振荡电路有以下5类，其中RC振荡电路频率过低，高频电路中不使用，本章首先介绍LC振荡电路、石英晶体谐振器振荡电路和声表面波谐振器振荡电路。陶瓷谐振器组成的正弦波振荡电路将在下一章介绍。

（1）RC振荡电路

（2）LC振荡电路

（3）石英晶体振荡电路

（4）声表面波谐振器振荡电路

（5）陶瓷谐振器振荡电路